こんにちは、 家庭教師のあすなろスタッフのカワイです。
今回は負の数を含んだかけ算のやり方について解説したいと思います。
負の数を含んだかけ算は小学校の頃のように、物が増えていくという考え方での説明は難しいです。なので、今回は速さ×時間=道のり(距離)という考え方から解説していきます。
これからは、掛け算の事を「乗法」といいます。そしてその答えを「積」といいます。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
速さ×時間として考えてみる
とある人が一方向(右か左)へずっと歩き続けているとして、数え始めの位置を0とします。+〇を毎秒右に〇進むこととして(-〇は毎秒左に〇進むこととして)、その時に、+△を△秒後(-△を△秒前)とします。
(正の数)×(正の数)
では仮に、2×2を考えてみましょう!
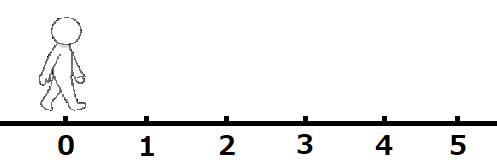
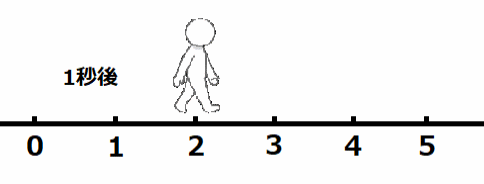
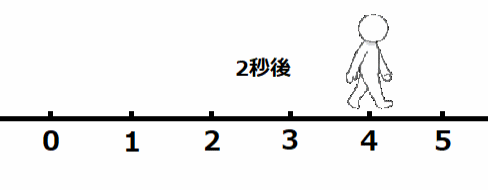
毎秒右に2進む人の2秒後はどこにいるかというと、上の図のように、右に4進んだところにいます。
従って、2×2=4です。小学校で勉強したかけ算と同じなので、正しいという事が分かってもらえると思います。
当然ながら、(正の数)×(正の数)=(正の数)となります。
(正の数)×(負の数)
さて、同様に、2×(-2)を考えてみましょう!
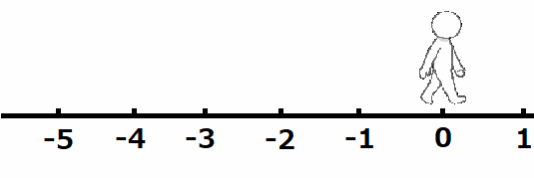
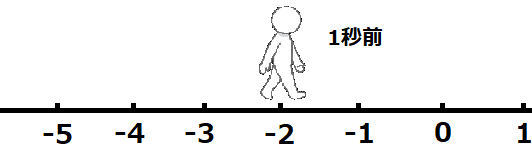
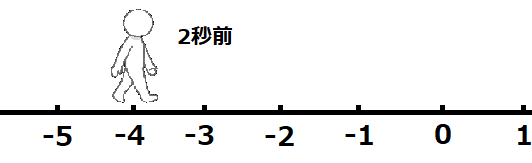
1秒で右に2進んでいるという事は、1秒前には左に2のところにいると考えられますね。となると、2秒前は左に4の位置にいると考えることができます。0より右を正としているので、左に4は-4と表せます。従って、2×(-2)は-4となります。
これより、(正の数)×(負の数)=(負の数)という事がいえます。
(負の数)×(負の数)
では、(-2)×(-2)ではどうなるでしょうか。-2・・・すなわち左に毎秒2進んでいる人の、数え始めから二秒前の位置はどこなのか、という問題だと解釈できます。ついてこれていますか…?
さて、数直線上に出してみましょう。
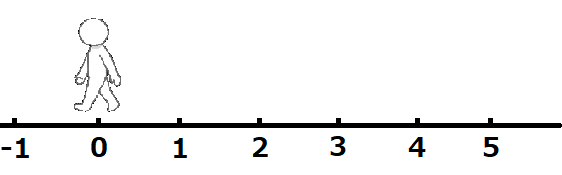
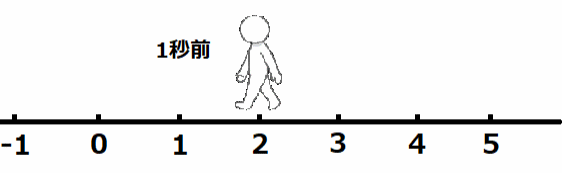
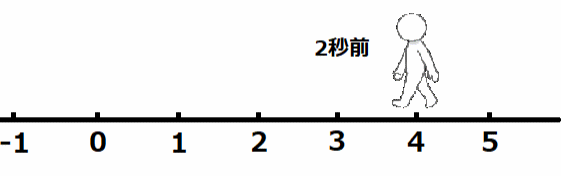
1秒で左に2進むので、1秒前は右に2の位置にいると考えることができます。よって、2秒前は右に4の位置にいると考えられます。よって、(-2)×(-2)=4となります。
これより、(負の数)×(負の数)=(正の数)という事が言えます。
3つ以上の項の乗法
項を拡張していきましょう。3つ以上の項の乗法では、符号について考えれば、あとは小学校で学んだかけ算と同じになります。
例として、いくつか式を挙げてみます。
\(3×(-2)×2=-12\)
\((-2)×2×(-4)×2=32\)
\((-5)×(-1)×(-3)=-15\)
\((-2)×(-3)×(-4)×(-1)=24\)
これらの式と積は上から負の項を1~4に増やしていったものになりますが、何か気付くことはありませんか?
そうです。負の項が1,3個の時は積が負となり、負の項が2,4個の時は積が正となっているのです!これらより、このようなことが分かります。
- 負の数が奇数個のとき積は負(-)になる
- 負の数が偶数個のとき積は正(+)になる
まとめ
いかがでしたか?物の数での考え方では、上のような負の数を含んだ計算は難しいと思いますが、時間と速さという考え方にすれば、意外とすんなりと受け入れられるのではないでしょうか。
肝心の計算の方は、積の符号さえ間違えなければ、小学校の掛け算と同じように簡単に解くことができます。もし周りに考え方が分からなくて困っている人がいたら、教えてあげてくださいね!
やってみよう!
問題
次の積を求めましょう。
- \((-2)×(-3)\)
- \(4×(-5)\)
- \((-3)×3×4\)
(計算の順序は、①~③ で求めることが出来ます)
- 負の項の数を数えて、積の符号を判別する
- 符号を無視して計算する(絶対値同士の掛け算をする)
- 計算結果に積の符号を付ける
答え
- 負の項が2つだから、積は正になる \(2×3=6\)なので、\((-2)×(-3)=6\)
- 負の項が1つだから、積は負になる \(4×5=20\)よって\(4×(-5)=-20\)
- 負の項が1つだから、積は負になる \(3×3×4=36\)よって、\((-3)×3×4=-36\)
最後までありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば嬉しいです。

























































