数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。今回は高校1年生の数学の中でも集合と論理について書いていきたいと思います。集合と論理の内容は数学はもちろん、他の教科の問題を考えるときに使ったりもします。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
集合とは
集合とは「属するか属さないかが明確に判別できるものの集まり」のことで、大文字のアルファベットで表されます。
必ず身に付けないといけないこと
集合という分野では、新しい記号がたくさん出てきます。記号が何を意味しているか分からないと全く問題が解けないのでまずは記号が何を意味しているかとよく使う法則を紹介していきたいと思います。
記号
ここでは基本的な6つの記号を紹介していきます。
①要素\(a∈A\)
集合を構成する1つ1つの対象のことを「要素」といいます。
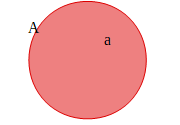
要素aが集合Aに属している時、\(a∈A\)と表します。
下の図のように、aという要素がAという集合の中に含まれている状態のことを表しています。
②部分集合\(B⊂A\)
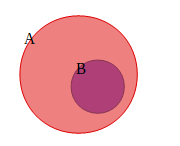
集合Bが集合Aに含まれている時、「BはAの部分集合」であるといい、\(B⊂A\)と表します。下の図のように、Bという集合がAという集合の中に含まれている状態のことを表しています。
③共通部分\(A∩B\)
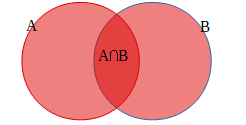
AとBの両方に属する要素全体の集合を「AとBの共通部分」といい、\(A∩B\)と表します。
下の図でAとBが重なって色の濃くなっている部分が共通部分です。
④和集合\(A∪B\)
AとBの少なくとも一方に属する要素全体の集合を「AとBの和集合」といい、\(A∪B\)と表します。下の図で色のついている部分が和集合です。

⑤空集合 \(Φ\)
要素を1つも持たない集合のことを空集合といいます。空集合はすべての集合の部分集合です。
⑥補集合\(\bar{A}\)
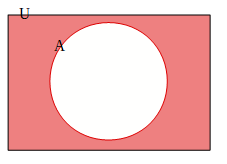
全体集合をUとして、AをUの部分集合としたとき、集合Aに属さない集合Uの要素全体の集合を「UにおけるAの補集合」といい、\(\bar{A}\)と表します。補集合を考えるときはどの集合の中の話なのかに注意する必要があります。下の図で色のついている部分が UにおけるAの補集合です。
法則
①ドモルガンの法則
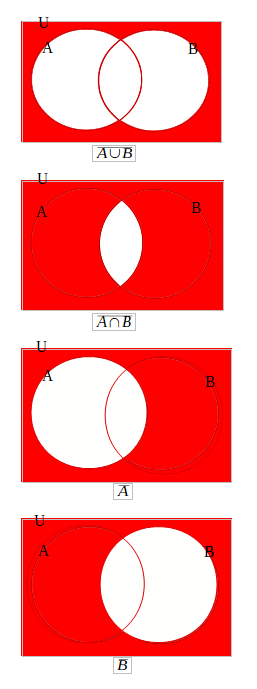
集合で一番有名な法則は「ドモルガンの法則」で、以下のような式で表すことができます。式が合っているかどうかは図で考えると分かりやすいですよ。
I .\(\bar{(A∪B)}=\bar{A}∩\bar{B}\)
II.\(\bar{(A∩B)}=\bar{A}∪\bar{B}\)
②2つの集合の和集合
2つの集合の和集合を考えるときによく使う法則です。特に名前がついているわけではありませんが、よく使うので抑えておいた方がいいですよ。
式で表すと
\(n(A∪B)=n(A)+n(B)-n(A∩B)\)
という式で表せます。
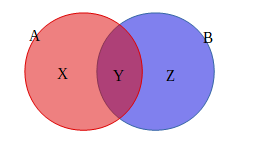
上の図で考えると、
\(n(A)=X+Y\)
\(n(B)=Y+Z\)
\(n(A∩B)=Y\)
\(n(A∪B)=X+Y+Z\)
であるので、集合Aの要素と集合Bの要素を足すだけだと、Yの部分\(A∩B\)が重複してしまうのでその分は省きましょうという式です。
よくある例題
集合についての例題をいくつか紹介していきます。
例題 (要素を書き出す)
nは整数として、集合\(A={2n∣1≤n≤5}\)を要素を書き並べて表せ。
解答
nに1から5の整数を代入していったものが集合Aの要素になるので、
A={2,4,6,8,10}
となります
例題 (正誤問題)
集合A={1,2,3,5,8},B={2n-1∣1≤n≤3},C={2,3,5,7}, 空集合を\(Φ\)、nは整数とする。次の①~⑤から正しいものをすべて選べ。
①\(B⊂A\)②\(C⊂A\)③\(A⊂A\)④\(A=B\)⑤\(Φ⊂B\)
解答
①Bの要素はすべてAに属しており、BはAの部分集合であるので\(B⊂A\)は正しい。
②Cの要素の中で7はAに属さず、CはAの部分集合ではないので\(C⊂A\)は誤り。
③Aの要素はすべてAに属しており、AはA自身の部分集合であるので\(A⊂A\)は正しい。
④AとBの要素は一致していないので\(A=B\)は誤り。
⑤空集合はすべての集合の部分集合であるので、\(Φ⊂B\)は正しい。
よって、正しいのは①、③、⑤
例題 (集合を求める)
U={1,2,3,5,6,7,8}を全体集合とする。Uの部分集合A={2,4,6,8},B={2,3,5,6}について、次の集合を求めよ。
①\(\bar{(A∪B)}\)②\(\bar{A}∩B\)
解答
集合U、A、Bは下の図のように表すことができる。
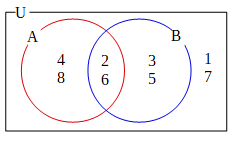
よって、
①\(\bar{(A∪B)}={1,7}\)
②\(\bar{A}∩B={3,5}\)
集合は基礎
この集合という単元では新しくいろいろな記号が出てきます。ここで出てくる記号や法則、考え方はここから先の数学で出てきます。先の内容の基礎となる部分なので、しっかりと意味などを理解して身に付けておきたいですね。