数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。今回は高校2年生の数学の中でも図形と方程式について書いていきたいと思います。高校1年生のときも図形は出てきましたが「図形と方程式」では方程式とxy平面上のグラフを行き来します。基本的なところからしっかりとおさえていきましょう。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
直線と円
点と直線
2点間の距離
2つの点A\((x_a,y_a)\)とB\((x_b,y_b)\)の距離は三平方の定理から、
AB=\(\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}\)
直線の方程式
2つの点A\((x_a,y_a)\)とB\((x_b,y_b)\)を通る直線の方程式は、
①\(x_a≠x_b\)のとき
傾きが\(\frac{(y_b-y_a)}{(x_b-x_a)}\)でどちらかの点を通る直線を求めればいいので、
\(y-y_a=\frac{(y_b-y_a)}{(x_b-x_a)}(x-x_a)\)
②\(x_a=x_b\)のとき
yの値に関係なくxが一定であるので、
\(x=x_a\)
また、2つの直線\(y=mx+n\)、\(y=m’x+n’\)が平行になるときの条件は、
\(m=m’\)
垂直になるなるときの条件は、
\(mm’=-1\)
点と直線の距離
点と直線の距離とは「点と直線の最短距離」のことをいいます。
点から直線に線を引くことを考えたとき、一番線が線が短くなる
のは垂線を引いたときであるので、点と直線の距離とは点から直
線に引いた垂線の長さのことです。
直線\(ax+by+c=0\)と点P\((x_1,y_1)\)の距離dは、
\(d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
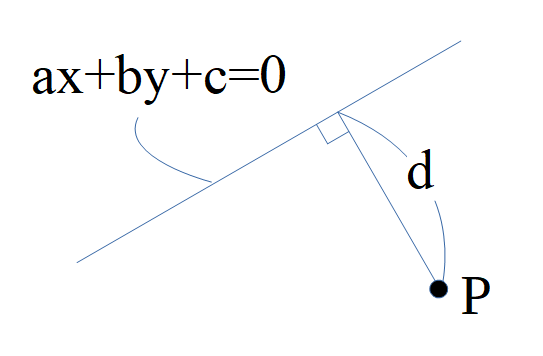
円の方程式
円の方程式
中心\(( p , q )\)、半径rの円の方程式は、
\((x-p)^2+(y-q)^2=r^2\)
と表される。また、円の方程式は一般にl , m , nを定数として、
\(x^2+y^2+lx+my+n=0\)
と表すことができる。
円と直線の共有点
円と直線の共有点を求めるとき、円の方程式と直線の方程式からyまたはxを消去して得られる2次方程式から共有点を求めることができます。しかし、共有点の個数を求める問題など、円と直線の位置関係のみで答えが求まる問題では、点と直線の距離の公式を使うと便利です。
具体的には円の中心と直線の距離が円の半径よりも大きければ交わらず、小さければ2点で交わります。円の中心と直線の距離が円の半径と同じならば直線は円の接線です。
円の接線
円\((x-p)^2+(y-q)^2=r^2\)上の点( a , b )における接線の方程式は、
\((a-p)(x-p)+(b-q)(y-q)=r^2\)
と表すことができます。
円の外にある点から円に引いた接線の方程式を求めるときは、はじめに接点を( a , b )と仮において、( a , b )における接線が条件にある円の外の点を通ると考えて問題を解いていきましょう。
軌跡と領域
軌跡と方程式
軌跡とは、ある条件を満たしながら点が動いたときにできる図形のことをいいます。
問題で与えられた条件から軌跡を求めるときは、次のような手順で求めることができます。
①条件を満たす点Pの座標を( x , y )とおく。
②与えられた条件からx、yの関係式を求め、整理した式が求める軌跡の方程式です。
③求めた軌跡が条件を満たすことを示す。
手順からも分かるように与えられた条件を式におこす手順②が一番難しいところです。また、問題を解くときに手順③を忘れてしまうことがよくありますが、軌跡の問題では必ず必要なので気を付けるようにしましょう。
不等式の表す領域
領域とはある条件を満たす点の集合のことをいいます。これだけだと分かりにくいと思うので、まずは軌跡と領域の違いを考えてみましょう。軌跡になるような条件Aと領域になるような条件Bは次のようなものがあります。
条件A：原点Oからの距離が1である点P( x , y )
条件B：原点Oからの距離が1以下である点P( x , y )
条件Aを満たすのは原点を中心とした半径1の円周になります。それに対して、条件Bを満たすのは原点を中心とした半径1の円の内部になります。このように平面的な広がりをもつときは軌跡とはいわず、領域といいます。つまり問題の条件が不等式で表されるようなときは領域にということです。また、領域とそうでない部分の境目を境界といいます。
よくある例題
図形と方程式についての例題をいくつか紹介していきます。
例題 (直線の方程式)
点( 7 , 3 )を通り、直線\(3x + y – 3 = 0\)に垂直な直線の方程式を求めよ。
解答
直線\(3x + y – 3 = 0\)の傾きは－3であるので、求める直線の傾きは、
\(m⋅(-3)=-1\)
から\(m=\frac{1}{3}\)
よって、求める直線は\(y-3=\frac{1}{3}(x-7)\)から
\(y=\frac{1}{3}x+\frac{2}{3}\)
例題 (点と直線の距離)
円\(x^2+y^2=5\)と直線\(y=2x+a\)が接するときのaの値を求めよ。ただし、aは実数とする。
解答
円\(x^2+y^2=5\)の中心( 0 , 0 )と直線\(y=2x+a\)の距離dは、
\(d=\frac{|2⋅0+(-1)⋅0+a|}{\sqrt{2^2+(-1)^2}}=\frac{|a|}{\sqrt{5}}\)
円の半径とdが一致するとき、円と直線は接するので、\(d=\sqrt{5}\)となればいいので、
\(\frac{|a|}{\sqrt{5}}=\sqrt{5}\)
よって、
\(a=±5\)
例題 (円の方程式)
2つの点( -2 , -3 )、( 6 , 5 )を直径の両端とする円の方程式を求めよ。
解答
直径の中点が円の中心であるので、
\((\frac{-2+6}{2},\frac{-3+5}{2})\)
よって求める円の中心は\(( 2 , 1 )\)
また、2つの点の距離が直径であるので半径rは、
\(r=\frac{1}{2}\sqrt{(-2-6)^2+(-3-5)^2)}\)
\(=\sqrt{\frac{1}{2}⋅(64+64)}=\sqrt{32}\)
よって求める円の方程式は、
\((x-2)^2+(y-1)^2=32\)
例題 (領域)
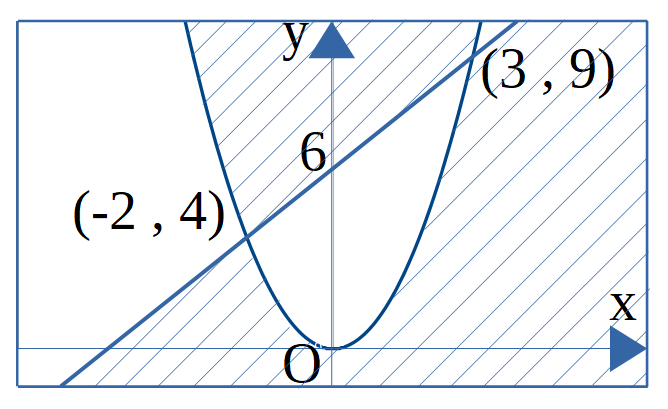
不等式\((x-y+6)(y-x^2)<0\)の表す領域を図示せよ。
解答
不等式\((x-y+6)(y-x^2)<0\)の表す領域は、
\(\begin{eqnarray} \begin{cases} x – y +6 < 0 & \\ y – x^2 > 0 & \end{cases} \end{eqnarray}\)
\(\begin{eqnarray} \begin{cases} x – y +6 > 0 & \\ y – x^2 < 0 & \end{cases} \end{eqnarray}\)
の2つの領域を合わせたもので下の図の斜線部分である。
ただし、境界線を含まない。
図形と方程式攻略法
図形と方程式では、図形から式、式から図形という問題が主に出てきます。それに加えて、文章で表されている条件文を式や図形で表すことが必要になってきます。この単元が苦手だと感じる人は、条件文を式や図形で表すのが苦手な人が多いです。苦手意識のある人はまずどのような図形で表されるかイメージできるようにしましょう。その次にイメージした図形になるような条件を式で考えていくようにしていきましょう。なので、苦手な人の練習の仕方としてはまず、問題文から図形をイメージし、そのイメージになるための条件を調べて問題を解いていきましょう。慣れてきたら条件も自分で考えるようにしましょう。
