こんにちは、株式会社あすなろスタッフのカワイです。
このページでは、直線と角の関係について解説していきます。
角は角でも、それらの位置関係で名前が変わったり、直線が複数並んでいると、特別な性質を持ったりします。結構面白い特徴があったりするので、良かったらゆっくり見ていってください!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
わからない…を“わかる!”に変える家庭教師
「勉強がわからない」そんな悩みは、あすなろ関西の家庭教師が解決!一人ひとりに合った勉強方法で、小学生から高校受験までサポート!
たった15分の勉強で、これまでの3倍の効果を実感!そんな効率的な学びを、無料体験で試してみませんか?

=もくじ=
直線と角の性質
角は直線と直線が交わることによってできます。なので、直線の重なり方や位置関係によって、それぞれの角を特徴づけられることがあります。
対頂角
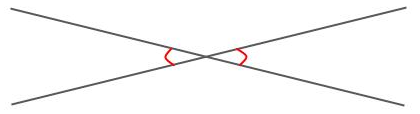
2つの直線によって角がつくられるとき、向かい合っている角のことを対頂角といいます。
同じ直線で線を挟んで出来ているので、向かい合う角の角度は等しくなります。
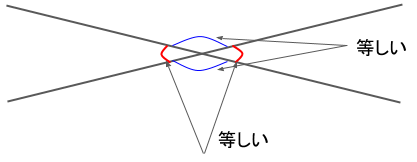
また、2つの直線を任意で重なるように引いたとき、対頂角は2つできます。
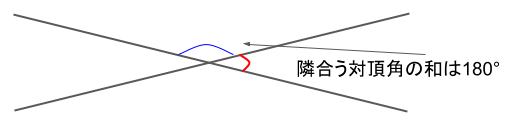
図を見ると分かりやすいと思いますが、その対頂角のそれぞれの角度を足し合わせると180°になります。
2つの対頂角がすべて等しい時(90°の時)、調べずとも明らかですが、その直線は垂直に交わります。
同位角・錯角
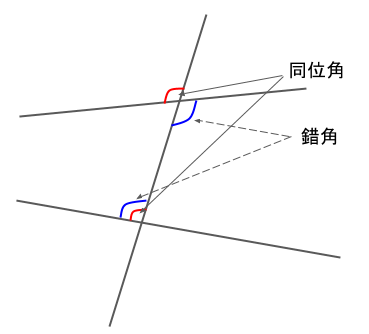
2本の直線とそれを横切るように引かれた1本の直線があるとき、赤い曲線で示した角の位置関係にある角を同位角といいます。
また、青い曲線で示した角の位置関係にある角を錯角といいます。
どっちかわからなくなる人がいるかもしれませんが、
同位角は同じ向きに出来ていて、錯角は対頂角のように向かい合ったような向きの組み合わせになります。


平行線と同位角・錯角
今度は2本の直線を平行に並べて、もう1本の直線がそれらを貫くようにあったとします。
すると、以下の図の通りになります。
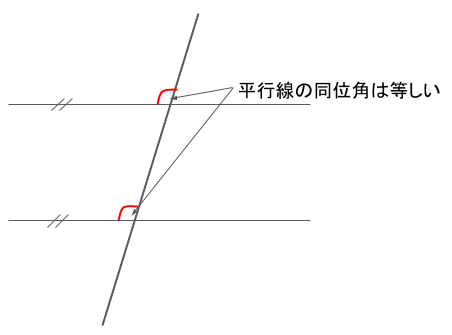
同位角を赤い曲線で示しましたが、平行線の同位角は等しくなります。
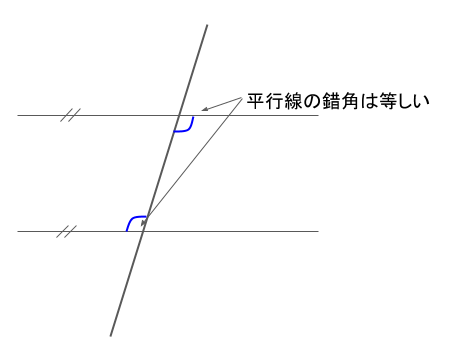
また、錯角を青い曲線で示しました。こちらも同位角と同様に等しくなります。
平行線の性質・条件
直線が平行であるとき、必ず同位角、錯角のそれぞれが等しくなり
逆に、同位角、錯角がそれぞれ等しい時、2直線は平行となります。
これらは相互関係にあり、どちらかが成り立つとき、もう片方も成り立ちます!
【応用】 平行線での対頂角・同位角・錯角の関係
平行線でできた角のうち、これらの関係について考えてみます。
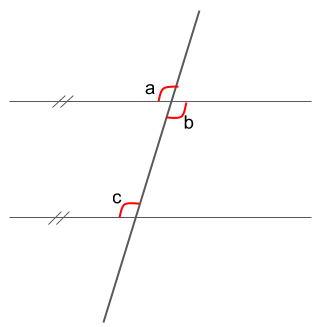
角aは角bと対頂角の関係にあります。一方で、角aと角cは同位角であり、角bと角cは錯角です。対頂角はいかなる場合も等しく、同位角・錯角は平行線でできた角のときそれぞれ等しくなります。
従って、角a=角b、かつ角b=角c、角c=角a
となるので、これらの角は
角a=角b=角c
という関係にあることが分かります。
角a~角cのいずれか1つの角度さえ決定すれば、残り2つの角度も同時に決まるということで、面白く便利な性質です。


まとめ
- 対頂角は等しい。
- 同位角・錯角は、平行線にあるとき、それぞれ等しくなる。
- 2本の直線は、同位角・錯角が等しい時、平行である。
やってみよう!
次の角に合う角を選ぼう
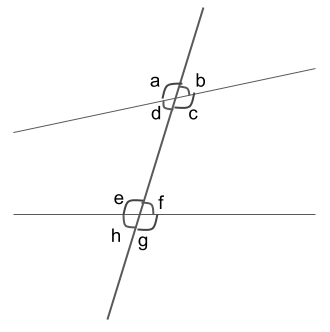
- 角hの対頂角
- 角fの錯角
- 角aの同位角
- 角gと角度が等しい角
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
”やる気”と”自信”を育てる、あすなろ関西の学習サポート
どんな単元もコツをつかめば驚くほどスムーズに理解できるようになります! だからこそ、一人で悩み続ける必要はありません。
あすなろ関西は、「やる気づくり」や「できる喜び」を一番に考え、得意な教科から指導することで自信を持ってもらうことを重視しています。
まずはその第一歩として、自宅でもオンラインでも受けられる無料体験授業を、ぜひお気軽にお試しください!