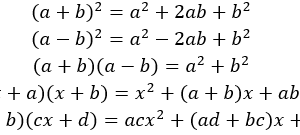高校数学が苦手な方は多いのではないでしょうか?
中学校では数学が得意だったのに、高校生になったら授業にもついていけなくなってしまった…という声もよく聞きます。
つまり、それくらい高校数学はつまづきやすいということです。
そこで、今回は特に苦手意識を持ちやすい「三角比」を徹底解説していきたいと思います。
三角比は数学だけでなく、物理にも登場するのでとても大切な単元ですが、新しい概念のため嫌いだと思っている方が本当に多いです。
授業が分からなかった方、理解があいまいで復習したい方、授業の前に予習して周囲と差をつけたい方必見です!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
三角比とは
三角比とは名前の通り三角形の比です。
- sin(サイン)
- cos(コサイン)
- tan(タンジェント)
といった風に表されます。

上の直角三角形(辺の長さがa,b,c,左下の角度がθ)で表すと、
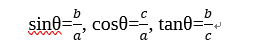
という式で表せます。これがすべての基本になります。絶対に覚えてください!
この単元ではこのサイン、コサイン、タンジェントを使って図形の面積や角度などの値を求めていきます。
では、その際に必要な公式を見ていきましょう!ポイントは、これから紹介する公式はすべて、上記の基本から生まれているという事です。
よく使う大事な公式
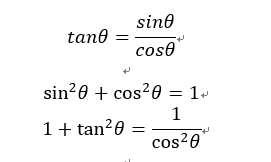
これらの公式も基本中の基本で重要な公式です。計算問題には絶対に必要な知識なので暗記しましょう!
また、公式は計算することで証明できるので、確認していきましょう。
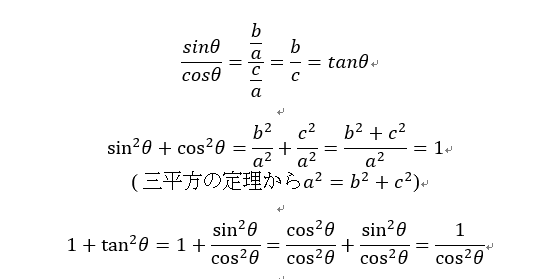
新しい公式が出てきたらその公式の証明を自分で説明できるようにしましょう。そうすることで、公式の暗記率も理解度も向上します。
よくある例題
上の公式を使った例題をいくつか紹介していきます。これは基本問題なので、何も見ずに解けるようにしておきましょう。
例題(\(tanθ=\frac{sinθ}{cosθ}\)を使う)
0° < θ < 180° でtanθ=\(\frac{5}{12}\)の時sinθ、cosθを求めよ。
解答
tanθ=\(\frac{5}{12}\) から、三角形の3辺のうち、2辺は\(5a\)、\(12a\)と表せます。 (sin、cos、tanは比なので\(a\)をかけています)
そうすると三平方の定理から残りの1辺は\(13a\)と表せます。\(((5a)^{2}+(12a)^{2}=169a^{2}\)から)
三角形の3辺が分かったので後はtanθ=sinθ/cosθから
sinθ=\(\frac{5}{13}\), cosθ=\(\frac{12}{13}\)
と求められます。
例題(\(sin^{2}θ+cos^{2} θ=1\)を使う)
0° < θ < 180° でsinθ+cosθ=1/3の時、sinθcosθを求めよ。
解答
\(sin{\theta}cos{\theta}\)を求めるためにはまず\(sin\theta+cos\theta\) を2乗します。そうすると
\(sin^{2}{\theta}+2sin{\theta}cos{\theta}+cos^{2}{\theta}=\frac{1}{9}\)
となります。 \(sin^{2}θ+cos^{2} θ=1\)なので
\(1+2sin{\theta}cos{\theta}=\frac{1}{9}\)
\(sin{\theta}cos{\theta}=-\frac{4}{9}\)
と求められます。
例題(\(1+tan^{2}\theta=\frac{1}{cos^{2}\theta}\)を使う)
0° < θ < 90° で\(cos\theta=\frac{4}{5}\) の時、\(tan\theta\) 求めよ。
解答
\(1+tan^{2}\theta=\frac{1}{cos^{2}\theta}\)を使うだけで求めることができます。
\(tan^{2}\theta=\frac{1}{cos^{2}\theta}-1=\frac{1}{\frac{4^{2}}{5^{2}}}-1=\frac{25}{16}-1=\frac{9}{16}\)
0° < θ < 90°の時は\(tan\theta>0\)であるので
\(tan\theta=\frac{3}{4}\)
苦手克服法
よくある悩み
- 「公式は暗記したのに、問題が解けない…」
- 「どの公式を使って問題を解けばよいか分からない…」
- 「公式は知ってるけど、そもそもsin、cos、tanってどこ」
三角比が苦手な人でよくあるのが、公式は暗記したけど問題を前にするとどの公式を使ったらいいのかわからない、という人です。そもそもsin、cos、tanがどこか全然わからない、という人も多いです。
これらの原因は下記だと考えられます。
- 公式の証明ができない(公式の成り立ちが理解できていない)
- 演習量が足りない
- 練習問題を自力で解かず、解答を写している
数学は公式をただ暗記しただけでは点数が取れない教科です。
数学は知っているから解けるのではなく、「理解して解いたことがあるから」解けるのです。
つまり、理解していない公式をただ暗記している人や、覚えた公式を使って練習問題を解いたことが無い人は、努力しても結果として報われないことが多いのです。
そんなあなたは
下記の順番で勉強してみてください。
- 公式を暗記する
- 公式を証明できるようにして理解する
- 練習問題の解法を暗記・理解する
- 練習問題を自力で解く
1と2は定着すれば何度も繰り返す必要はありませんが、3と4は新しい問題形式が出るたびに繰り返しましょう。
これが勉強を結果につなげる方法であり、三角比を完全に理解し得点源とするために必要な努力です。
4まで至らず、本当に惜しい人もいます。テストをいざ受けたときに「知っている問題だけど、なぜか解けない」という状況です。これは圧倒的に演習量が足りていません。多くの問題の対策をすることに夢中になるのではなく、確実に1問解けるようにしてみましょう。具体的には、解答を見て理解できたと思った問題でも、「解答を見ずに自力で」解けるか必ず確認していきましょう。
三角比攻略法
やるべきことは公式の意味をしっかり理解して、問題がきたらどの公式を使えばいいかすぐにわかるようにしていくことです。
公式の理解に有効なのが公式の証明です。授業で公式を習う時にどのようにしてその公式が成り立つのかを一度は説明されると思います。公式の証明をしっかりと自分で説明できるようになれば、公式について理解がちゃんとできているでしょう。ここでも、理解することが大切なので、公式の証明を暗記してもあまり意味はありません。公式を自分の言葉で説明できるようになりましょう。