数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。今回は高校2年生の数学の中でもベクトルについて書いていきたいと思います。ベクトルはここで初めて出てくる内容ですが、理系なら大学入試で必ず出てくる内容です。さらに物理などの他の科目でも必要になってくるので、内容はしっかりと理解しましょう。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
平面上のベクトル
まずベクトルとは大きさと向きをもつもので、矢印で表されることが多いです。大きさと向きの2つが同じなら等しいベクトルとみなし、位置には依存しません。
ベクトルの基本
始点\(S\)から終点\(E\)までのベクトルは、\(\vec{SE}\)と表します。例として、下の図で \(A\)から\(B\)へのベクトルは \(\vec{AB}\) と表し、\(B\)から\(C\)へのベクトルは \(\vec{BC}\) 、 \(A\)から\(C\)へのベクトルは \(\vec{AC}\) と表します。 また、ベクトルでは\(A\)から\(C\)を直線でつないだ \(\vec{AC}\) と\(A\)から\(B\)、\(B\)から\(C\)と順にたどる \(\vec{AB}+\vec{BC}\) 、つまり始点と終点が同じならば同じベクトルであるということです。
\(\vec{AC}=\vec{AB}+\vec{BC}\)
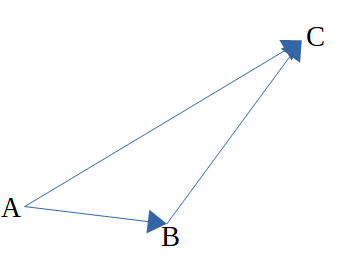
また、向きが逆のベクトルはマイナスをつけて表すことができ、始点と終点を入れ替えた形で表すことができます。\(A\)から\(B\)までのベクトル\(\vec{AB}\)の逆ベクトルは
\(-\vec{AB}=\vec{BA}\)
といったように２パターンの表し方があります。
ベクトルの演算
ベクトルの加法、減法、実数倍については文字式と同じように計算できます。そのため、\(k,l\)を実数として、以下のような式が成り立ちます。
\(
\vec{a}+\vec{b}=\vec{b}+\vec{a} \\
(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c}) \\
\vec{a}+(-\vec{a})=\vec{0} \\
\vec{a}+\vec{0}=\vec{0}+\vec{a}=\vec{a} \\
k(l\vec{a})=(kl)\vec{a} \\
(k+l)\vec{a}=k\vec{a}+l\vec{a} \\
k(\vec{a}+\vec{b})= k\vec{a}+k\vec{b}
\)
また、ベクトルは成分で表すことができるので\(\vec{a}=(a_1 , a_2) , \vec{b}=(b_1 , b_2)\)として成分で計算することができます。
\(
(a_1 , a_2) + (b_1 , b_2) = (a_1 + b_1 , a_2 + b_2) \\
(a_1 , a_2) – (b_1 , b_2) = (a_1 – b_1 , a_2 – b_2) \\
k(a_1 , a_2) = (ka_1, ka_2 ) \\
\)
ベクトルの内積
この「ベクトル」という単元で、ベクトルの内積は避けて通ることはできません。この内積を使うとベクトルとベクトルの間の角度を求めたり、三角形の面積を求めたりすることができます。計算自体は難しくないので定義の式からしっかりと覚えましょう。
内積の定義
\(
\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| cos\theta
\)
この式の\(cos\theta\)の角度\(\theta (0^\circ< \theta <180^\circ)\)は２つのベクトルの間の角です。この内積では気を付けなければならないことが２つあります。
・間の「・」を省略してはいけない。
・内積を計算するとベクトル量でなく、スカラー量になる。
2つ目のベクトル量ではなく、スカラー量であるというのは、内積は大きさと向きをもつベクトル量ではなく、向きをもたないスカラー量になるということです。また、ベクトルの内積は\( \vec{a}=(a_1 , a_2) , \vec{b}=(b_1 , b_2) \)と成分表示した各成分を使って計算することもできます。
\(
\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2
\)
ベクトルの内積は文字の積の計算のように交換法則などの法則が成り立ちます。
\(
\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \\
\vec{a} \cdot (\vec{b}+\vec{c}) = \vec{a} \cdot \vec{b} +
\vec{a} \cdot \vec{c} \\
(\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \\
(k\vec{a}) \cdot \vec{b} = \vec{a} \cdot (k\vec{b}) = k(\vec{a} \cdot \vec{b}) \\
\vec{a} \cdot \vec{a} = |\vec{a}|^2 \\
\)
また、この内積を利用して2つのベクトルの間の角を求めることができます。ベクトルの定義式を式変形すると以下のような式が成り立ちます。
\(
\displaystyle cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} = \frac{a_1 b_1 + a_2 b_2}{\sqrt{a_1^2 + a_2^2}\sqrt{b_1^2 + b_2^2 }}
\)
この式から、2つのベクトルの成分または、ベクトルの大きさと内積がわかれば2つのベクトルの間の角度を求めることができます。この\(cos\theta\)がゼロになると2つのベクトルが垂直です。ベクトルの大きさはゼロより大きいので、内積がゼロになるのが、2つのベクトルが垂直になる条件です。
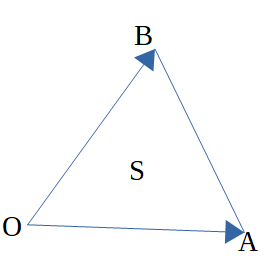
また、下のような△OABで\(\vec{OA} = \vec{a} , \vec{OB} = \vec{b} \)とすると、 △OABの面積Sは、
\(
\displaystyle S = \frac{1}{2} \sqrt{|\vec{a}|^2|\vec{b}|^2 – (\vec{a} \cdot \vec{b})^2}
\)
と表すことができます。
空間ベクトル
空間のベクトルでは、平面の時と比べてパラメータが1つ増えますが、平面上のベクトルの公式等がそのまま使えます。
空間のベクトルでの公式
空間のベクトルでも同じように成立する公式を紹介していきます。まず、２点\(A(x_1 , y_1 , z_1) , B(x_2 , y_2 , z_2)\) 間の距離は、
\(
|\vec{AB}| = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}
\)
と表すことができます。ベクトルの基本的な演算は全く同じ式が成り立ちます。
\(
\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \\
(\vec{a} + \vec{b})+\vec{c} = \vec{a} + (\vec{b} +
\vec{c}) \\
\vec{a} + (-\vec{a}) = \vec{0} \\
\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a} \\
k(l\vec{a}) = (kl)\vec{a} \\
(k+l)\vec{a} = k\vec{a} + l\vec{a} \\
k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b} \\
\)
また、ベクトルを\(\vec{a}=(a_1 , a_2 , a_3) , \vec{b}=(b_1 , b_2 , b_3) \)といったように成分表示すると、
\(
(a_1 , a_2 , a_3) + (b_1 , b_2 , b_3) = (a_1 + b_1 , a_2 + b_2 , a_3 + b_3) \\
(a_1 , a_2 , a_3) – (b_1 , b_2 , b_3) = (a_1 – b_1 , a_2 – b_2 , a_3 – b_3) \\
k(a_1 , a_2 , a_3) = (ka_1 , ka_2 , ka_3) \\
\)
内積はの定義式はまったく同じ式ですが成分表示して計算するとz成分が追加された形になります。
\(
\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| cos\theta = a_1 b_1 + a_2 b_2 + a_3 b_3 \\
\)
2つのベクトルの間の角度を求める公式も増えたz成分の項が加わった式になっています。
\(
\displaystyle cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} = \frac{a_1 b_1 + a_2 b_2 + a_3 b_3}{\sqrt{a_1^2 + a_2^2 + a_3^2}\sqrt{b_1^2 + b_2^2 + b_3^2 }}
\)
空間の中での方程式
空間でのベクトルを使った方程式は直線と平面の方程式がよく出てきます。点\(A(x_1 , y_1 , z_1)\)を通り、ベクトル\(\vec{u}=(l , m , n)\)に平行な直線の方程式は、
\(
\displaystyle \frac{x – x_1}{l} = \frac{y-y_1}{m} = \frac{z – z_1}{n}
\)
と表すことができます。
また、点\(A(x_1 , y_1 , z_1)\)を通り、ベクトル\(\vec{n}=(a , b , c)\)に垂直な面\(α\)はただひとつだけに決まり、この平面の方程式は、
\(
a(x-x_1)+b(y-y_1)+c(z-z_1)=0 \\
\)
と表すことができます。
よくある例題
ベクトルについての例題をいくつか紹介していきます。
例題 (ベクトルの成分)
\( \vec{a} = (-2 , 3) , \vec{b} = (4 , -1) \) のとき、\( \vec{p} = (10 , 0) \) を \( \vec{p} = s \vec{a} + t \vec{b} \) の形で表せ。
解答
\( \vec{p} = s \vec{a} + t \vec{b} \) を成分で表すと、
\( (10 , 0) = s (-2 , 3)+ t (4 , -1) =(-2s+4t , 3s-t ) \)
よって、
\begin{eqnarray}
\left\{
\begin{array}{l}
10 = -2s + 4t & \\
0 = 3s – t &
\end{array}\right.
\end{eqnarray}
\(
s=1 , t=3
\)
よって、
\(
\vec{p} = \vec{a} + 3 \vec{b}
\)
例題 (内積)
次の内積を求めよ。
①\( |\vec{a}|=2 , |\vec{b}|= 5 \)で２つのベクトルのなす角が\(60^\circ\)のときの内積
②\( \vec{a} = (1 , 7) , \vec{b} = (3 , -4) \)のときの内積
解答
①、②ともに内積の定義に従って計算します。
①
\(
\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|cos\theta = 2 \times 5 \times \frac{1}{2} = 5
\)
②
\(
\vec{a} \cdot \vec{b} = 1 \times 3 + 7 \times (-4) = -25
\)
例題 (ベクトルのなす角)
次の2つのベクトルのなす角を求めよ。
①\( \vec{a} =(1 , 7 , 2) , \vec{b} = (1 , 4 , -1) \)
② \( \vec{a} =(7 , 1 , 2) , \vec{b} = (1 , 1 , -4) \)
解答
\( \displaystyle cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} = \frac{a_1 b_1 + a_2 b_2 + a_3 b_3}{\sqrt{a_1^2 + a_2^2 + a_3^2}\sqrt{b_1^2 + b_2^2 + b_3^2 }}\)を使って計算すると、
①
\(
\displaystyle cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} = \frac{1\times 1 + 7 \times 1 + 2 \times (-1)}{\sqrt{1^2 + 7^2 + 2^2}\sqrt{1^2 + 4^2 + (-1)^2 }} = \frac{27}{\sqrt{54} \sqrt{18}} = \frac{\sqrt3}{2}
\)
\(0^\circ < \theta < 180^\circ\) なので、\( \theta = 30^\circ \)
②
\(
\displaystyle cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} = \frac{7\times 1 + 1 \times 1 + 2 \times (-4)}{\sqrt{7^2 + 1^2 + 2^2}\sqrt{1^2 + 1^2 + (-4)^2 }} = 0
\)
\(
0^\circ < \theta < 180^\circ\)なので、\( \theta = 90^\circ \)
例題 (平面の方程式)
点\( A(-5 , 2 , 1) \)を通り、ベクトル\( \vec{n} = (1 , -1 , 1) \)に垂直な平面の方程式を求めよ。
解答
点\( A(x_1 , y_1 , z_1) \)を通り、ベクトル\( \vec{n} = (a , b , c) \)に垂直な平面\(\alpha\)の方程式は、
\(
a(x-x_1)+b(y-y_1)+c(z-z_1)=0 \\
\)
と表されるので求める方程式は、
\(
1(x+5)+(-1)(y-2)+1(z-1)=0 \\
\)
よって、整理すると、
\(
x – y + z + 6 = 0
\)
ベクトル攻略法
高校生の数学で今まで文字や式について、学んできたのに対してこの「ベクトル」という単元の内容な大きさに「向き」が加わるという物理よりの内容になっています。同じ大きさでも方向が違ったり、数字だけ見るとわからなかったが計算してみたら同じものだった、など今までの感覚で取り組むと苦戦するかもしれません。ベクトルの問題を解くときは問題文の条件を式で表すことが一番大切です。ベクトルの平行や垂直の条件や平面や直線の方程式の表し方などパターンがいくつかあるので、代表的なものは覚えるようにしましょう。
