こんにちは、あすなろスタッフのカワイです!
今回は多項式の中の項を少なく、簡単にしたり、多項式と数字の乗法について勉強していきましょう!1年生の時に学習した交換法則や分配法則を使って計算をしていくという所は同じので、構えなくても大丈夫です!
読んでいて”よく分からないな…”と思ってしまった方のために、交換法則・分配法則についての解説も後半に少し載せているので、良かったら最後まで読んでみてくださいね!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
同類項をまとめてみよう!
例1 \(3a+4b-2a+b\)
数字と\(a\)、数字と\(b\)という項が複数あるのに、別々になっているので、スマートではありませんね。これを短くすることが出来ます。
同じ要素で構成されている項は計算により一つの項にまとめてしまうことが出来てしまうのです。
どのように計算するかというと…下を見ていきましょう。

まず、式中に同じ文字で構成された項があるかどうかを確認します。
今回の場合は\(3a\)と\(-2a\),\(4b\)と\(b\)がそれぞれ文字の部分が同じになっていますね!
このような文字の部分が同じ項(次数も同じ)を同類項といいます。
同類項が隣になるように(交換法則を用いて)式を変換すると、①のようになります。ここから同類項で計算をすると②のようになります。これより短くすることは可能でしょうか?
それは、できません。ここまで短くすることができればOKです。元の式よりかなりスッキリしたと思いませんか?!
例2 \(5a^{2}+3a-2a^{2}-a\)
今度の多項式はすべて同じ文字が使われていますね!全部同類項だから単項式に書き換えられるのでは?!
と思うかもしれませんが、それは違います!
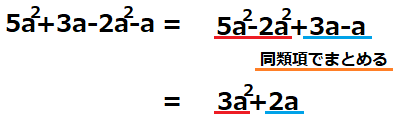
同類項の定義として、次数が同じである必要があります!ですから、この式から同類項で分けると、\(5a^{2}\)と\(-2a^{2}\),\(3aと-a\)となります。
従って、交換法則で同類項を隣合わせにして、計算すると、答えは
\(3a^{2}+2a\)となります!
多項式と数の乗法をしてみよう!
例3 \(5(4a+3b-2)\)
数と多項式の積で表されていて、非常に綺麗な式になっています。さて、これを多項式だけの形で表したいとき、どうしたらいいかというと…下のようになります!
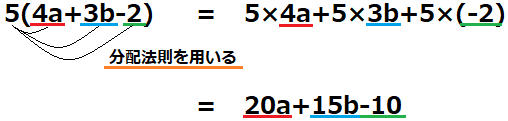
分配法則を使えばいいです!符号だけ注意して分配すると一行目の右辺になります。
これらをそれぞれ計算すると、結果は\(20a+15b-10\)となります!
分配して、個々で計算するだけです!
最後に、同類項の計算と上の計算の二つを組み合わせて、例4を簡単にしていきましょう!
例4 \(4(2a+3b)-2(3a+2b)\)
手順としては、
- 分配法則して計算する
- 同類項をまとめる
- 計算する
という感じで出来ます!解ける人は頑張って解いてみてください!
では解説していきます!
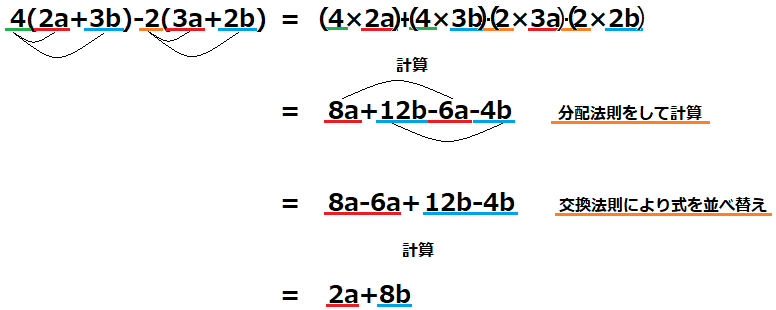
まず、分配法則により、()内のそれぞれの項と外側の数字の乗法をします。
すると、4つのにまとまりました。項に同類項が無ければここでおしまいですが、同類項があるので、交換法則によって同類項を隣にして、計算します。
その結果、\(2a+8b\)の簡潔な多項式になりました!
交換法則・分配法則の復習
今回の内容でつまづいてしまった方は、「交換法則」「分配法則」の理解が十分でないかもしれません。ここで少し復習してみましょう。
- 交換法則とは?
ズバリ、式の中の項を入れ替えても、計算結果が同じという法則です。
この法則は乗法と加法に用いることができます。除法や減法に用いることができません。さて、この意味について例を用いて説明していきます。
例えば、\(3×4\)の答えは\(12\)になりますね。
一方で、\(4×3\)の答えも同様に\(12\)になります。
これは偶然ではなくて、他の乗法についても成り立ちます。これが交換法則です!
足し算については、自分で好きな数の足し算を考えて、それをひっくり返して計算してみてください。情報と同様に、計算結果は同じになります。
- 分配法則とは?
分配法則とは、△×(〇+□)という形になっているときに、〇+□を計算してから△を掛けるのと、△×〇と△×□の足し算が同じになるという法則です。
交換法則と比べると、少々ややこしい部分があるので、図を使って解説していきます。
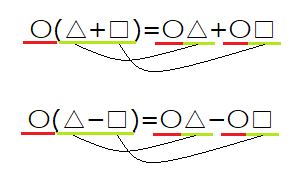
分配法則では、上のような式変形が可能になります。
実際、ここに数字を入れてみると、次のようになります。
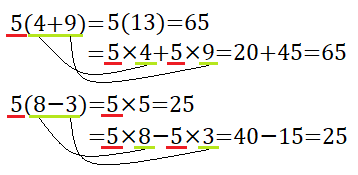
数字だけの式は特に分配法則を用いるメリットがなさそうです。
しかし、文字を含んだ式の場合、分配法則を用いることで、単項式を多項式にすることができます。例えば、
\(5(2a+4)\)という式の場合、分配法則を使わないと、これ以上計算することができません。しかし、分配法則を用いることで、
\(5(2a+4)=10a+20\)とすることができます。
このような形で、数字と文字を含んだ式で分配法則を用いていくことになります。
まとめ
- 文字の部分が同じ項のことを同類項という。(次数も同じでなければならない)
- 同類項は交換法則を用いて並び替えて計算する
- 多項式と数の積は、分配法則を用いて各項を計算する
やってみよう!
問題
次の式を計算してみよう
- \(3a-2b+4a-3b\)
- \(4(2x-3y)+5(x+3y)\)
- \(4(a+b-1)+2(2a-c+2)\)
答え
- \(7a-5b\)
- \(13x+3y\)
- \(8a+4b-2c\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
数学は単元の繋がりが強い教科なので、「わからない!」という単元が出てきたときは、そこに関連する単元を学習し直してしっかりと理解することが、苦手克服の近道です。時には前学年の教科書や参考書を見直すことも効果的ですよ。
家庭教師のあすなろ関西では、学校の教科書を中心とした予習・復習を軸に、独自の「あすなろ式ラクラク定着法」を用いて指導をしています。
もちろん先生と1対1の指導なので、学習の理解度に応じてずっと前の単元に戻ることも、先取りの勉強をすることも可能です!
勉強のやり方にお悩みの方・自分に合った勉強法を見つけたい方は、無料の体験授業もやっているので、ぜひお気軽にお試しくださいね!