こんにちは。あすなろスタッフのカワイです。
前回は、負の数を含んだ加法をお話ししました。加法とは足し算のことでしたね。小学校の算数と異なり、数直線からアプローチしていきましたが、分かっていただけましたか?加法のやり方について知りたい方は、前回の記事を読んでみてくださいね!
前回の記事はこちら!:
【中1数学】負の数の足し算のやり方が分からない人必見! 数直線を使った簡単な計算方法
今回は、「負の数の引き算」について、また数直線を利用して解説していきます。引き算も足し算と同様の考え方を使うことが出来ます!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
”どうしても負の数の引き算の説明が分からない…”という人のために、考え方だけでなく、計算の解き方も詳しく解説しています。読み進めていってくださいね!
=もくじ=
小学校で習った引き算の考え方
まず、(+5)-(+3)を計算していきましょう。
この答えを?とすると、
(+5)-(+3)=?
両辺に(+3)を足すと、
(+5)=?+(+3)
つまり、
?+(+3)=(+5)
となります。
これを数直線で表すと、
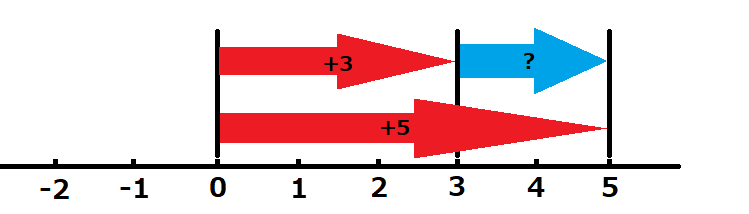
となります。右に3進んだ後にある数を足すことによって、結果は右に5進んだことになるので、?の値は+2となります。
さて、このような問題は小学校のはじめの方で習ったと思うので、数直線を使わなくても暗算でできると思います。ですが、この数直線での考え方が、中学からの計算において重要です!今回の解説で完璧にしましょう。
「減法」と「差」
加法と同様に、引き算のことをこれから「減法」という数学用語を使って説明していきます。また、減法の答えを「差」といいますので、覚えてくださいね!
では、ここから本番です!
例題1 正の数–正の数
(+3)-(+5)を計算してみましょう。前の問題と同様に、答えを?とすると、
?+(+5)=(+3) となります。
これを数直線上で表すとこうなります。
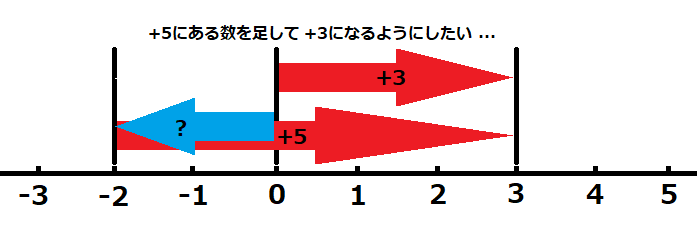
?に進んだ後に、進んだ先から右に5進むと、結果として右に3進むことになるような?が分かればいいわけです。従って、図のように?は左に2進むことになるはずなので、差は-2となります。
このように、正の数同士でも、小さい数から大きい数を引くと、差は負の数になります。
例題2 正の数-負の数
次に、(+2)-(-3)を計算してみましょう。答えを\(?\)とすると、
?+(-3)=(+2)となるので、
これを数直線上で表すとこうなります。
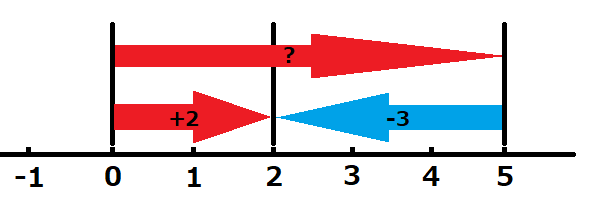
ある数?を足した後に、その先から左に3進んだ結果、右に2進んだこととなるような値が?に入ります。図より、?は右に5進んでいると分かるので、差は+5となります。
式に表すと、(+2)-(-3)=+5となりますね。
ここで、式中の符号をよく見て下さい。(+2)-(-3)=?のように、負の数を引き算する形になっています。
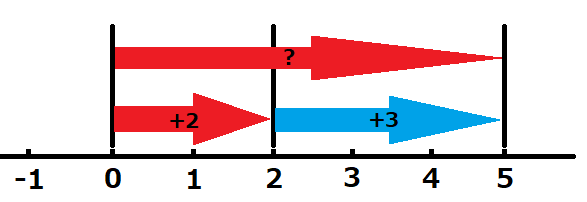
これは、 前の例題の-3をひっくり返したものになりますが、図より(+2)+(+3)=?と書くことができそうですね。
上の図と下の図を見比べてもらうと、?の値が一致していることに気付くでしょうか…? さて、式を比較してみると、
(+2)-(-3)=+5
(+2)+(+3)=+5
となります。これより、(+3)と(-(-3))が同じ数であるという事が分かります!
回りくどい説明になってしまいましたが、-(-数)=数すなわち、「負の数で引く」ことは「正の数を足す」ことと同じになります。少し難しいと思いますが、上の数直線を見比べてみると何となく分かってもらえるのではないかと思います!
同じように「正の数を引く」ことは「負の数を足す」ことと同じになります。
今回の最大のポイントは、繰り返しにはなりますが、
- 「負の数で引く」=「正の数を足す」 例:-(-2)=+2
- 「正の数を引く」=「負の数を足す」 例:-5=+(-5)
ということです!これが理解できれば、負の数の減法を加法に書き換えて解くことができます。
例題3 負の数-負の数
最後に負の数同士の減法をしてみましょう。今回は数直線ではなく、式から計算していきます。
式は(-3)-(-5)=?となりますが、一つ前に説明した符号をひっくり返して計算してみると、(-3)+(+5)=?となります。これは紛れもなく加法になってしまいましたから、計算はすぐできるのではないでしょうか。
よって、差(和)は(+2)となります。もし分からないという方は、数直線を書いてみてください。
どうしても負の数が分からない時は…
上記まで数直線などを使って、負の数を説明してきましたが、「まだ分からない」「しっかり理解できているか不安」という方は見てください!
小学校までの勉強で負の数が出てこなかったので、負の数を含んだ引き算を考えるのはとても難しいですよね。
もし意味を理解することが難しいようであれば、裏ワザ的な解き方で解けるようにしていきましょう。
正の数-正の数の場合
これは、引く数同士の大きさを比べる他ありません。例えば
5-9
であれば、5と9を比べて、大きい方から小さいほうの引き算をします。この場合は9-5=4です。
もし、左の数が右の数より大きい場合はそのまま、
左の数が右の数より小さい場合は、計算結果に(-)を付けます。
符号の付け忘れに注意しましょう!
負の数-正の数の場合
これは比較的簡単です。例えば、
(-6)-(+1)
となるとき、(-(+1))の部分を(-1)としてしまえます。
そうすると(-6-1)となります。これは((-6)+(-1))と同様であるので、足し算をして(-7)となります。
正の数-負の数の場合
これは足し算の形にすることで、簡単に計算することが出来ます。
4-(-6)であるとき、(-(-6))を(+6)に変えることが出来ます。
ということは、これは4+6になるので、小学1年生の算数で解けるレベルまでにできます。
負の数-負の数の場合
正の数-負の数と同様に、簡単な形にすることが出来ます。
例えば、((-3)-(-5))という式があるとき、(-(-5))を(+5)にすることが出来ます。
すると、\((-3)+5\)となります。この式の前後をひっくり返すと、\(5-3\)となります。同様に小学校1年生レベルの式になりました!
まとめ
減法は加法に直すことができます。
- +(+〇)=+〇
- -(+〇)=-〇
- +(-〇)=-〇
- -(-〇)=+〇
減法のしくみについて、分かって頂けましたか?前に示したように、減法は加法に変換することができます。加法と減法が混ざった式も出てきますが、基本的に減法を加法に変換できるので計算可能です!
やってみよう!
問題
次の計算をしましょう
- 5-(-3)
- (-3)-4
- (-7)-(-1)
- (-3)-(-8)
答え
- 8
- -7
- -6
- 5
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。