こんにちは、家庭教師のあすなろスタッフのカワイです!
今回は、円周角の定理とは何か?について解説していこうと思います!
そもそも円周角ってなに?という人もいると思いますが、出てくる用語については詳しく説明しながら進めていくので、よろしければ最後まで読み進めてみてください。
それでは、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。 この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
円周角・弧とは?
円周角とは、文字で表すと、
「円周上に点を3つ置き、3点を2本の線分でつないだ時、その2本の線で出来た角」
のことをいいます。
図形についてを言葉使って説明しても全然伝わらないと思うので、図を示して説明していきますね。

上のような円があったとします。大きさは何でもいいです。
この円の上に点を3つ乗せていくと、
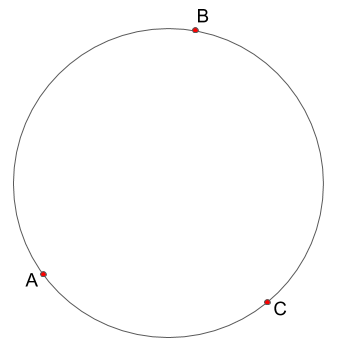
このようになります。点はそれぞれ、点A,点B,点Cとしておきます。
次に、乗せた3つの点の2つの線分でつないでいきます。
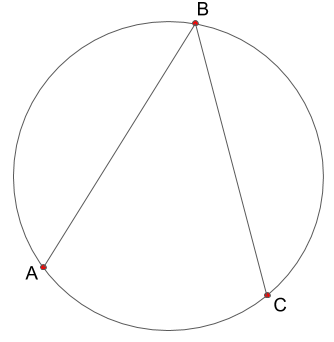
こうすると、線分と線分に挟まれた点Bのところに、角が出来ていることが分かります。
この角を、線分を構成するA,B,Cを用いて∠ABCと表せます。
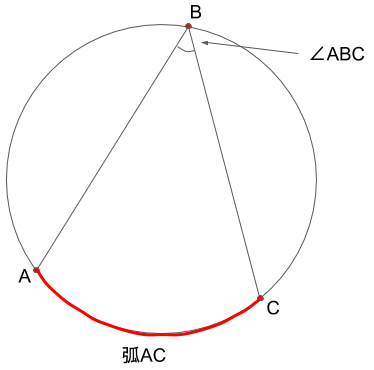
この時、弧ACに対して角が出来ていることから、∠ABCを弧ACに対する円周角と呼びます。
ここで弧とは、ACの間のように、円周上の2点間にある円周上の一部のことをいいます。
これは点Bが特別なわけではなく、つなぎ方によって、
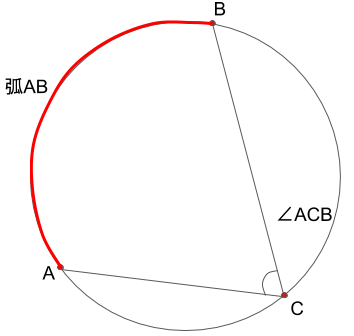
となったり、
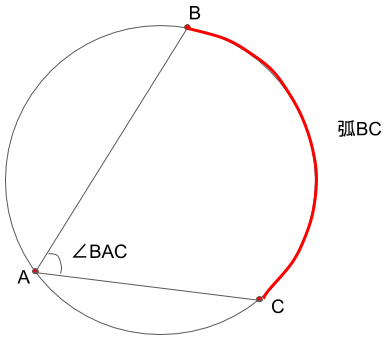
となったりもします。
上については、弧ABに対する円周角∠ACB、
下については、弧BCに対する円周角∠BAC
となります。円周角については、とる点と線分のつなぎ方によって、いろいろ取ることが出来るということです。
同じ弧で出来た円周角の関係
次に、円周角をつくる弧は変えずに点の位置を少しずつ変えてみます。
円周角∠ABC

から、弧ACは変えずに、点Bを少し左寄りに移動させた点B’で円周角をつくると、
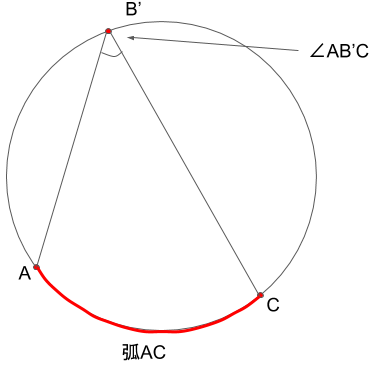
のようになります。また、弧ACは変えずに、点Bから右側に大きく移動させた点B’’で円周角をつくると、
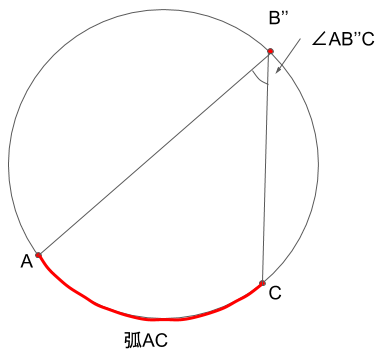
のようになります。これらをまとめて表してみます。
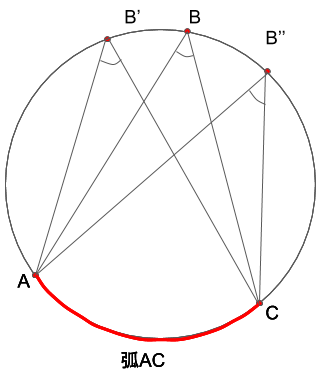
見て分かる通り、角をつくる点は大きく変わりましたが、角度は変わりません。
式で表すと、∠ABC=∠AB’C=∠AB’’Cということです。
弧が同じであれば、同じ円周上(弧の外側)のどの点をとっても円周角は変わらない
ということを覚えてください。
同じ円周上の違う場所の等しい弧による円周角
少し発展して、今度は別の弧だけど同じ円周上の等しい弧を考えてみます。
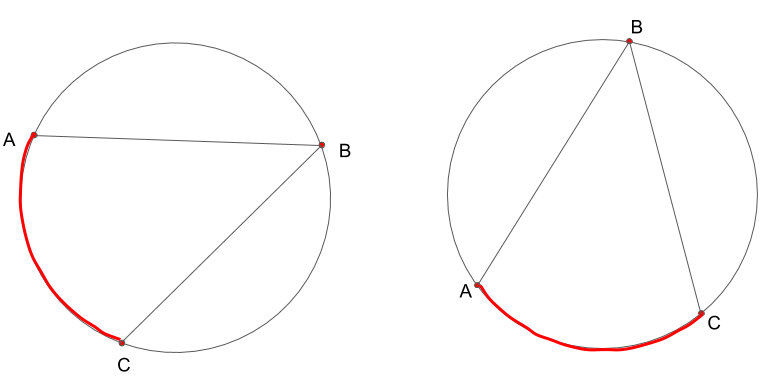
この図で分かると思いますが、同じ円周上の同じ大きさの弧であれば、円自体を回転させればその弧をつくることが出来ます。
ということは、同じ円周上の別の等しい弧からできる円周角の大きさは変わりません!
円周角の大きさは弧の大きさによって完全に決まるということです。
さて、ここまでの事を二つの文でまとめると、
一つの円において、
- 等しい円周角に対する弧は等しい
- 等しい弧に対する円周角は等しい
となります。
中心角とは
次に、中心角について解説していきます。
中心角を一言で言うと、円周角の中心バージョンです。
円周角では、点を円周上に3つ置きましたが、円周上に2つ置いた点と、円の中心をそれぞれ結んだときに出来た角を中心角といいます。
これを図にすると、
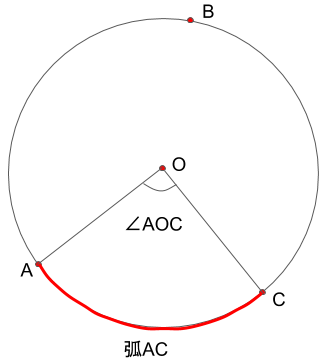
このようになります。中心角も円周角と同じように、弧によって角度は変わります。
また、1つの円において、等しい弧であれば、中心角も等しく、中心角が等しければ、弧が等しくなります。
確認として、他の点による中心角も見てみます。
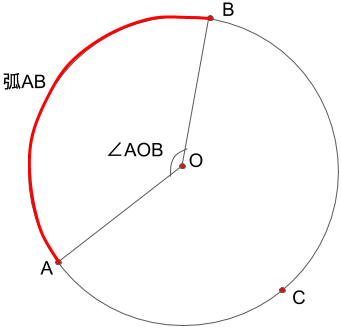
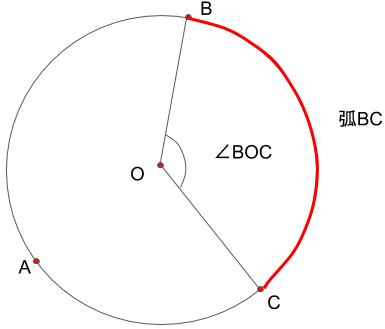
円周角と中心角の関係 ~円周角の定理~
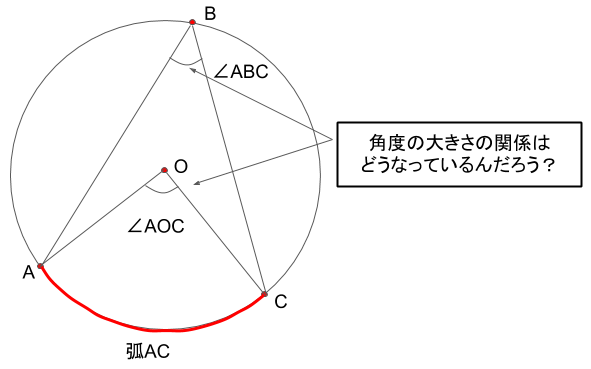
さて、ここで思うのは、
「とある弧に対する円周角と中心角ってどんな関係にあるんだろう?」
ということです。
この大きさについて証明を用いて調べてみましょう。
円周角と中心角の関係とは?
このように、円周上に3点(A,B,C)と円の中心の点Oを考えます。
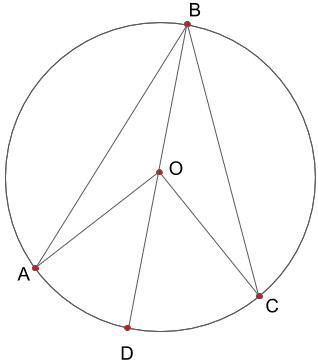
この図の通り、各点を線分で結び、BとOの延長線かつ円周上の点をDとします。
さて、OAとOBはどちらも円Oの半径となるので、OA=OBとなります。
ここで、△ABOは二等辺三角形となるので、
∠OAB=∠OBA
となります。さて、これらを∠aとします。
次に、∠AODという角を見てみると、これは△ABOの外角となっていることが分かるので、
∠AOD=∠OAB+∠OBA=2∠a
となります。
一方、△CBOについても同様に考えることが出来るので、∠OBC=∠bとすると、
∠OBC+∠OCB=∠COD=2∠b
となります。
さて、弧ACに対する円周角と中心角は∠ABCと∠AOCであるから、
∠ABC=∠OBA+∠OBC=∠a+∠b
∠AOC=∠AOD+∠COD=2∠a+2∠b=2(∠a+∠b)=2∠ABC
となります。
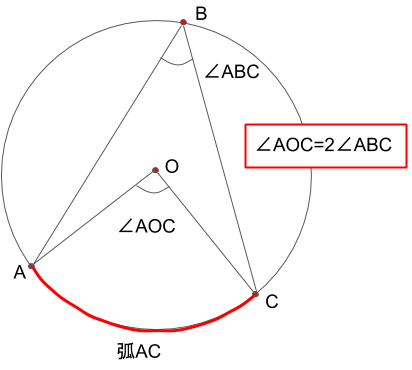
このことから、中心角は円周角の2倍となることが分かりました。
円周角の定理
1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である。
弧が直径の場合
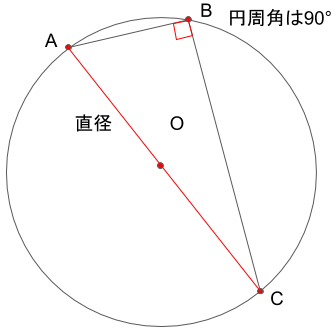
今度は、上で説明した図形のうち、点A,点O,点Cが一直線になる場合を考えてみます。
円周角の定理から明らかなことですが、中心角∠AOCは180°となるので、円周角∠ABCはその半分の90°となります。
さて、ここで点Aと点Cを結んだACは、この円の直径を示すことが分かります。
このことから、
「円の直径に対する円周角は90°となる」
と分かります。(中学でタレスの定理とよばれるものの1つです。この名前を中学では教えません。)
まとめ
円周角と弧
一つの円において、
- 等しい円周角に対する弧は等しい
- 等しい弧に対する円周角は等しい
円周角の定理
- 同じ弧で作られる円周角の大きさは等しく、その弧に対する中心角の半分の大きさとなる。
円周角の定理について知ることで、円の特徴を数学的に捉える方法を新たに手に入れたことになります。
証明で用いられることも多いので、しっかり理解して次の内容に進んでいくようにしましょう。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。