こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、円と相似というテーマについて説明していきます。
相似や円周角の定理を用いて考えていきますが、復習しながら進めていくので、良かったら最後まで読み進めてみて下さいね!
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。 この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
【復習】相似
相似とは、「同じ形」で「長さが違う」図形の関係のことをいいます。
図で表すと、
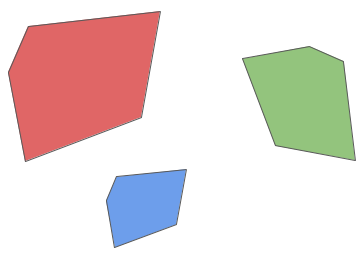
のような関係のことです。図形の位置や向き等は関係なく、
- 対応する角度が等しい
- 対応する辺の長さの比が等しい
を満たしていれば良いです。
ちなみに、対応する角度が等しいだけでなく、辺の長さも等しい場合は、合同であるといいます。
【復習】円周角の定理
円周角の定理とは、円の円周角と弧、中心角の関係について示した定理となります。
その1:同じ弧に対する円周角の大きさは等しい
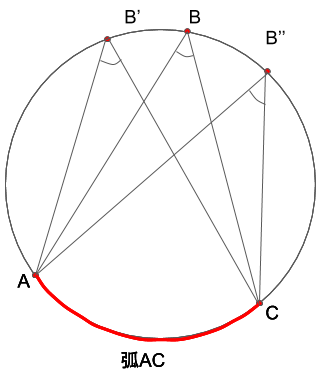
上の図では、弧ACに対する円周角である∠ABC,∠AB’C,∠AB’’Cを示しています。証明は省きますが、この図の様子から分かる通り、同じ弧に対してできる円周角はどれも同じ大きさとなっていることが分かります。
その2:同じ弧に対する円周角の大きさは、中心角の半分である
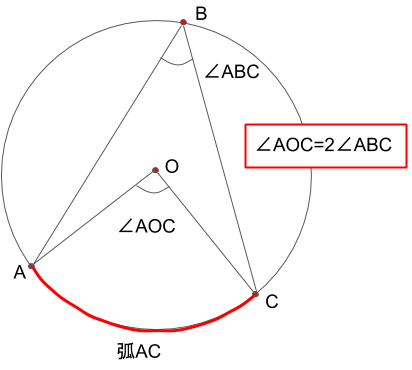
弧に対する円周角の大きさは、中心角の半分となります。なぜこのようになるのかという証明についてはこちらで説明していますので、気になる方は確認してみてください。
円の中の線・図形の関係とは?
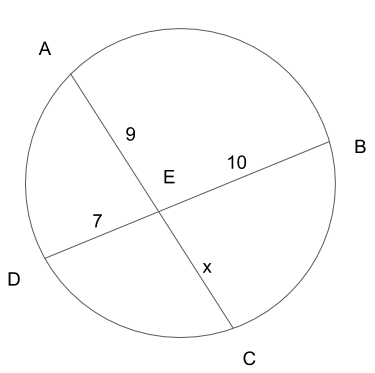
さて、今回はこの図形における\(x\)の長さを求めようと思います。
円の中に直線が2本通っていて、円の真ん中付近で2本の線分が交差しています。そして、線の交点と円周との交点の長さがそれぞれ7,9,10と決まっていて、残り1カ所の長さだけ\(x\)となっており分かりません。この長さを求めたいという問題です。
さて。これをどのように求めていくのかというと、このような円の中の図形問題については、
「円周角の定理」を使って、円の中の線の関係を紐解いていくことで、解くことが出来ます!
数字は一旦置いて、証明によって関係を探していきます。
「円周角の定理を使うって言うけど?円周角なんてないじゃん。」
と思った方、円周角を作ればいいんですよ。
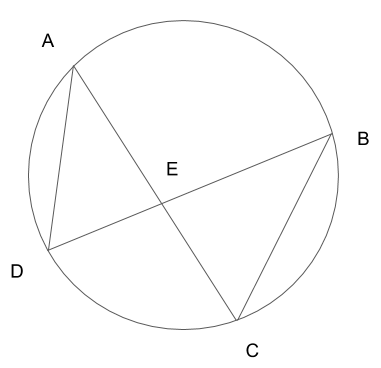
円周との交点の部分に直線をそれぞれ繋いでみました。
直線を引いたことで、角度が4つ出来て、三角形も2つ出来ました。
ところで、この2つの三角形、何か似た形してるな~と思えませんか?
この関係を、円周角の定理を使って関係を暴いていきます!
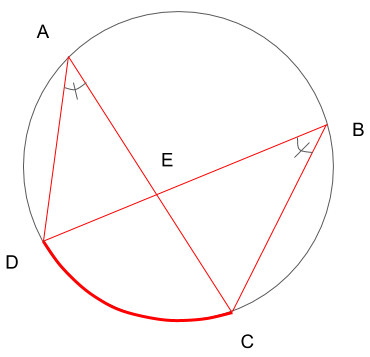
まず、弧DCに着目してみましょう。すると、そこから伸びる直線によって2つの円周角
∠DACと∠CBD
があります。1つの円について、同じ弧に対する円周角の大きさは等しいという円周角の定理より、
∠DAC=∠CBD
であると分かりました。
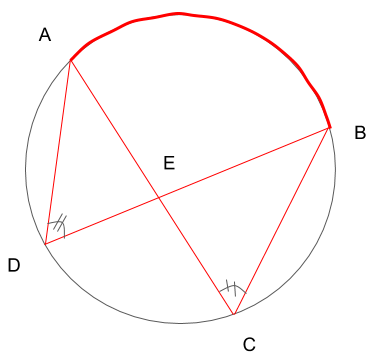
次に、弧ABに着目してみましょう。ここにもまた、弧ABに対する円周角
∠ADBと∠BCA
があります。これらも円周角の定理より、
∠ADB=∠BCA
であると分かりました。
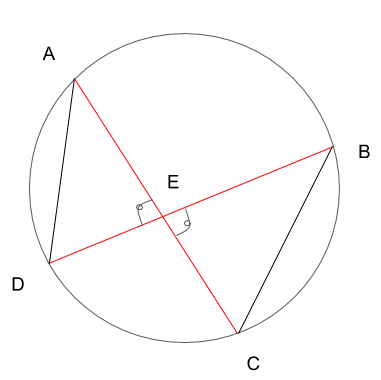
もう1つ、∠AEDと∠BECですが、2本の直線の交点によりなす角なので、対頂角の関係にあります。従って、
∠AED=∠BEC
であると分かります。
さて、これら3つの関係をまとめると、
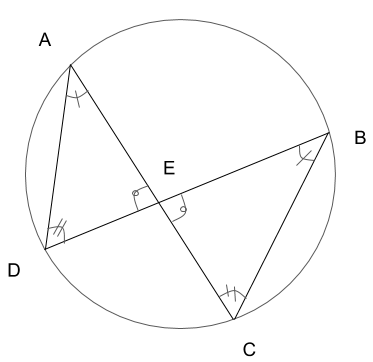
このようになりました。三角形の3組の角がそれぞれ等しくなっています。
三角の相似条件は
- 3組の辺の比がすべて等しい
- 2組の辺とその間の角が等しい
- 2組の角がそれぞれ等しい
のどれかを満たせばいいのですが、
今回の場合、一番下の条件を満たしているので、
2つの三角形は△AEDと△BECは相似の関係となっていることが分かります!
相似ということは、
- 対応する角度が等しい
- 対応する辺の長さの比が等しい
ということなので、各線分について比で表すと、
\(AD:BC=DE:CE=EA:EB\)
となります。
図にすると、
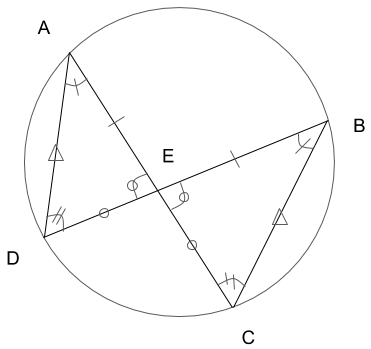
となります。こちらの方が視覚的で分かりやすいかもしれません。(対応する辺を同じ記号で表していますが、辺の長さが等しいわけではありません。)
ここから、元からあった線分についてのみ考えることとすると、
\(DE:CE=EA:EB\)
の式を用いて解いていくことになります。
さて、最初の問題に戻りましょう。
各辺の長さを線分の比の式に当てはめていくと、
\(7:x=9:10\)
となります。これを\(x\)について解くと、
\(x=\frac{70}{9}\)
となります。
従って、問題の線分の長さは\(\frac{70}{9}\)です。
このように、円の中の直線の中に円周角の関係を発見できる場合、比を使って線分の長さを求めることが出来るのです!
今回はACとDBをつないで解いていきましたが、ADとCBをつないで考えても同じように解けます。
もし興味がある方は解いてみて下さい!
円周に交わって出来る線・図形の関係とは?
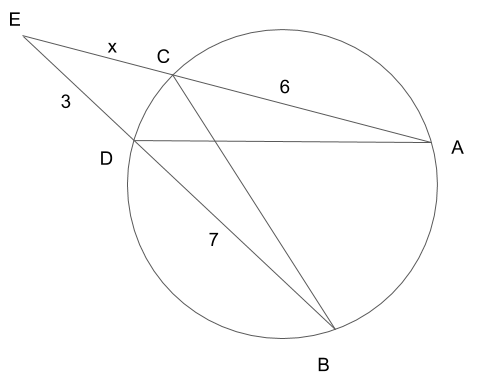
次は、この図形の\(x\)を求めていきます。
考え方は先ほどとそこまで変わらないので、サクッと進めていきましょう。
今回も円周角の定理を用いて、この中の線分の関係を解き明かしていきます!
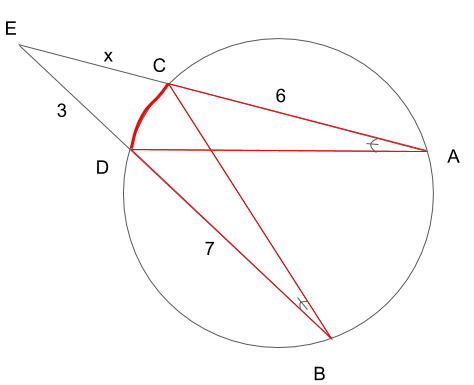
まず、弧CDに円周角∠CADと∠DBCがあることが確認できるので、円周角の定理より、
∠CAD=∠DBC
であると分かります。
これで、この辺の長さの関係を導く準備は終わりました!
今回は円の中にある三角形ではなく、円の外側にある点Eを使った三角形
△ADEと△BCE
に着目すると、
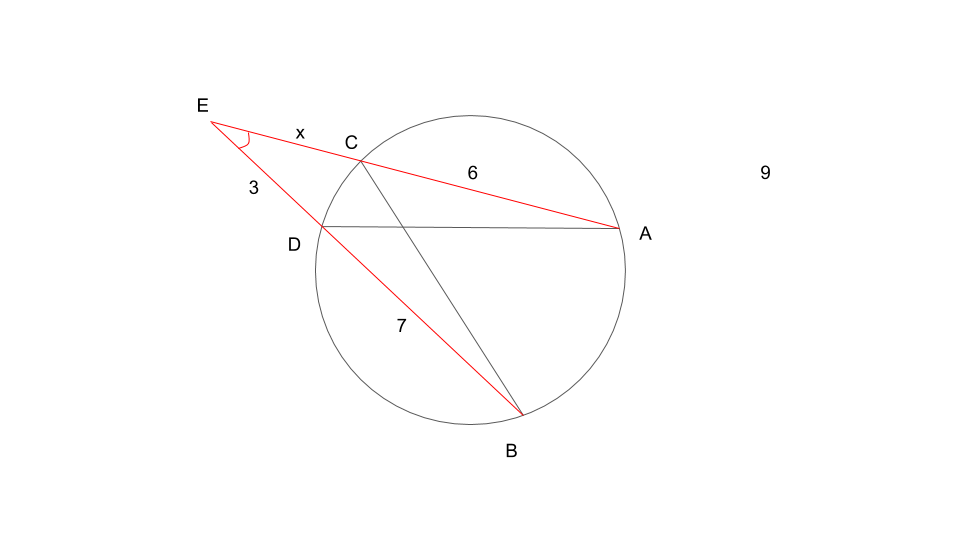
2つの角がそれぞれ等しい事がわかります(点Eの部分の角は△ADEと△BCEが共有しているので、当然等しいです)。これは相似条件を満たすという流れで示していきます!
円周角について△ADEと△BCEの角であることを示すために書き換えると、
∠CAD=∠EAD
∠DBC=∠EBC
より、
∠EAD=∠EBC …①
角を共有しているので、
∠DEA=∠CEB …②
①、②より相似条件を満たしているので、
△ADE∽△BCE
となります。
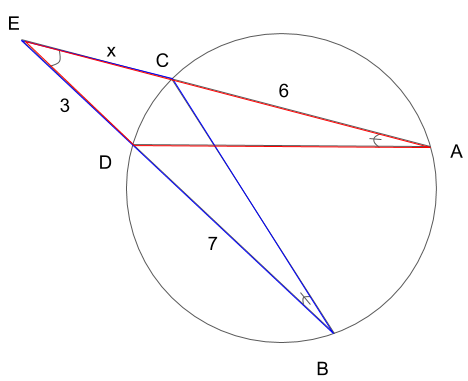
さて、ここから長さを当てはめて考えていくのですが、相似な図形同士が重なっていて見づらいと思うので、バラバラにして考えていこうと思います。
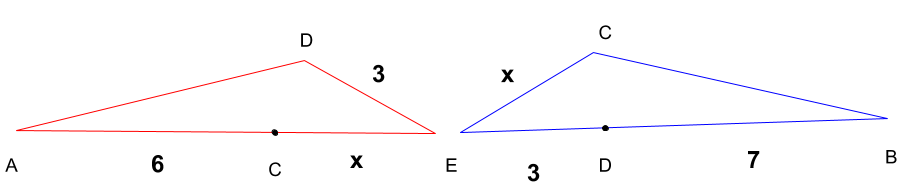
相似の性質より、長さの比は、
AE:BE=CE:DE
となるので、AE=AC+CE、BE=BD+DE注意して当てはめていくと、
\(6+x:(7+3)=3:x\)
\(6+x:10=3:x\)
という比の式が出来ます。これを計算すると、
\(x^{2}+6x-30=0\)
\(x=-3±\sqrt{39}\)
ここで、長さは正の数になるので、
\(x=-3+\sqrt{39}\)
となり、これが解となります。
このように、円周角の定理を利用することで、図形の長さを比によって解くことが出来ます。
まとめ
円に交わる線の長さの求める方針
- 円周角の定理を使う(使えるように線を追加する)
- 相似条件により、相似を導出する
- 図形の辺の比から長さを求め
いかがでしたか。円と三角形などの図形の関係は円周角の定理を用いることで求めることが出来る場合があります。
このような問題を解くときには、いかにして円周角を作るかという部分も大事ですが、
- どの図形に対して相似の関係を導けばいいか
- 比の計算に出てくる2次方程式等は解けるか
など、図形の読解力や計算力など、様々な数学力が必要です。もし足りない単元があると思ったら、戻って勉強してみると良いでしょう。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。