こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、図形の移動について解説します。
図形を動かすときに、ある事柄に注視して移動させることが数学ではよくあります。
この考え方はとても重要なので、しっかり理解して今後の内容に進めるように頑張っていきましょう。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
図形の移動とは?
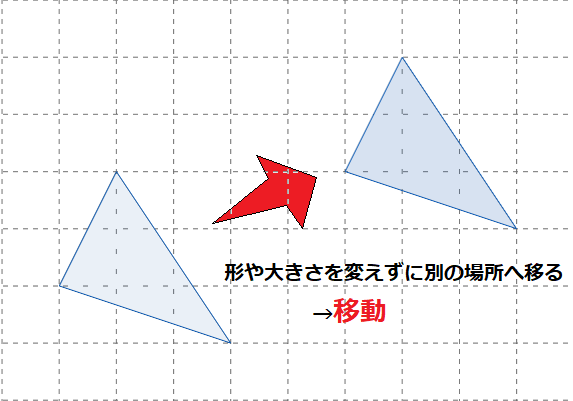
図形を移動したり、近くにある図形との関係を知るために必要な考え方の一つが「図形の移動」です。
その移動方法とはズバリ、
- 平行移動
- 回転移動
- 対称移動
の3つです!
この移動の際に、その図形の形が変わってしまったり、辺の長さや角度が変わってしまってはいけません。向きが変わったり、鏡写しのように反転してしまうのはOKです。
これを広く表すと、
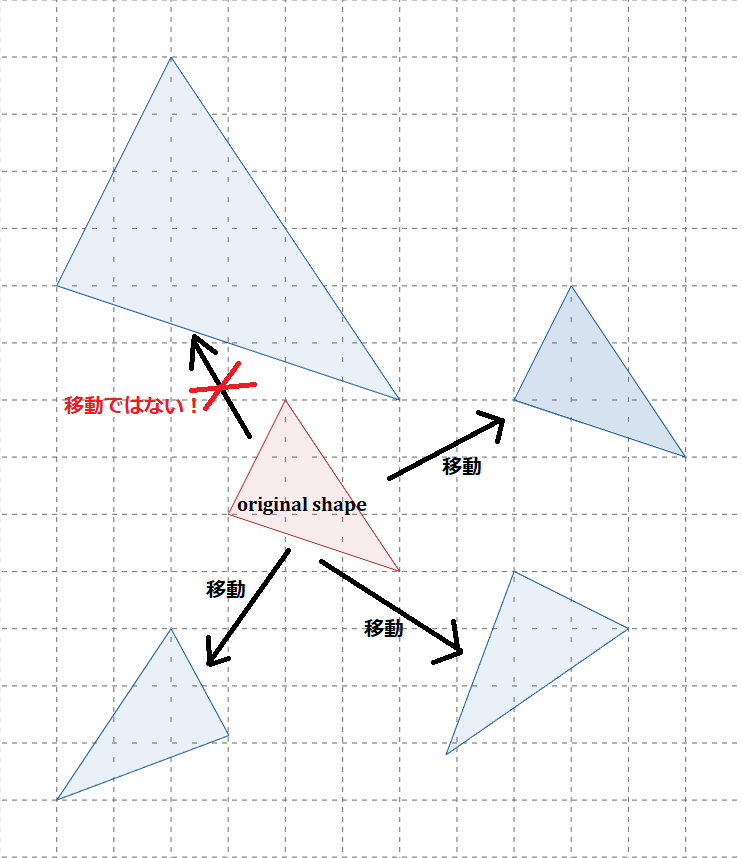
といった感じです。
さて、先程紹介した3つの移動方法ですが、これを勉強する為に「線」についての理解が必要なので、先に解説しておきますね!知っている人は飛ばしてもらってもOKです。
線とは
次の3つを覚えておきましょう。
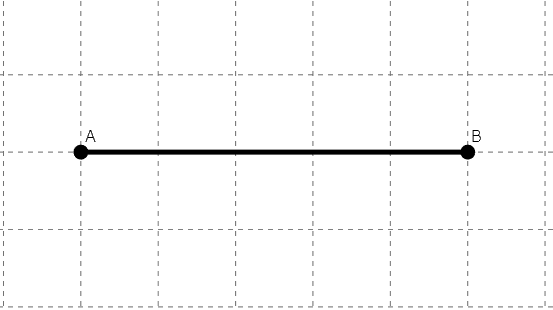
直線
直線とは、限りなく伸びている線のことです。
例えば、直線ABという場合、点Aと点Bの2点を通る、限りなく伸びる線です。

線分
線分とは、ある2点の間を最も短く結ぶ経路のことをいいます。
これは直線と異なり、永遠と伸びているということはありません。
例えば、線分ABがある場合、これは点Aと点Bを繋ぐ線で、その外側には出ていきません。
図形の線などは線分ということが出来ます。
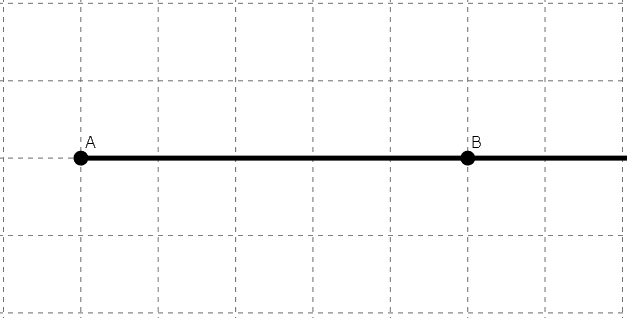
半直線
半直線とは、片方の点はからもう一点までは線分の性質で、そこから先は直線の性質をもった線です。例えば、半直線ABの場合、点Aから点Bが最短距離でつながっており、点Aから先ははみ出ていませんが、点Bから先は限りなく伸びている、という線になります。上二つに比べたら登場機会は殆どないと言っても過言ではありませんが、こういうものがあるんだと覚えておきましょう。
この3つを確認した所で、3つの移動について詳しく解説していきます!
平行移動
平行移動とは、図形を一定方向に一定の距離だけ動かす移動の事です。例えば、
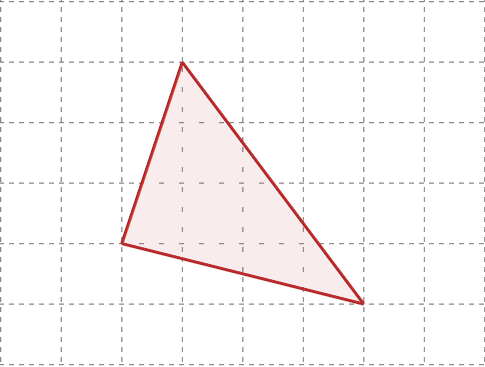
このような適当な図形があったときに、これを、
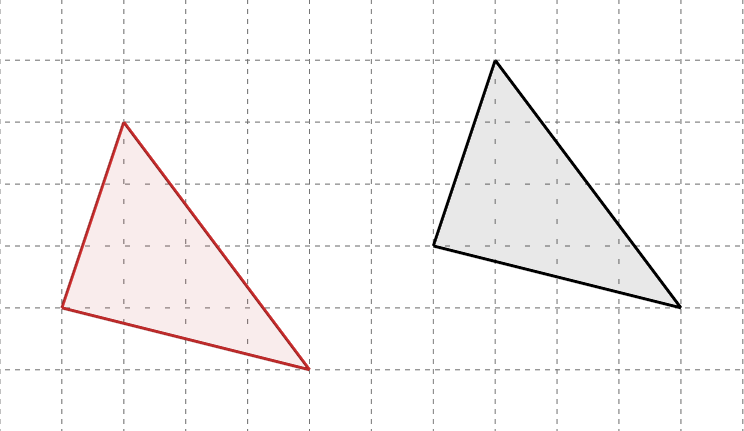
このように移動させたとします。移動した先で向きが変わっていないとしたら、これは平行移動したことになります。なぜなら、
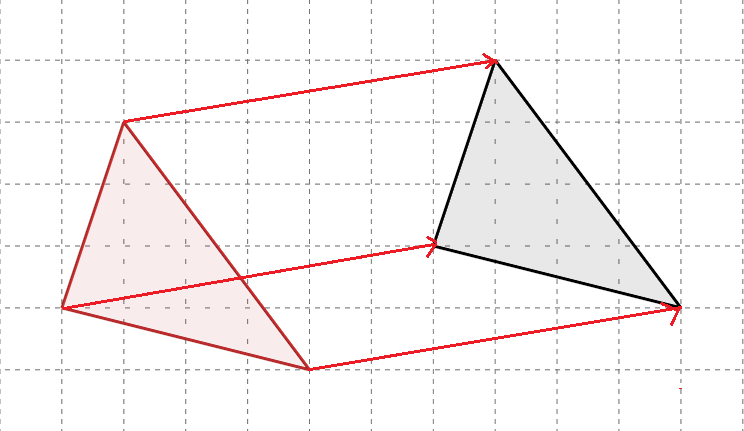
移動前と移動後の図形中の同じ位置を線で結ぶと分かりやすいのですが、
どの点について見てみても、同じ方向に同じ距離だけ動いている、ということが分かります。
この証明として、これが仮に少しでも向きが変わっているとすると、
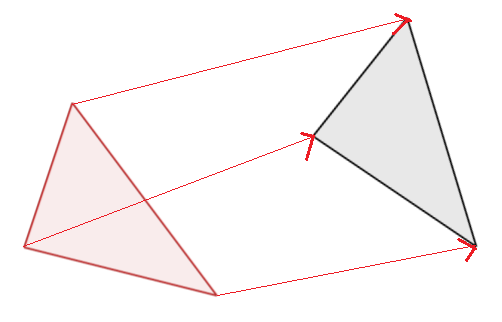
このように、それぞれの線の進む方向や進距離が少しずつ違ってしまいます。
点の位置によって移動した距離や向きが変わってしまうことが分かると思います。
ということで、向きが変わらず別の場所に移動したとき、その図形は平行移動をしています。
回転移動
回転移動とは、図形をある点を中心として一定の角度だけ回転させる移動の事です。例えば、
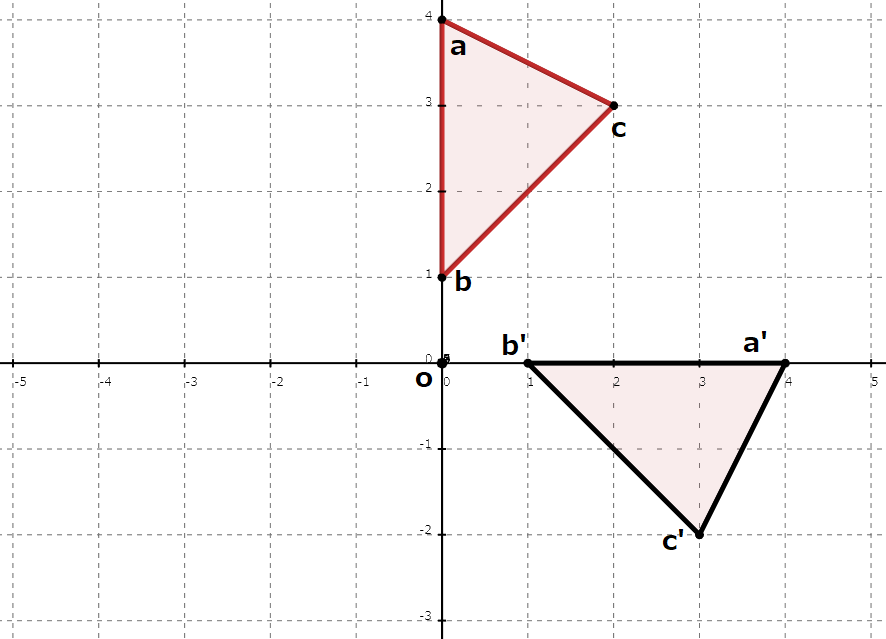
のような画像を見ると、図形の形や大きさは移動前と移動後で変わっておらず、向きが変わっているので平行移動ではないことが分かりますが、
この座標の原点を中心に右回りに回転させると、そのまま重ねることが出来そうです。
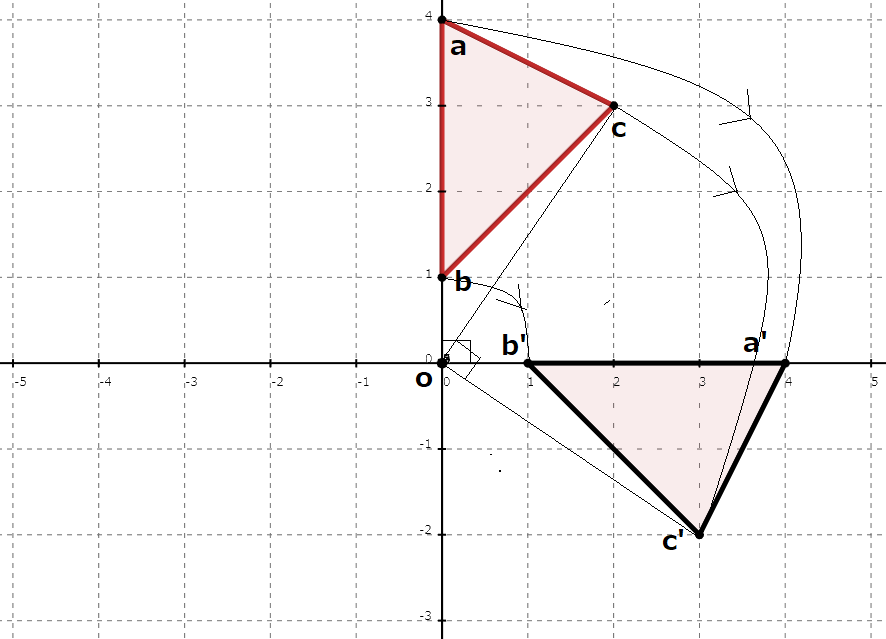
∠aoa’と∠bob’と∠coc’の角度を見てみると、どれも直角(45°)となっていることがわかります。
全ての点がある点を中心として、同じ角度だけ変わっていることから、この図形は回転移動をしたと断定できます。
このように、向きが違い、回転すれば重ねられるような場合は、どこかに中心があって回転移動することが出来ます。
さて、回転の際に、角度を取った基準となる点を回転の中心といいます。覚えておいてくださいね。
対称移動
平行移動で回転移動でも対応できない移動は、対称移動によって出来ます。
対称移動とは、図形をある直線を折り目として折り返す移動の事をいいます。
どんなものか図で表すと、
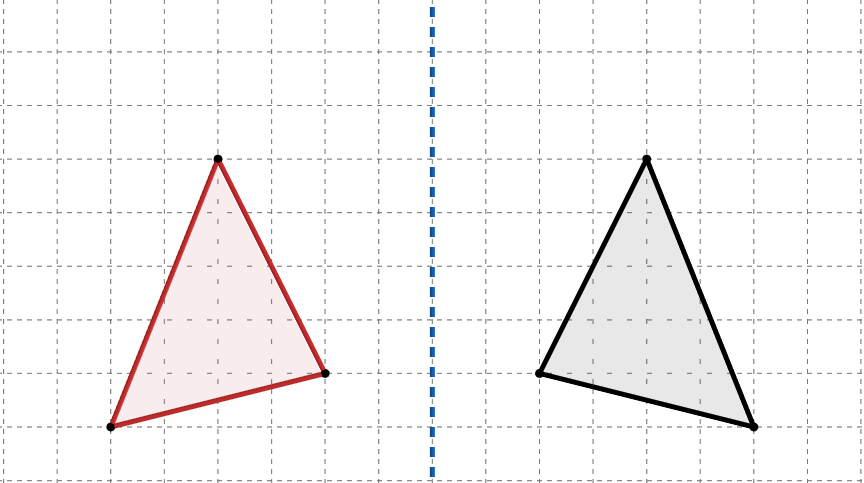
のような移動です。移動した図形は、他の移動と変わらず図形の形・大きさは変わっていません。回転移動や平行移動と違う点は、鏡写しとなっている点です。鏡写しの図形は、回転させても元々の図形と重ね合わせることが出来ません。平行移動も同様です。
ちなみに、この折り目の直線のことを対称の軸といいます。回転移動の方は回転の中心なので、間違えないように覚えてください。
移動前、移動後の図形の関係を表す方法
最後に、移動をする前と後の関係を表す方法について解説して終わろうと思います。
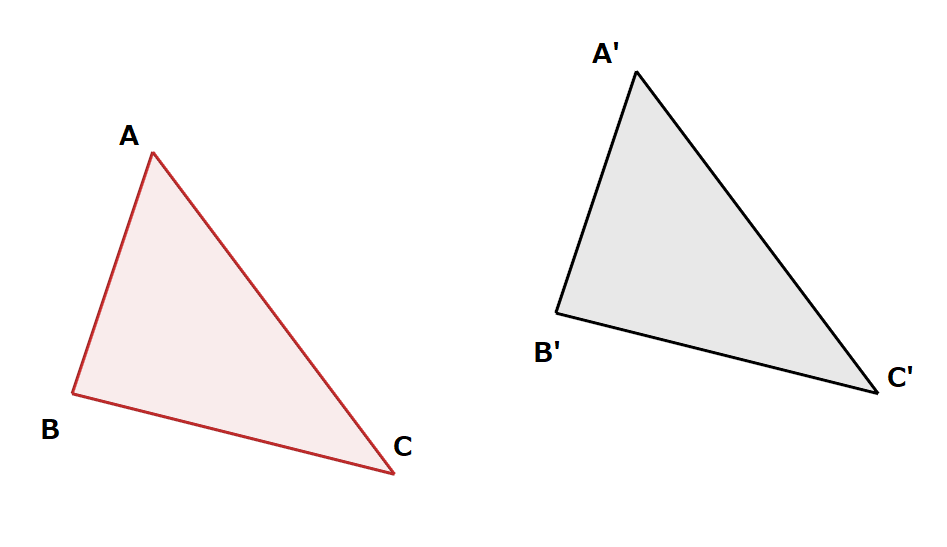
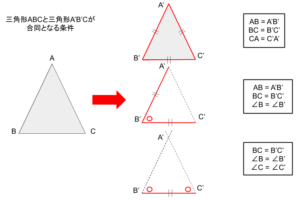
このような移動があったとします。移動なので、図形の形や大きさは同じままです。
移動前の三角形ABCと移動後の三角形A’B’C’の辺の長さが等しいことを数学的に表すとき、
AB=A’B’
BC=B’C’
CA=C’A’
のように表します。
【応用】合同な図形
今回の移動のように、図形の大きさや形が変わらずにある複数の図形の関係を互いに合同であるといい、合同な図形同士を≡で繋ぐことで表します。
例えば△ABCと△A’B’C’は合同ですから、
△ABC≡△A’B’C’
と表します。
(合同は中学2年で履修する内容になりますが、もし勉強したい方がいれば、こちらを読んでみて下さい。)
まとめ
- 平行移動(一定方向に一定距離だけ動かす移動)
- 回転移動(ある点を中心として一定角度だけ動かす移動)
- 対称移動(ある直線を折り目に折り返す移動)
今回は図形を移動するということを考えていきました。ただ移動するだけなのに様々な定義や用語が出てきて、難しく思えてしまう方もいるかもしれませんが、記事中で太字にした部分を追っていけば、要点は掴んでいただけるかと思います。
これから図形を勉強していく上での基礎になるので、しっかり抑えるようにしましょう!
やってみよう!
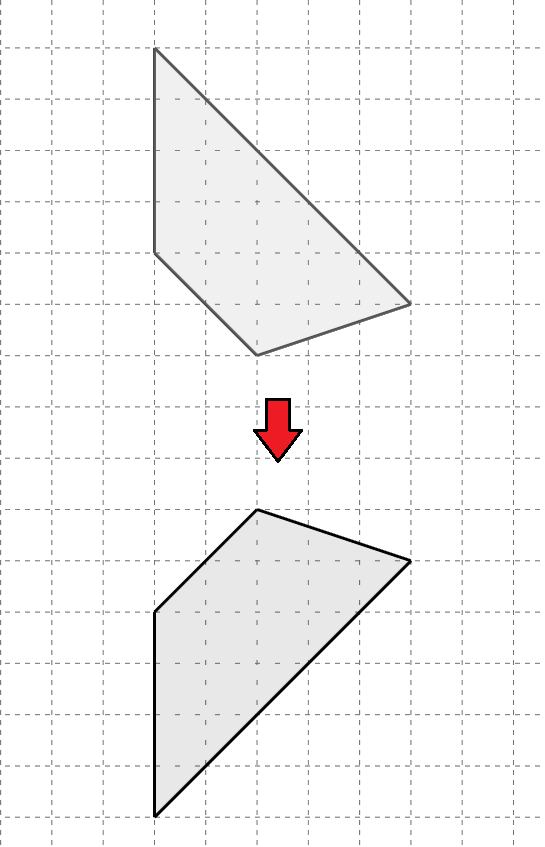
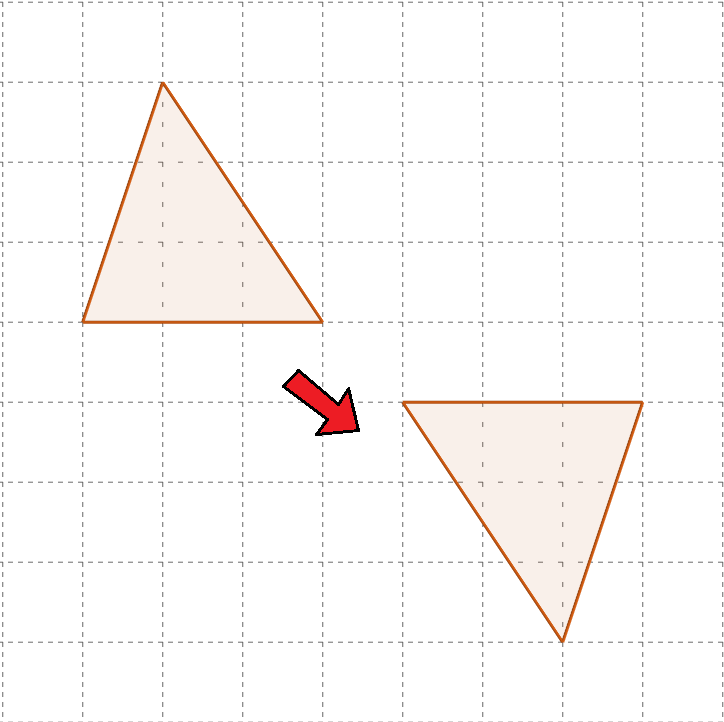
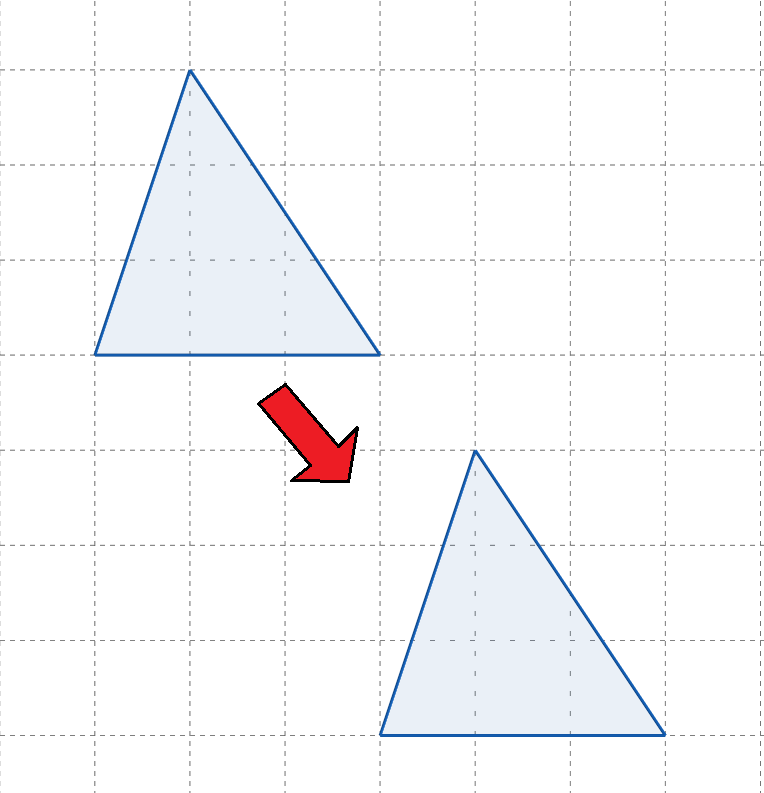
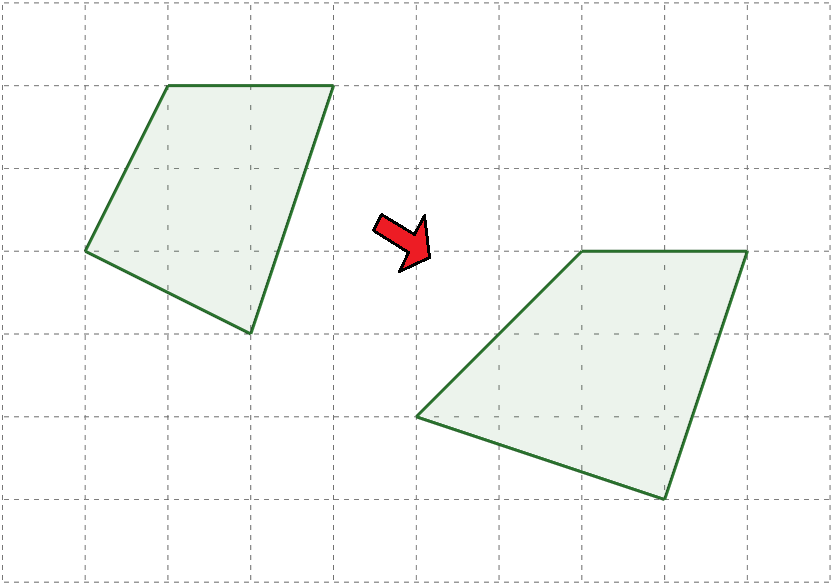
次の移動は「平行移動」「回転移動」「対称移動」「移動でない」のうちどれか、答えてみよう。
こたえ
- 対称移動
- 回転移動
- 平行移動
- 移動でない
最後までご覧いただきありがとうございました。 「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報! 数学の単元のポイントや勉強のコツをご紹介しています。 ぜひ参考にして、テストの点数アップに役立ててみてくださいね。 もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。