数学が苦手なお子さんの数は、中学でも高校でも、学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。今回は高校1年生の数学の中でも基本中の基本である式の計算について書いていきたいと思います。この単元はこの後の数学、物理などで必要になるので、しっかりと押さえておきたいですね。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
式の計算
今回書く「式の計算」という単元では、公式がたくさん出て来ますが、どれも基本中の基本である公式です。単純なものが多く、自分でもすぐに計算できるものが多いので、公式を全て暗記しようとするのではなく、実際に問題を解く時に使って身に付けていきましょう。
使う公式
この単元では様々な公式が出てきます。公式の数は多いですが簡単なものばかりです。恐れずにひとつひとつ見ていきましょう。
指数法則
指数とは何回その数をかけるかをその数の右肩に表しています。指数の計算のときに使える公式です。

上に3つ公式を紹介しましたが、自分で計算してみると当たり前であることが分かると思います。
2次の乗数公式、因数分解
文字式の2次式の公式です。左から右へが展開の公式、右から左へが因数分解の公式です。因数分解と聞くと難しそうに聞こえますが、因数分解はただ展開の逆をやっているだけです。恐れることはありません。
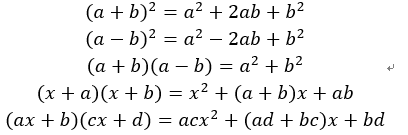
上には5つ紹介していますが、どれも計算すれば合っていることが分かると思います。5つも覚えたくないという人は、一番下さえ覚えてしまえば,自分で他の公式を導出できます。出てくる公式を全部覚える必要はありません。さらに問題を解いているうちに自然と身に付くものもあるので、公式を暗記することに必死にならなくても大丈夫ですよ。
3次の乗数公式、因数分解
文字式の3次式の公式です。左から右へが展開の公式、右から左へが因数分解の公式です。2次式よりも複雑になっていますが、基本的には2次式と変わりません。

絶対値
絶対値とは「ゼロからの距離」です。ゼロからどれだけ離れているかなのでプラスもマイナスもありません。この前提から公式がいくつかあるだけです。絶対値とはどのようなものかを理解しておけばここの公式は当たり前のものしかありません。
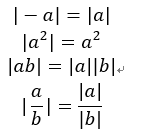
平方根
平方根とは2乗するとその中の数字になるといった記号です。
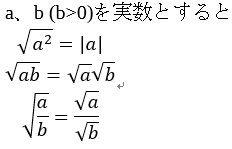
上の公式が成り立ちます。この公式も暗記するよりも平方根も絶対値と同じように、平方根とはどのようなものかを理解しておくことが大切です。
また、平方根の中に平方根がある「二重根号」というものも出てきます。式は複雑になりますが。二重根号に特別な性質があるわけではなく、平方根の性質を理解していれば大丈夫です。
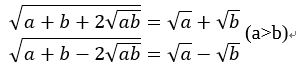
上の2つが公式としてありますが、因数分解して外側の平方根を取っただけです。難しいものではありません。
よくある例題
上の公式を使った例題をいくつか紹介していきます。
例題 (指数法則)
\((x^{3}y)^{3} \times x^{3}y^{2},(-3x^{3}y^{2})^{3}\)を計算せよ。
解答
\((x^{3}y)^{3} \times x^{3}y^{2}\\\\
=x^{3 \times 3}y^{3}\times x^{3}y^{2}\\\\
=x^{3\times 3+3}y^{3+2}\\\\
=x^{12}y{5}\)
\((-3x^{3}y^{2})^{3}\\\\
=(-3)^{3}x^{3\times 3}y^{2\times 3}\\\\
=-27x^{9}y^{6}\)
例題 (2次式)
\((2x+1)(x-3)\) を展開せよ。また、\(x^{2}-12x+32\) を因数分解せよ。
解答
\((2x+1)(x-3)\\\\
=2x^{2}+(2\times (-3)+1\times 1)x+1\times (-3)\\\\
=2x^{2}-5x-3\)
\(x^{2}-12x+32\\\\
=x^{2}+(-4-8)x+(-4)\cdot(-8)\\\\
=(x-4)(x-8)\)
例題 (絶対値)
\(|x+2|\)の絶対値記号を外せ。
解答
この問題では“場合分け”をする必要があります。それは絶対値記号の中が正の場合と負の場合で外し方が違うからです。
\(x<-2\) の時
\(|x+2|\\\\
=-(x+2)\\\\
=-x-2\)
\(x\geq 2\) の時
\(|x+2|\\\\
=x+2\)
このように絶対値の中が負になる時は絶対値を外すときにマイナスをつけなければいけません。
例題 (平方根)
\(\sqrt{(-3)^{2}},\sqrt{8}+\sqrt{18}-\sqrt{2}\)を簡単にせよ。
解答
\(\sqrt{(-3)^{2}}=\sqrt{9}=3\)
\(\sqrt{8}+\sqrt{18}-\sqrt{2}\\\\
=\sqrt{4}\cdot \sqrt{2}+\sqrt{9}\cdot \sqrt{2}-\sqrt{2}\\\\
=2\sqrt{2}+3\sqrt{2}-\sqrt{2}\\\\
=4\sqrt{2}\)
平方根の足し算では中が同じものだけをまとめることが出来ます。また、負の数を2乗したからといって、平方根は負にはなりません。
苦手克服法
よくある悩み
中学ではほとんどが「数字」でしたが、高校では「文字」が多く出てきます。この「式の計算」は高校生になって最初に習う単元なので、この文字だらけの数学に拒否反応が出てきてしまうかもしれません。
そんなあなたは
高校の数学の公式や定理は文字を使って表されます。しかし、しっかりと公式や定理を理解していれば難なく解くことができます。教科書をしっかりと読み、自分で考えれば分かる内容です。逃げずに考えてみましょう。
式と計算の攻略
この単元は高校に入って最初の単元です。そんなに証明の難しい公式や定理は出てきません。公式や定理はただそれを暗記するのではなく、その公式や定理を説明できるようになりましょう。この単元の内容は後から何度も出てくるので内容をしっかりと理解しましょう。