数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。今回は高校1年生の数学の中でも2次関数の中でも、判別式・不等式について書いていきたいと思います。2次関数は数学はもちろん、物理などでも使うのでしっかりと押さえておきたいですよね。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
2次関数とは
yがxの2次の多項式で表すことのできるとき、yはxの2次関数であるといいます。式で書くと、
\(y={ax}^2+bx+c\)
という形です。
判別式とは
判別式とは、2次方程式の係数を用いた、実数解の個数を判別できる式のことです。判別式Dは\(y={ax}^2+bx+c\)の係数を用いて、
\(D=b^2-4ac\)
と表されます。判別式は、2次方程式の解の公式\(x=\frac{-b^2±\sqrt{b^2-4ac}}{2a}\)のルートの中身です。この判別式Dが正であれば、実数解の数は2個、判別式Dがゼロであれば、プラスでもマイナスでも解が一緒になるので、実数解は1個、判別式Dが負であれば、ルートの中身が負になるので虚数解となるので、実数解の数は0個となります。
この判別式を使うと、2次関数と直線との交点を求めることができます。2次方程式は2次関数と直線\(y=ax\)の連立方程式と考えられるので、判別式Dを使うと2次関数と直線の交点の個数を求めることができます。
2次不等式
2次関数の分野で判別式を使って解くのは2次不等式です。2次不等式の解が存在するかどうかは判別式を使うことによって判断できます。また、2次不等式を解くときに1番分かりやすい方法は、2次関数のグラフを描き、グラフから求めるxの範囲を求めるという方法です。2次不等式は平方完成をしてグラフを求めたり、因数分解してx軸との交点を求めたりと様々な解き方があるので、いろいろ試してみると様々な解き方が身に付きますよ。
よくある例題
2次関数についての例題をいくつか紹介していきます。
例題 (共有点の数)
2次関数\(y=3x^2+6x+k\)のグラフとx軸との共有点の数は\(k\)の値によってどのように変わるか。
解答
与えられた2次関数の判別式を考えると、
\(D=6^2-4⋅3⋅k=36-12k\)
異なる2つの共有点を持つ場合、\(D>0\)であるので、
\(36-12k>0\)
\(k<3\)
2次関数が直線に接する(共有点1つ)場合、\(D=0\)
\(36-12k=0\)
\(k=3\)
共有点を持たない場合、\(D<0\)
\(36-12k<0\)
\(k>3\)
よって、与えられた2次関数とx軸の交点は、k>3 の時、共有点0個、k=3の時、共有点1個、k<3の時、共有点2個である。
例題 (放物線と直線の共有点)
放物線\(y=-x^2+7x+12\)と直線\(y=-x-8\)の共有点の座標を求めよ。
解答
与えられた放物線と直線の式から、
\(-x-8=-x^2+7x+12\)
\(x^2-8x-20=0\)
\((x-10)(x+2)=0\)
よって、共有点のx座標はx=10, -2なので、求める共有点のy座標は、x=10, -2 を代入して、
\(y=-10-8=-18\)
\(y=-(-2)-8=-6\)
よって、求める共有点の座標は、( 10, -18 )、( -2, -6 ) となります。
例題 (2次不等式)
2次不等式\(2x^2≤6x\)を解け。
解答
与えられた2次方程式から、
\(2x^2≤6x\)
\(2x^2-6x≤0\)
\(2(x^2-3x)≤0\)
\(2(x-\frac{3}{2})^2-\frac{9}{2}≤0\)
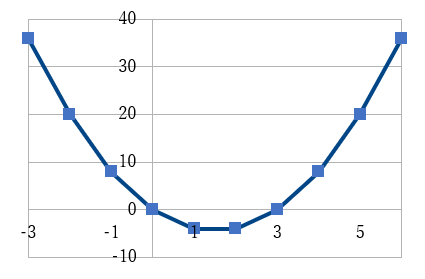
グラフは上の図のようになり、与えられた2次不等式の解は、
\(0≤x≤3\)
となります。
この分野が苦手な人
2次関数の中でも、この判別式や2次不等式の分野の問題が解けない人は、問題を与えられて何をしたらいいか分からない人が多いと思います。この分野の問題では、問題文から判別式を使うことが分からないことが多いです。関数と関数の共有点という言葉が出てきたら「判別式を使うかも」と考えるようにしましょう。
1つの解き方をこだわらない
この判別式・不等式の分野の問題は、1つの問題に対して解く方法はたくさんあります。同じ問題でも人によって解き方は違うので、他の人と違う解き方だからといって悪いというわけではありません。いろいろな解き方で解けるようになった方が、解ける問題は多くなるのでいろんな解き方にチャレンジしていきましょう。