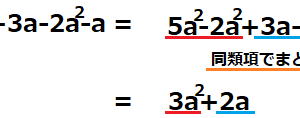こんにちは、あすなろスタッフのカワイです。
前回は、文字と式の表し方のルールを説明しました。今回は、式の中に文字を置き換える「代入」について解説をしていきます!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
代入ってなに…?
「代入」とは、式の中の文字に数字を入れることを言い、代入によって出てきた値のことを「式の値」といいます。
計算のプロセスは3段階になります。
- 式に省略した記号を戻す
- 文字を数字と置き換える
- 計算する
いくつか例題をあげるので、一緒に考えてみましょう!
例題1
$$a=3のときの4aの値$$
まず、4aを4×aという形に直します。(分かるようになってきたら直さなくても良いです!)
$$4a=4×a$$
次に、a=3なので、aのところを3に置き換えます。
$$4×a=4×3$$
あとは簡単ですね。4×3をすればいいので、式の値は12となります。
例題2
$$b=-2のときの-5bの値$$
次は-が入ってきますから、注意が必要です!
まず、-5bを(-5)×bという形に直します。
$$-5b=(-5)×b$$
次に、b=-2であるので、bのところを-2に置き換えます。
$$(-5)×b=(-5)×(-2)$$
$$(-5)×(-2)=10$$
このような形で計算していきます。
例題3
$$y=\frac{1}{3}のときの1-2yの値$$
代入する値が分数の場合も、基本的にやることは同じです。
$$y=\frac{1}{3}を代入$$
$$1-2y$$
$$=1-2×y$$
$$=1-2×\frac{1}{3}$$
$$=1-\frac{2}{3}$$
$$=\frac{1}{3}$$
実際の計算のように記述してみました!分数に直すところを気を付けて書いていく形になります。
例題4
$$x=\frac{1}{2}のときの\frac{1}{x}の値$$
応用問題をひとつ解いてみましょう。ここまでついてくることができた方なら大丈夫です!
まずを÷を含めた式に変えていきます。
$$\frac{1}{x}=1÷x$$
次に、xに値を代入します。
$$x=\frac{1}{2}を代入$$
$$=1÷\frac{1}{2}$$
割り算の形だと計算がしにくいので、積の形に直していきます(この時に項は逆数の値に変わります!ここを間違えないように注意!)
$$=1×2$$
×に変えると、途端に小学生の頃に習った計算になってしまいました。
従って
$$\frac{1}{x}=2$$
となります。
まとめ
代入とはなにか分かっていただけましたか?計算手順を今一度確認してみましょう。
- 代入する前に、計算記号を戻して、
- 値を代入して、
- 計算する
一番間違えやすいのは代入ではなく③の四則計算をするところになります。 もし、計算ミスをよくしてしまうという方は、計算の仕方を復習してみるとかなりミスが減るはずです。 これらの一通りの流れはなかなか難しいかもしれません。ですが、やっていくとだんだんコツが掴めて、いつかは楽々解けるようになっていきます。頑張っていきましょう!
やってみよう!
問題
- $$y=4のときの3y-1$$の値を求めてみよう。
- $$x=-3のときの2-4x$$の値を求めてみよう。
答え
- $$3y-1=3×4-1$$ $$=11$$
- $$2-4x=2-4×(-3)$$ $$=14$$
最後までご覧いただきありがとうございました!
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
数学は単元の繋がりが強い教科なので、「わからない!」となったら早めに戻り学習をするのが苦手克服の近道です。
家庭教師のあすなろ関西では、学校の教科書を中心とした予習・復習を軸に、独自の「あすなろ式ラクラク定着法」を用いて指導をしています。
勉強のやり方にお悩みの方・自分に合った勉強法を見つけたい方は、無料の体験授業でお気軽にお試しくださいね!