こんにちは、あすなろスタッフのカワイです。
今回は、点が分かっている時や、グラフが分かっている時に式を導出する方法について解説していきたいと思います。
関連記事:【中2数学】一次関数ってなに?比例とどう違うのか、解説します!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
2点が分かっている時の1次関数の式の求め方
2点が分かっている時の求め方と上に書きましたが、比例のときは、グラフ上の1点が分かっていれば、式を導出することが可能でした。
しかしながら、1次関数の場合は1点だけでは式を導くことができません。
それはなぜでしょうか?
2点分からないと1次関数を求められない理由
1次関数は直線になるという事を理解している前提で話していきますね。
例えば、このような点が1点あったとします。
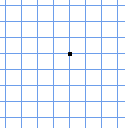
この点を通る直線を考えると、
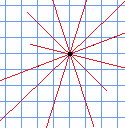
無限に書くことができてしまいます。一次関数は1つの式、すなわち一本の線に決まらないといけないので、このようにいくつも引けてしまってはいけませんね。
次に2点があるとどうでしょうか。
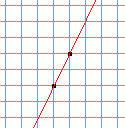
直線はこの1本しか考えられないはずです。
このような理由から、2点無いと式を求めることができないのです。
あれ?では、どうして比例のときは1点で求めることが出来たの?
と思う人がいるかもしれません。
それは、比例の場合、定義で「原点\((0,0)\)を通る」とあり、比例の関数である時点で1点\((0,0)\)が決まっているからです。適当な1点と\((0,0)\)があれば、比例の場合は式を求めることが出来ます。
では、話を戻しましょう。
例 \((3,2)\)と\((6,6)\)を通る一次関数の式を導出してみよう
2点あるので、式を導くことが出来そうですね。
一次関数\(y=ax+b\)を求める上で必要なのは、
- 傾き\(a\)
- 切片\(b\)
の2つです。まず傾きから考えていきましょう。
傾きを求める
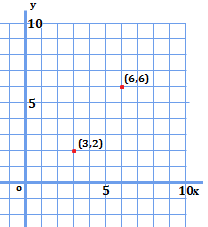
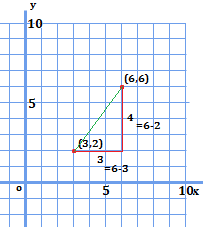
分かりやすいように座標をグラフに示してみました。
次に、\(x\)座標と\(y\)座標の変化を表でそれぞれ見ていくと、
| y | 2 | → | 6 |
| x | 3 | → | 6 |
このようになっています。\(x\)が\(3\)増えると、\(y\)が\(4\)増える、ということが分かります。
傾きというのは「\(x\)が1増えるときの\(y\)の増減量」から求められるので、変化量同士で割ってみると、傾きが出てきそうです。
これより、傾きは\(\frac{4}{3}\)であると分かりました!
このように$$\frac{yの変化量}{xの変化量}$$で表されるものを変化の割合といい、これで導かれたものは、傾きを表します。
切片を求める
傾きが分かったので、次は切片を求めていきましょう。
傾きを\(y=ax+b\)のうち\(a\)のところに代入して、
$$y=\frac{4}{3}x+b$$
となります。この式が上に示した2点を通ればいいので、2点のどちらかの座標を入れてあげます。\((3,2)\)でも\((6,6)\)でも解くことが出来ますが、今回は\((3,2)\)で解いていくことにします。
(式に両方の点を代入する必要はありません。2点間の傾きを求めてあるので、片方の点が通る切片\(b\)が見つかれば、もう片方も通ることになります。)
\(y=\frac{4}{3}x+b\)に\(x=3\)、\(y=2\)を代入して計算を進めていくと、
$$2=\frac{4}{3}×3+b$$
$$2=4+b$$
$$b=-2$$
となります。これで切片を求めることが出来ました。
従って、\((3,2)\)と\((6,6)\)を通る1次関数の式は
$$y=\frac{4}{3}x-2$$
です。
(応用)連立方程式から式を導出する
1次関数の式は、傾き\(a\)と切片\(b\)を求めることが出来れば、1つに決めることが出来ると分かったと思います。また、1点が分かっているとき、それを通る式は無限にあると説明しました。
そのような点が2点あるとき、それぞれ1点に考えられる式の可能性のうち、2点で傾きと切片が完全に一致する値が1つだけ見つかるということになります。
この考え方というのは、連立方程式での解き方に非常に似ています。
従って、傾きと切片は連立方程式の形で解くことが出来ます。
\(y=ax+b\)の\(x\)と\(y\)に2点の値を入れて、2つの式を作ります。
\begin{eqnarray}\left\{ \begin{array}{l}2=3a+b\\6=6a+b\end{array}\right.\end{eqnarray}
これらを連立方程式と同じように解いていきます。下式を変形して
$$b=6-6a$$
これを上式に代入すると
$$2=3a+6-6a$$
$$2=6-3a$$
$$3a=4$$
$$a=\frac{4}{3}$$
と、傾きが求められました。
この傾きを用いて、
$$b=6-6×\frac{4}{3}$$
$$b=6-8$$
$$b=-2$$
と切片が求められました。
この方法では、切片か傾きのどちらかが分かっていれば、もう一方をすぐに求めることが出来るなど、便利な場合が多いです。
ただ、この方法で解く前に、何故これで解くことが出来るのかを先に理解するようにしてください(意味を理解せずに解いてしまうと、応用がきかなくなってしまいます!)。
まとめ
- 2点が分かれば1次関数の式を解くことが出来る!
- 傾き・切片を求めることで式が求められる!
- 変化の割合は\(\frac{yの変化量}{xの変化量}\)で求められ、その値が傾きとなる!
- 連立方程式を用いて解くこともできる!
2点が分かっていれば式を求められるので、式の分からないグラフがある場合、グラフから2点を読み取ることが出来れば、式を求めることも出来ます!
練習問題に挙げておくので、余裕があれば解いてみて下さい!
やってみよう
1.\((1,6)\)と\((3,2)\)を通る一次関数の式を導出してみよう
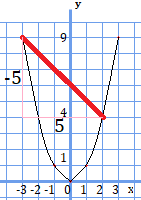
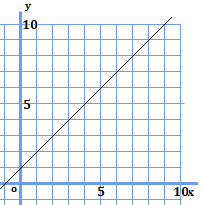
2.以下の1次関数のグラフから式を導出してみよう
こたえ
-
\(y=-2x+8\)
解説:まず傾きを求める。変化の割合\((=\frac{yの変化量}{xの変化量}=a)\)より、$$a=\frac{2-6}{3-1}$$$$a=\frac{-4}{2}$$$$a=-2$$より、傾きは\(-2\)とわかる。傾きを\(y=ax+b\)に代入すると、$$y=-2x+b$$となり、これに\((1,6)\)を代入すると$$6=-2×1+b$$$$b=8$$となる。従って、式は\(y=-2x+8\)となる。 -
\(y=x+1\)
解説:グラフを見ると、\((0,1)\)、\((1,0)\)を通っていることが分かる(他の2点でもOK)。これらより傾きを求める。変化の割合\((=\frac{yの変化量}{xの変化量}=a)\)より、$$a=\frac{0-1}{1-0}$$$$a=-1$$より、傾きは\(-1\)とわかる。傾きを\(y=ax+b\)に代入すると、$$y=-x+b$$となり、これに\((0,1)\)を代入すると$$b=1$$となる。従って、式は\(y=-x+1\)となる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。