こんにちは、あすなろスタッフのカワイです。
本記事では、中学1年生の頃に勉強した「比例」の考えを拡張した「1次関数」という単元の触りについて解説していきます。
比例の内容が不安な方は、先に「比例」を復習してから読んでいくと理解しやすいかもしれません!
では、頑張っていきましょう!
関連記事: 【中1数学】比例ってなんだろう?どういう時に必要になるのか、解説します!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
1次関数とは?
\(y\)が\(x\)の1次式で表すことが出来るとき、\(y\)は\(x\)の1次関数である、といいます。
式の形で表すと、\(y=3x\)や\(y=-2x+5\)のようなものです。
ここでいう\(y=3x\)は中学1年の数学で「比例」として学習しましたが、1次関数は\(y=-2x\color{red}{+5}\)のように、定数項(文字を含まない項)がある式も含んでいます。
(復習)1次式とは?
1次式とは、式中の一番大きい次数が1の関数のことをいいます。
$$y=4x$$
は1次式ですが、
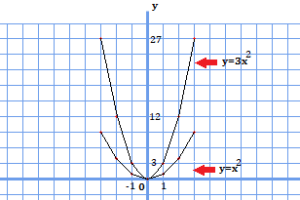
$$y=4x^{2}+3x$$
は一番大きな次数が2となるので、1次式ではありません。
では、1次式の考え方が分かる例について考えていきましょう。
例1.容器の水の量と時間の関係
元から10Lの水が入っている容器に、1分間に水を3Lずつ入れていくとき、容器の水の量と時間はどのような関数で表されるか?また、どのようなグラフとなるか?
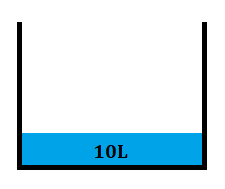
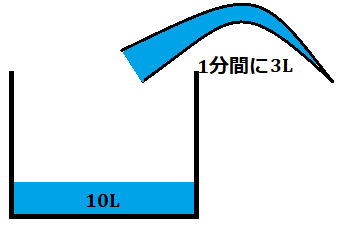
元から10Lの水が用意されていて、
水が1分間に3Lのペースで入っていくという状況を考えたいということです。時間を\(x\)、容器の水の量を\(y\)としたとき、これらの値はどのように変化していくでしょうか。
考えやすくするために、表で表してみましょう。
| 時間 | \(0\) | \(1\) | \(2\) | \(3\) | … |
| 容器の水の量 | \(10\) | \(13\) | \(16\) | \(19\) | … |
このように表すことが出来ますね。
次に、仮に容器の水が最初から無い場合も考えてみましょう。水が1分間に3Lのペースで増えていくので、
| 時間 | \(0\) | \(1\) | \(2\) | \(3\) | … |
| 容器の水の量 | \(0\) | \(3\) | \(6\) | \(9\) | … |
と表すことが出来ます。これは、比例で学習したように、$$y=3x$$で表すことが出来ますね。
さて、上の表を見比べると、このように見ることができると思います。
| 時間 | \(0\) | \(1\) | \(2\) | \(3\) | … |
| 容器の水の量 | \(0\color{red}{+10}=10\) | \(3\color{red}{+10}=13\) | \(6\color{red}{+10}=16\) | \(9\color{red}{+10}=19\) | … |
時間で増えていく3Lと、時間に関係なく常にある10Lの足し合わせと考えると、非常に都合が良いということに気づけると思います。
従って、時間と比例して増える$$y=3x$$という要素に、時間によらずあり続ける$$y=10$$という要素を足し合わせるので、これを式で表すと、
$$y=3x+10$$
となります。
この値自体は、最初の問題文に出てきた数字しかないので、意味を理解さえすれば実はそこまで難しく考えなくても解くことができるというわけです。
1次関数のグラフを書いてみよう
今度はこの例をグラフで表してみようと思います。
\(y=3x+10\)の式の\(x\)に好きな数字を入れて、表を作成すれば書きやすいですが、式を書く前にさきほど表を出したので、その表を用いて座標に点をプロットして線で繋いでいきます。
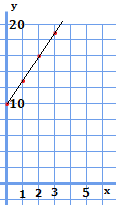
すると、このようになりました。\(x\)が\(0\)の時に\(10\)となっていて、\(x\)が増えると、直線的に値が増えています。
時間に関わらず、値が常に10ある、という事以外は変わらないので、比例のグラフとそっくりのグラフとなっています。
比較のために、\(y=3x\)のグラフを示してみますね。
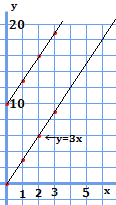
確かに、\(y=3x+10\)のグラフは、\(y=3x\)に比べ、常に\(10\)上の値を取り続けています。
従って、\(y=ax+b\)という式があったときに、\(a\)というのは比例と同様に傾きを表し、\(b\)というのは\(x=0\)のときの\(y\)を表していることになり、この値のことを切片とよびます。
今回の式\(y=3x+10\)では、\(3\)が傾き、\(10\)が切片を表しているという事になります。
まとめ
- 一次関数の式\(y=ax+b\)は、\(y\)が\(x\)に依る\(y=ax\)と、\(y\)が\(x\)に依らない\(y=b\)の足し合わせである。
- \(y=ax+b\)のうち、\(a\)は傾き、\(b\)は切片(\x=0\)のときの\(y\)の値)を示す。
一次関数とは何か、一言で表すと、「比例関係+常に変わらない値」で表される関数という事になります。
比例関係さえ理解できていれば、一次関数も意外と簡単に解けてしまうという事が分かればOKです。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。