こんにちは、家庭教師のあすなろスタッフのカワイです!
今回は2次方程式を因数分解の考えを用いて解く方法を解説していきたいと思います。
これまで数学記事で様々な2次方程式を解いてきましたが、今回の解き方を習得したら、中学で勉強する2次方程式の解き方は完璧です!
因数分解を忘れてしまった人向けに復習できる内容を含んでいるので、因数分解が不安な方も是非最後まで読み進めてみて下さい!
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
【おさらい】因数分解とは?
因数分解とは、多項式をいくつかの因数の積として表したものとなり、展開の逆の処理となります。どういうことかというと、

上の図を見てもらうと何となく関係がわかると思いますが、因数分解されたものを展開するのは、分配法則でかけ算を繰り返すだけなので比較的簡単ですが、逆の因数分解はというと、知っていないと解けない部分があります。
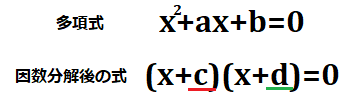
上図のように、多項式と因数分解をした式を決めたとき、これらが恒等式となるには、
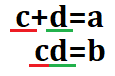
という関係を満たす必要があります。逆に言えば、上の形の2次方程式であれば、\(a\)や\(b\)にはどんな実数が入ってもいいので、因数分解をすることが出来ます!(公式として覚えておいてもいいでしょう!)
例えば、\(x^{2}+3x+2\)という多項式を因数分解したいとき、上の式と見比べてみると、\(a\)は\(3\)、\(b\)は\(2\)にあたります。これを公式に当てはめると、
\(c+d=3\)
\(cd=2\)
となります。これに当てはまる値を考えると、
\((c,d)\)は\((1,2)\)もしくは\((2,1)\)となります(どちらでもOKです!)。
これを因数分解後の式に当てはめると、
\((x+1)(x+2)=0\)
となります。このように、上の式に当てはめて解いてもらうと、因数分解をすることが出来ます!
\((x+a)(x-b)=0\)はどうやって解く?
さて、因数分解を軽くおさらいしたところで、
\((x+a)(x-b)=0\)
はどうやって解くか?ということですが、今のところよくわからないので、解の公式で解いてみることにします。
\((x+a)(x-b)=0\)
\(x^{2}+(a-b)x-ab=0\)
これを解の公式で解くと、
\(x=\frac{-(a-b)±\sqrt{(a-b)^{2}+4ab}}{2}\)
\(x=\frac{-a+b±\sqrt{(a+b)^{2}}}{2}\)
\(x=\frac{-a+b±(a+b)}{2}\)
とすると、
\(x=b\)と\(x=-a\)
が求まります。
何か、かなりスッキリした答えになりました。
さて、何か気づくことはありませんか…?
実は、最初の因数の積の形の中身の値と同じになっています。(最初から分かっていた人はすごい!)
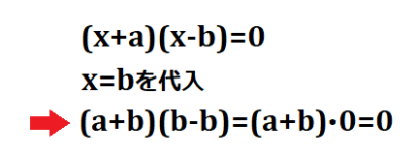
式に解である\(b\)を代入すると、確かに打ち消されて、\((x-b)\)の因数が打ち消されて\(0\)になります。\(-a\)を入れても同じような形で\(0\)になります。
長々と説明しましたが、結局は2つある()を消すことが出来る数字を入れてあげれば、解が得られるということです!
例1.\((x-3)(x+5)\)
上の説明を読んだらもう説明することはないかもしれませんが、一応解きましょう!
\((x-3)\)を\(0\)にするために\(x\)に入れる値は何かというと、\(3\)ですね。
\((x+5)\)を\(0\)にするために\(x\)に入れる値は何かというと、\(-5\)です。
従って、
\(x=3,x=-5\)
となります。
式を見た瞬間に答えがわかってしまいますね。
例2.\(x^{2}+4x-5\)
これは解の公式を用いてといてもいいですし、因数分解をして解いてもいいです。
今回は因数分解で解いていきましょう。
上の式を因数分解するときに、
\((x+a)(x+b)=0\)
を目標とすると、
\(a+b=4\)
\(ab=-5\)
と置くことが出来ます。これを解くと、
\((a,b)=(1,-5)\)
または
\((a,b)=(-5,1)\)
となります。従って、この多項式は、
\((x-1)(x+5)=0\)
となります。
ここまで来たら、後は例1と同じなので大丈夫ですね。
答えは
\(x=1,x=-5\)
となります。
まとめ
- 因数の積の形において、\(x\)に代入してカッコ内を\(0\)にできる値が解になる!
やってみよう!
次の方程式の解を求めてみよう
- \((x+4)(x-6)=0\)
- \(x(x+8)=0\)
- \(x^{2}-4x+3=0\)
- \(x^{2}+6x+9=0\)
こたえ
- \(x=-4,x=6\)
- \(x=0,x=-8\)
- \(x=1,x=3\)
- \(x=3\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。