こんにちは、家庭教師のあすなろスタッフのカワイです。
日々生活していると、四角形のテレビがあったり、六角形の鉛筆があったり、様々な形を見かけることができます。さて、皆さんはそれらの特徴について何か考えたことはありますか?
実は、図形には面白い数学的特徴が沢山あるんです!
その中でも、今回は角度に注目して、多角形の角の数によってどんな特徴があるのかを探っていきたいと思います!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
わからない…を“わかる!”に変える家庭教師
「勉強がわからない」そんな悩みは、あすなろ関西の家庭教師が解決!一人ひとりに合った勉強方法で、小学生から高校受験までサポート!
たった15分の勉強で、これまでの3倍の効果を実感!そんな効率的な学びを、無料体験で試してみませんか?

=もくじ=
多角形・外角・内角とは?
多角形とは、角が3つ以上ある平面図形のことを言います。(ここでの多角形は、すべての角が180°よりも小さい角であるものとします)
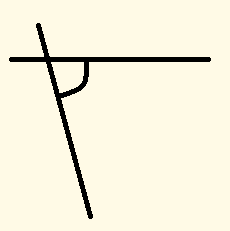
角というのは、直線や線分が交差した点と、その両端の線で挟まれた部分のことを言います。
多角形はどのように区別がされているかというと、この角の数によってされています。
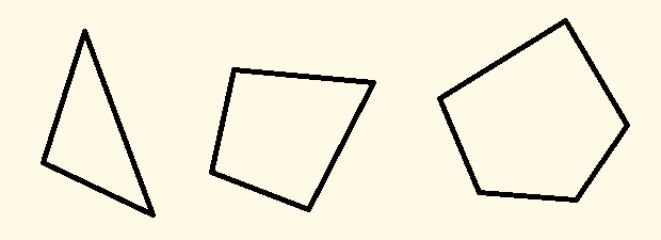
左から「三角形」「四角形」「五角形」です。
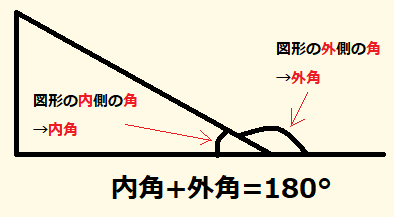
また、図形の内側の角を内角といい、それから延長した辺と1辺がつくる角を外角といいます。この2つの角度を足すと180°になります。
多角形の内角の和を測ってみよう!
三角形・四角形の内角の和は小学校で習ったと思いますが、それぞれ180°、360°です。さて、五角形、六角形など、角の数が増えていったら、内角の和はどうなるでしょうか?
これを求めるために、三角形の内角が180°というすでに分かっていることを利用することで、わざわざ分度器などを用いなくても知ることが出来ますよ!
四角形を例に考えてみましょう。
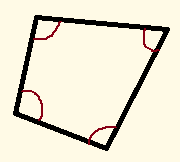
四角形の内角の和が分からない人だったら、これを目視で何度だと決めつけるのは難しいと思います。しかし、
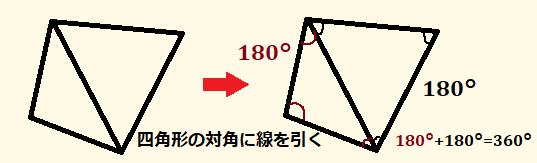
四角形に左図の通り線を引きます。すると、三角形が2つくっついた形になることが分かります。三角形の内角の和は180°ですから、それが2つあるので、
180°+180°=360°
となります。ただ2つの三角形の内角の和を足し合わせただけで分かるのか?と思うかもしれませんが、
右図の方でしっかり四角形の4つの角が三角形を構成する角になっていることが分かると思います。
同じように、他の多角形でも線を引いて、内角の和を知ることが出来ます。
さて、四角形から八角形までの内角の和を求めてみましょう!


内角の和には規則性がある!
| 角の数 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 内角の和 | 180° | 360° | 540° | 720° | 900° | 1080° | … |
さて、みなさん、求めることが出来たでしょうか?
上の表がその結果です。三角形が180°、四角形が360°、五角形が540°…のように角が多いほど内角の和が増加していることが分かると思います。何故かというと、角が増えるとその分引く線が増えて、多角形の中の三角形の数が増えていくからです。
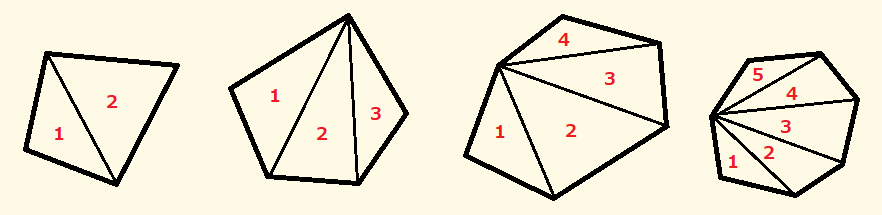
上の図は左から順に4,5,6,7角形になっていますが、三角形の数は2,3,4,5となっています。これを簡単に式で表すと、
角の数-2=三角形の数
という風にいうことが出来ます。
これらの規則性を踏まえて、もう少し深く考えてみましょう。
| 角の数 | 3 | 4 | 5 | 6 | 7 | n |
| 内角の和 | 180°×(3-2) | 180°×(4-2) | 180°×(5-2) | 180°×(6-2) | 180°×(7-2) | 180°×(n-2) |
上の表で数字を赤くした部分が角の数と対応していて、それをすべての場合で-2しています。
これが上で求めた表の値と合致します。
これを他の角に対しても用いることが出来るように式で表すと、
n角形の内角の和=180°×(n-2)
となります。これで、いくら角が大きな多角形であっても、その内角の和を知ることが出来ます!
外角の和の求め方を考える
さて、外角の和はどうでしょうか。五角形を例にとって考えてみましょう。
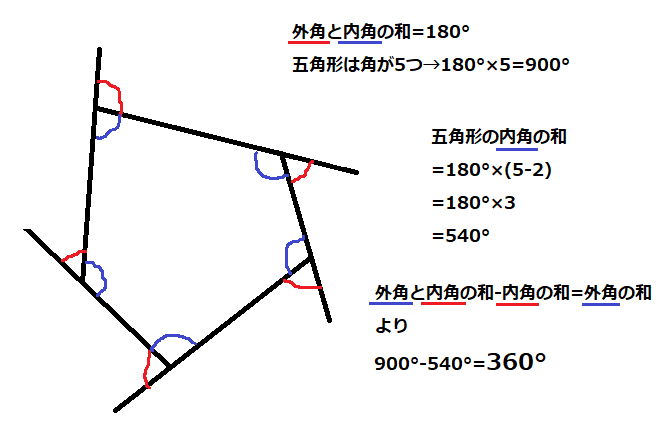
外角の和を直接求めることは出来ませんが、外角と内角の和が180°ということは分かっていますね。五角形の場合はそれが5つあるので、五角形の外角と内角の和が900°であることが分かっています。
一方で、内角の和は先ほど求めたように、180°×3=540°ですね。
さて、外角と内角の和から内角の和を引くと、残るのは外角の和のみになるので、
900°-540°=360°
となります。
さて、他の多角形についても考えてみましょう!


多角形の外角の和は360°!
| 角の数 | 3 | 4 | 5 | 6 |
| 内角と外角の和 | 180°×3=540° | 180°×4=720° | 180°×5=900° | 180°×6=1080° |
| 内角の和 | 180° | 360° | 540° | 720° |
| 外角の和 | 540°-180°=360° | 720°-360°=360° | 900°-540°=360° | 1080°-720°=360° |
計算結果が上の表です!どれも外角の和が360°となっています。
従って、外角の和は角の数によらず360°です!
まとめ
- 内角と外角の和は180°となる
- n角形の内角の和は180°×(n-2)となる。
- n角形の外角の和は360°となる。
やってみよう!
20角形の内角の和を求めよう。
こたえ
180°×(20-2)=180°×18=3240°
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
”やる気”と”自信”を育てる、あすなろ関西の学習サポート
どんな単元もコツをつかめば驚くほどスムーズに理解できるようになります! だからこそ、一人で悩み続ける必要はありません。
あすなろ関西は、「やる気づくり」や「できる喜び」を一番に考え、得意な教科から指導することで自信を持ってもらうことを重視しています。
まずはその第一歩として、自宅でもオンラインでも受けられる無料体験授業を、ぜひお気軽にお試しください!