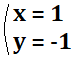こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、数の集合という考え方と、その集合の中で計算できる計算ってどんなことか、という2点について、なるべく分かりやすく解説していきます!
概念の話は少し分かりにくいかもしれませんが、こういった話を理解すると、この先数学の内容が複雑になっていってもその理解を楽にするのに役立ちます!
では、今回も頑張って読み進めてみて下さいね!
負の数を含む四則計算について勉強したい方はこちら!
加法(足し算)→【中1数学】負の数の足し算のやり方が分からない人必見!数直線を使った簡単な計算方法を解説!
減法(引き算)→【中1数学】負の数の引き算が分からない方必見!数直線を用いた考え方を解説します!
乗法(掛け算)→【中1数学】負の数を含む掛け算が分からない方必見!考え方と計算方法を解説!
除法(割り算)→【中1数学】負の数を含む割り算が分からない方必見!考え方・計算の仕方を解説します!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校1年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
数の集合
集合って言葉、数学では聞きなれないですよね。普段の生活で使う意味としては、「集まったり、集めたりする」ですね。
これは数学ではどういう意味で使われるかというと、「ある条件をみたすものをすべて集めたもの」となります。集めるものは数字で、条件は様々あります。ここで重要なのは「すべて」集めるので、一度決めた条件に対して満たすものはすべてそこに含まれるし、少しでも満たさなければ含まれません。
このような条件を決めて集合を考えることで、バラバラな数字の規則性や特徴が見えてきます。
さて、小学校で扱ってきた数字は、\(1,2,3\)といった数であったり、\(0.1\)や\(\frac{1}{10}\)といった小数・分数がありました。そして、中学数学に入ってから、\(-1,-2,-3\)という「負の数」が登場して、取り扱う数の範囲は格段に増えました。
これらの数の範囲の特徴を捉える為に、広い範囲の集合から狭い範囲の集合までを考えていきたいと思います。
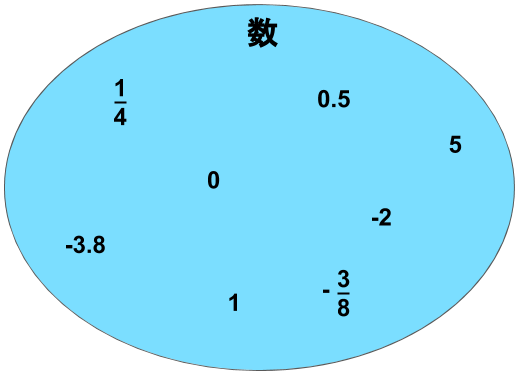
数
まず、「数」という集合を考えていきます。これは、正の数・負の数に関わらず、今まで扱ってきた数字すべてが含まれるとします。
まだ分類していませんが、図にするとこのような形で表されます。
整数
次に、整数という集合があります。これは、数の中でも\(-3\)や\(0\)や\(6\)など、小数点が付かない数や、分数の形でない数がこれに当てはまります。これも正の数・負の数の両方が含まれます。
そして、整数は数全体の一部です。(数を「日本」とすると、整数は「大阪府」、という感じのイメージです。大阪府は日本の一部です。)
これを図に表してみると、
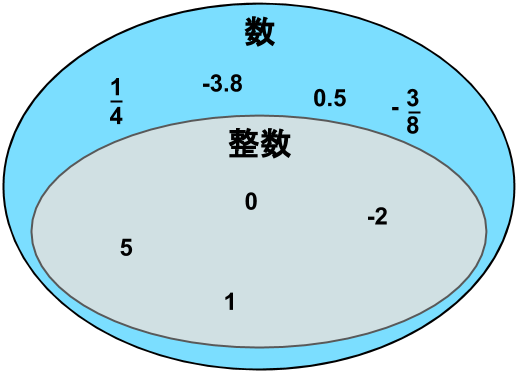
このようになります。集合を示すときに、ある一つの集合が、他の集合に完全に含まれているときは、大きい集合が小さい集合を囲むように示します。
自然数
「整数」という集合の中に、さらに「自然数」という小さな集合をつくることができます。自然数はこの単元で新しく登場した「個数や順番を表す数」を示す用語でした。従って、どのような値が含まれるかというと、「\(1\)、\(2\)、\(3\)…」と続く数です。1こ、2こや3番目、4番目と数えられる数なので、負の数や\(0\)は含まれません。
そして、自然数は整数の一部でもあります。(整数を「大阪府」とすると、自然数は「大阪市」というイメージです。すると、大阪市は大阪府の一部であり、日本の一部である、という風に考えられます。)
これらを図に表すと、このように表されることになります。
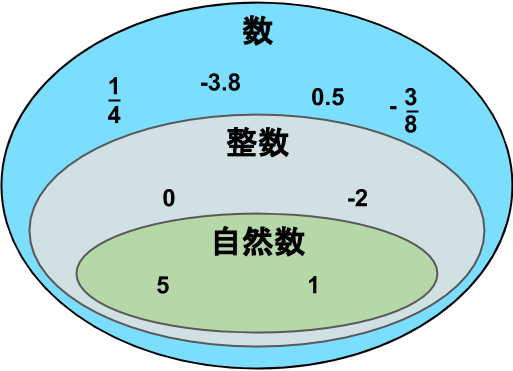
ところで、小数や分数は整数や自然数には含まれませんが、「数」全体の集合にはあると考えられますね。
四則計算での数の範囲
数を大きい集合から小さい集合まで見ていきましたが、それぞれの集合の範囲内で計算できるのは(すなわち、\(〇+△=□\)という式があった時、\(〇\)と\(△\)と\(□\)が同じ集合に属する数である計算が常にできるのは)、四則計算のうちどの計算となるのかを考えてみましょう。(\(〇÷0\)は除いて考えることとします。)
数の場合
数全体の場合、いうまでもなく「加法・減法・乗法・除法」のすべてが範囲内で計算できます。
例.
- \(0.3+4=4.3\)
- \(\frac{1}{4}×(-4)=-1\)
- \(\frac{4}{3}-1=\frac{1}{3}\)
- \(4÷8=\frac{1}{2}\)
整数の場合
整数の範囲ではどの計算が出来て、どの計算が出来ないのか調べてみましょう。式の値に適当な整数を入れ、その答えがどんな場合でも整数になれば、整数の範囲のみの計算が出来るということが確認できます。
加法では…
- \(3+(-4)=-1\)
- \((-3)+(-9)=-12\)
- \(4+7=11\)
整数のみの数で作った加法の式の答えはどれも整数になりました。従って、加法は整数の範囲で完結する計算が出来る、ということになります!
「他にもあるんじゃないの?」と思う人は、是非好きな整数を入れて計算してみて下さい。
減法では…
- \(3-(-4)=7\)
- \((-3)-(-9)=6\)
- \(4-7=-3\)
整数のみの数で作った減法の式の答えはどれも整数になりました。従って、減法は整数の範囲で完結する計算が出来る、ということになります!
乗法では…
- \(3×(-4)=-12\)
- \((-3)×(-9)=27\)
- \(4×7=28\)
整数のみの数で作った乗法の式の答えはどれも整数になりました。従って、乗法は整数の範囲で完結する計算が出来る、ということになります!
除法では…
- \(3÷(-4)=-\frac{3}{4}\)
- \((-3)÷(-9)=\frac{1}{3}\)
- \(4÷7=\frac{4}{7}\)
整数のみの数で作った除法の式は、整数ではない答えが出てきました。ということは、除法は必ずしも整数の範囲で完結する計算が出来るわけではない、ということになります。
例では全て分数の答えとなりましたが、整数の商となる場合も当然あります。しかし、加法・減法・乗法とは違い、整数同士の計算であっても、商の答えの範囲は「数全体」となるということを覚えておきましょう。
自然数の場合
自然数の範囲に絞ると、どの計算が出来ないのか調べてみましょう。
ちなみに、除法は整数の時点で答えが「数全体」になることが判明しているので、自然数での計算であっても、その商は自然数に収まりません。従って、残り3つの計算則について考えてみましょう。
加法では…
- \(5+2=7\)
- \(3+6=9\)
例が少ないですが、自然数のみの数で作った加法の式の答えはいずれも自然数になりました。従って、加法は自然数の範囲で完結する計算が出来る、ということになります!
小学校でやってきた計算ですし、足し算が自然数以外の整数(0や負の数)の答えにならないことは想像がつくと思います。
減法では…
- \(5-2=3\)
- \(3-6=-3\)
自然数のみの数で作った減法の式の答えは、負の数もあり得るということが分かりました。負の数は自然数ではないので、減法については、その答えの範囲は「整数」となります。
従って、加法は自然数の範囲で完結する計算が出来るとは限りません。
乗法では…
- \(5×2=10\)
- \(3×6=18\)
自然数のみの数で作った乗法の式の答えはいずれも自然数になりました。従って、乗法は自然数の範囲で完結する計算が出来る、ということになります!こちらも2つしか例を挙げませんでしたが、どんな自然数だったとしても、その積は自然数になることは想像がつくと思います。
数の範囲と四則計算の関係の図
ここまで確認してきたことを図にすると、このようになります。
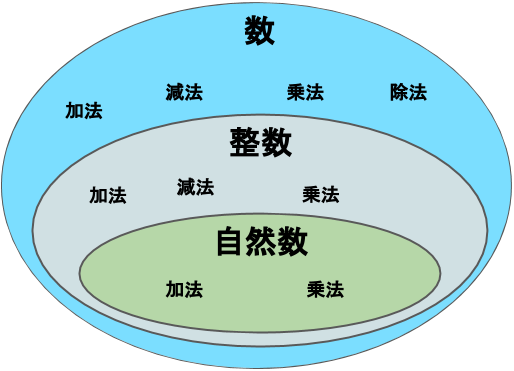
小学校の算数で主に扱ってきた自然数では、実は加法と乗法しかまともに計算できませんでした。(割り算や引き算は私たちが自由に決めた数字では、外の範囲にはみ出してしまうので、使えなかったのです。)しかし、整数の集合や数全体の集合に拡張することによって、減法や除法を制限なく、いつでも求めることができるようになります。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。