こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、円周角の定理の逆について解説していきます。
円周角の定理について分かっていれば、そこまで難しいことはありませんが、
学校や教科書の説明では少し難しく感じる部分があると思う部分であると思うので、
分かりにくい部分を噛み砕きながら説明していきます!
円周角の定理について分からない方でも読み進められるように、本編の前に解説していますので、良かったら最後まで読んでみてください。
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。 この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
【復習】円周角の定理とは?
円周角の定理とは、円の円周角と弧、中心角の関係について示した定理となります。
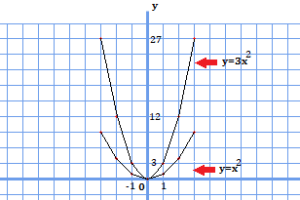
その1:同じ弧に対する円周角の大きさは等しい
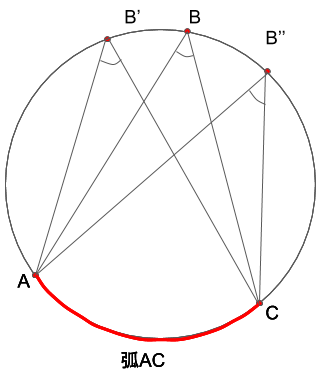
上の図では、弧ACに対する円周角である∠ABC,∠AB’C,∠AB’’Cを示しています。証明は省きますが、この図の様子から分かる通り、同じ弧に対してできる円周角はどれも同じ大きさとなっていることが分かります。
その2:同じ弧に対する円周角の大きさは、中心角の半分である
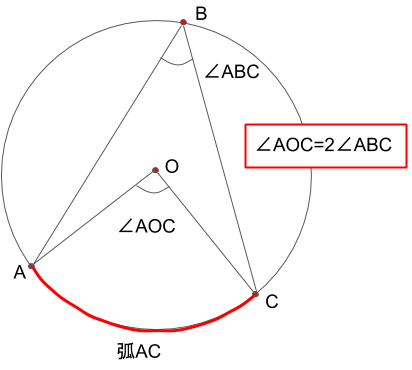
弧に対する円周角の大きさは、中心角の半分となります。なぜこのようになるのかという証明についてはこちらで説明していますので、気になる方は確認してみてください。
円とは何か考えてみよう
円とはどのように定義されているのか(円を円であると決めているのか)を考えたことがあるでしょうか。
今回はこれについて改めて考えつつ、「円周角の定理の逆」の意味について考えていきたいと思います!
距離による定義
円というのは、ある点からの距離が等しい点を集めたもの、と考えることが出来ます。
多くの方はコンパスを用いて円を引いたことがあると思いますが、なぜあれで円が引けるかというと、この性質を利用しているからです。ほとんどの場合、このある点を中心Oとして、この中心Oから円周までの距離を半径と言っていますね。
角度による定義はできる?
円は角度を使って定義することもできるかもしれません。
その理由は、円周角の定理による考え方によるもので、「1つの円の同じ弧に対する円周角の大きさは等しい」ということを利用すれば、その逆である「同じ弧(ある2点)に対して円周角の大きさが等しい場合、それは円だ」ということも出来るのではないか?ということです。
円周角の定理の逆
さて、円周角の定理の逆が正しいことを決定づけるためには、
「とある2点に対して同じ角度をとる2つの点があったとき、その点は同じ円周上にある」
ということを証明できればいいのです。
さて、円周上の点A点Bと、その2点によってできる円周角∠ACBとなる点Cをきめたとき、もう一つの角を作る点Pの位置による∠APBとの大きさを比較してみましょう。
ここで、分かりやすくするために、∠ACB=∠cと表すことにします。
点Pが円の外側にある場合
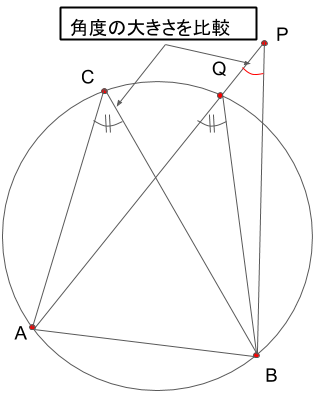
点Pが円の外側にある場合、次の図のようになります。
∠cと∠APBを比較すると、見た感じからして、∠APBは小さく見えます。
なぜ小さくなるのかを考えてみましょう。
APと円周の交点をQとしたときに、∠AQBは△QBPの外角となっていることが分かります。
外角の大きさはその点を使わない残り2つの角の大きさの和だったので、式で表すと、
∠AQB=∠APB+∠PBQ
となりますね。ここで、∠AQBは円周角の定理より
∠AQB=∠ACB=∠c
であるので、これを代入すると、
∠c=∠APB+∠PBQ
となります。さて、今調べたいのは、∠APBと∠cがどちらの方が大きいかということでした。右辺の方に∠PBQが入っているので、これを除いた関係式にすると、
∠c>∠PBQ
となります。
このように、証明からも、確かに円周の外側の点Pによる角は、円周上の角に比べて小さくなることが分かります。
点Pが円周上にある場合
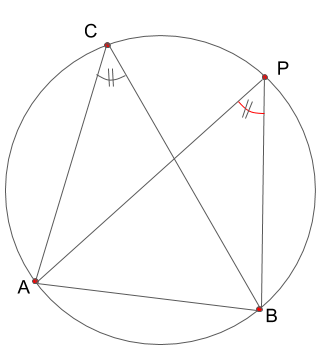
点Pが円周上にある場合は、円周角の定理により、∠cと等しくなります。
点Pが円周の内側にある場合
点Pが円周の内側にある場合、次の図のようになります。
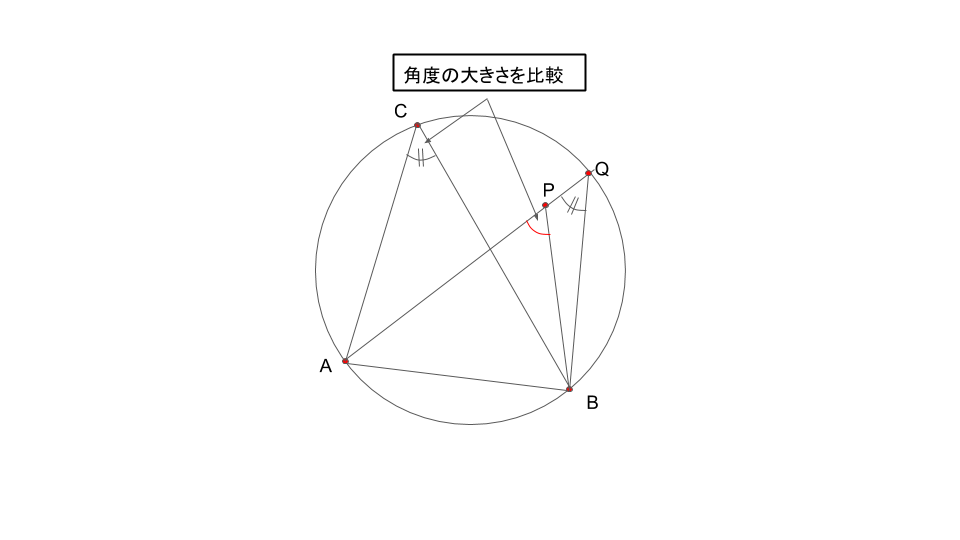
∠cと∠APBを比較すると、見た感じからして、∠APBは大きく見えます。
円周の外側のときと同様に、∠cと∠APBの比較をしてみましょう。
APをP側を延長して、円周と交差する点をQとすると、
∠APBは△PBQの外角となっていることより、
∠APB=∠AQB+∠QBP
となります。ここで、∠AQBは円周角の定理より、
∠AQB=∠ACB=∠c
となります。これを代入すると、
∠APB=∠c+∠QBP
であるので、
∠APB>∠c
となります。これより、円周の内側の点による角は、円周上の点による角に比べて大きくなることが分かりました。
この3つについて考えると、
- 円周より外側の点による角は、円周上の点の角より小さい
- 円周上にある点による角は、円周上の別の点の角に等しい
- 円周より内側の点による角は、円周上の点に角より大きい
となります。これより、∠cすなわち∠ACB=∠APBとなるとき、
それらの4つの点は円周上にあります。
円周角の定理の逆
4点ABPQについて、PQが直線ABで分けられる空間の同じ側にあり、
∠APB=∠AQB
であるならば、この4点は1つの円周上にある。
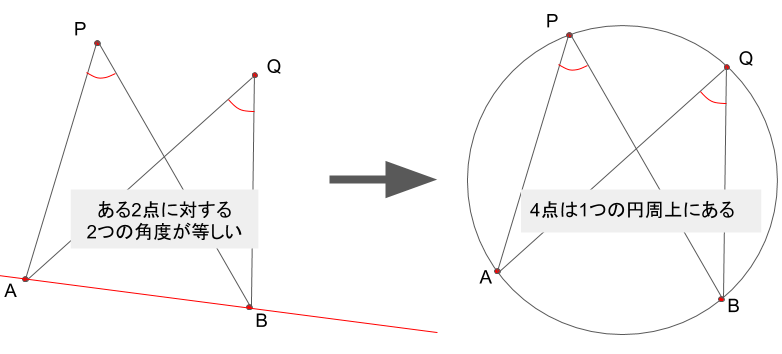
さて、AQとBPの交点をRとすると、それ以外の角は、
∠PAQ=PBQ
∠PRA=∠QRB
となっており、△ARPと△BRQは合同であるということが分かります。
この関係も証明等で使われることがあるので、良かったら覚えてみて下さい。
まとめ
円は3点を決めると、それを通る1つの円に決めることが出来ます。そして、それらの点が完全に重なっているということがない限りは、どこに点があっても円を作ることが出来ます。
ところが、4点以上の任意の点(テキトウに置いた点)をすべて通る円というのは、存在する場合と存在しない場合があります。
そのうち、この「円周角の定理の逆」を理解することで、ある4点以上の点がすべて同一の円周上にある円であるかどうかを確かめることが出来る手段なのです。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。