数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がった途端分からなくなってしまう人が多いです。今回は高校1年生の数学の中でも方程式・不等式について書いていきたいと思います。この単元は数学はもちろん、物理などでも使うのでしっかりと押さえておかないと後から困ってしまいますよ。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
不等式
不等式とは大小関係を表した式です。中学の時にも不等式は登場しましたが、高校の数学Ⅰのこの単元では、与えられた不等式の条件を満たすxの範囲を求めていきます。このxの範囲を求めることを「不等式を解く」といいます。
不等式の性質
不等式を解くためには方程式のように式変形をする必要があります。式変形の根拠をしっかりと説明するために不等式の性質をしっかりと理解する必要がありますね。不等式の基本的な性質をまずはしっかりとおさえましょう。
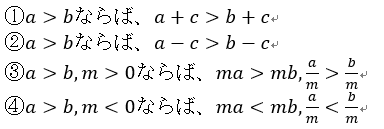
上の性質からも分かるように、不等式では方程式と同じように移項することができます。方程式と違って気を付けなければならないことは、両辺に負の数をかけたり割ったりするときに不等号の向きが変わることです。
絶対値を含む不等式
絶対値とはゼロからの距離です。絶対値が2の数は、+2と-2です。なので、方程式|x|=2の解はx=±2ということです。
では不等式に絶対値が含まれている場合を考えてみましょう。絶対値が2よりも小さい数は-2よりも大きく+2よりも小さい実数です。なので、不等式|x|<2の解は-2<x<2ということです。
次に不等号の符号を逆向きにして考えてみましょう。絶対値が2よりも大きい数は-2よりも小さい数と+2よりも大きい実数です。なので、不等式|x|>2の解はx<-2,x>2ということです。
連立不等式
方程式で連立方程式があったように、不等式でも連立不等式があります。連立方程式と同じようにいくつかの不等式が組み合わさっていて、それらの不等式を同時に満たすxの範囲を求めることを連立不等式を解くといいます。
よくある例題
不等式の例題をいくつか紹介していきます。
例題 (計算問題)
\(x+10>4x-8\)を解け。
解答
\(x+10>4x-8\)
\(18>3x\)
\(x<6\)
移項して計算するだけです。
例題 (連立不等式)
連立不等式\(\begin{eqnarray} \begin{cases} 7x – 12 > 10x -9 & \\ 4x + 3 > 2x – 5 & \end{cases} \end{eqnarray}\)を解け。
解答
それぞれの不等式を解いて、共通の範囲が解となります。
それぞれの不等式を解くと
\(7x-12>10x-9\)
\(3x<-3\)
\(x<-1\) ・・・①
\(4x+3>2x-5\)
\(2x>-8\)
\(x>-4\)・・・②
①と②の共通範囲を考えて、
\(-4<x<-1\)
となります。
例題 (絶対値を含む)
\(|2x-5|<3,|2x-1|>9\)を解け。
解答
\(|2x-5|<3\)より、
\(-3<2x-5<3\)
\(2<2x<8\)
\(1<x<4\)
\(|2x-1|>9\)より、
\(2x-1>9\)または\(-(2x-1)<9\)
それぞれの不等式を解くと
\(x<-4,x>5\)
苦手克服法
よくある悩み
不等式の計算が苦手だという人は、連立不等式や絶対値を含む複雑な不等式が出てくると途中で分からなくなってしまう、という人が多いでしょう。頭の中で考えながら、式を書いて計算していると、途中で「ん?」と思うことはあると思います。
そんなあなたは
不等式の計算が苦手な人は、数直線などの図を書くようにしましょう。図を書いていれば後から見直すときも分かりやすく、整理しやすいです。また、絶対値を含む不等式の計算が苦手だという人は手順を踏んで不等式を解いていくようにしましょう。まず、場合分けをして絶対値記号をはずし、普通に不等式を解き、場合分けの条件を満たしているか確認し、解をまとめる。このような手順で解いていくようにしましょう。
不等式を解く時に気を付けること
不等式を解く時に一番気を付けなければいけないことは、負の数をかけたり割ったりする時です。また、絶対値記号をはずして計算した後は、はじめにはずした時の条件を満たしているか確認しましょう。分かっていても忘れてしまうことがあるので毎回確認するクセを付けましょう。それに加えて、複雑な問題の時は数直線を使って、目で見てすぐわかるようにするといいですね。