こんにちは、あすなろスタッフのカワイです。
今回は、反比例の式や性質について、具体例から解説していこうと思います。比例は数が増えると一定数増えたり減ったりするなど、分かりやすい部分が多かったですが、反比例は少しそれとは異なるアプローチとなるので、取っ掛かりにくいかもしれません。なるべく分かり易く解説していくので、頑張ってついてきてください!では今回も頑張っていきましょう!
関連記事:【中1数学】比例のグラフの書き方とそのグラフの特徴について知ろう!(その2)
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
反比例の考え方とは?
図形の面積と辺の長さの関係を例に説明していきたいと思います。
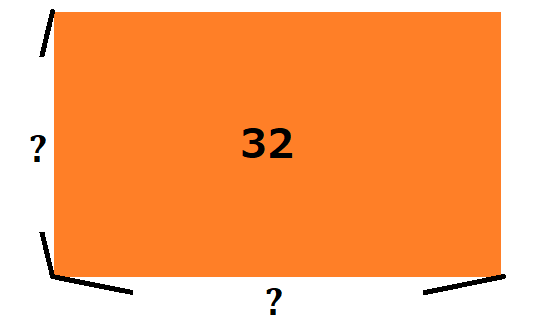
面積が32の長方形がありますが、辺の長さはどちらも分かりません。したがって、
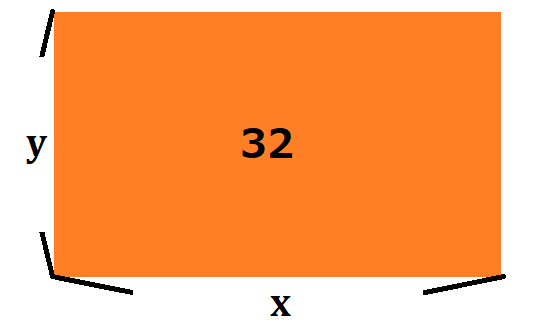
たてを\(y\)、よこを\(x\)とおいてみます。
どちらか一方が定まると、面積が32となるように、もう一方も決まります。
ということは、これは関数として式で示すことが出来そうです。
面積=たて×よこ で求めることが出来るので、これを元に表を作ってみましょう。
値を表に表してみる
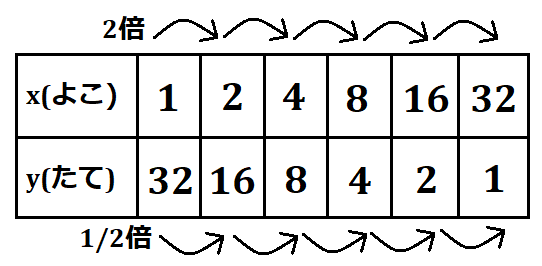
\(x\)(よこ)が\(2\)倍長くなると、\(y\)(たて)が\(\frac{1}{2}\)倍になります。増えるほどもう一方が減っていくというのは比例定数が負の場合も同様でしたが、比例の場合は\(x\)と\(y\)どちらも同じ倍数だけ変化していっていましたね。ここが大きく異なるポイントです!
一方、このよこと縦をかけると、どれも32となっています。(面積は変わらないという前提なので当然ですね)
このように、ある決まった値の範囲内で、掛け算の2つの項の組み合わせを見つけることができます。
式で表現してみる
面積=たて×よこ
で表すことが出来ると説明しましたので、実際に式で表現してみると、
$$32=x×y$$
$$32=xy$$
と表すことが出来ます。これを\(y\)の式に書き換えると、
$$y=\frac{32}{x}$$
となります。
反比例の公式
\(32\)の部分を\(a\)とおくと、
$$\frac{a}{x}$$
となります。これが反比例の公式となります。\(a\)の部分は比例の公式と同様に比例定数といいます。
反比例での比例定数\(a\)は、今回の面積と同様に、掛け算の積になる部分が比例定数となっています。(比例では、掛け算の項となる部分が比例定数となっています)
反比例をグラフに表してみよう
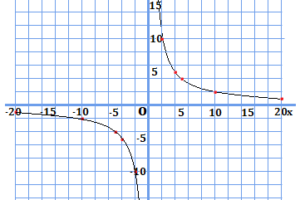
表にいくつかの値をとったので、これを元にグラフを作成してみましょう。
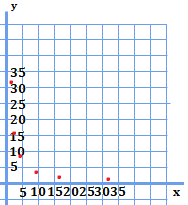
比例のグラフは直線であったのに対し、反比例では、単純に結ぶことができなさそうな位置に点が並びました。これらは曲線で結ぶことが出来るのですが、これを双曲線といいます。
実際に結んでみるとこうなります。

そういえば、比例のグラフでは原点を必ず通りましたが、反比例では\(x\)や\(y\)が0を通るでしょうか?
答えは、通りません。
式を見てもらえば一目瞭然ですが、
\(y=\frac{a}{x}\)は\(xy=a\)と書き換えることができ、\(x\)か\(y\)のどちらかに0がはいると、\(a\)も0にならなければ成立しません。aが0であればそもそも関数として成立しませんから、\(x\)や\(y\)が0となることはないのです。(面積が0になる辺の長さはなにか?と言われても困りますよね)
まとめ
反比例の公式
\(y=\frac{a}{x}\) (ただし、比例定数は\(a\))
反比例の性質
- 一方の変数が2,3倍になると、もう一方の変数は1/2,1/3倍になる
- グラフで表現すると、曲線の形になる → 双曲線
- \(x\)や\(y\)が0になることはない
いかがでしたか?今回は反比例の勉強の入門編を行いました。比例と反比例という、似た名前でありながら、性質が全く異なるものだということを分かってもらえたらOKです。次回からは、反比例の性質にさらに踏み込んで、面白いところを紹介します!
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。