こんにちは、あすなろスタッフのカワイです。
前回はグラフの書き方を解説していきました。比例のグラフについての主な特徴について説明していきましたが、今回は前回と少し違う向きのグラフと、逆にグラフから式を読み取る方法について解説していきたいと思います。まだ比例のグラフの理解が不安な方は、前回の記事に戻って復習してから読み進めてみて下さいね!
では、今回も頑張っていきましょう!!
関連記事:【中1数学】比例のグラフの書き方とそのグラフの特徴について知ろう!(その1)
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
比例定数が負の場合のグラフ
例1.次の表をグラフに表してみよう。
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 6 | 4 | 2 | 0 | -2 | -4 | -6 | … |
今回は表からグラフに表してみましょう。
そのままグラフに点を入れていっても解けますが、この表がどのような規則性をもっているのか調べてみましょう。(これが比例関係であるとは限りません)
表からまず分かることですが、\(x=0\)になったときに\(y=0\)となっています。
また、値がどこを切り取っても\(x\)の値が1増えると、\(y\)の値が2減っています。従って、この関数は\(x\)に入れられた値を-2倍して\(y\)として出す関数であると考えることができます。
これを式に表してみると、
$$y=-2x$$
となります。この式の形は\(y=ax\)の形になっているので、この表で表された関数は、比例定数が\(-2\)の比例の関数であるとわかります。
今までは比例定数が正の数の場合で考えてきましたが、今回は負となっています。では、負の場合どのようなグラフとなるでしょうか?
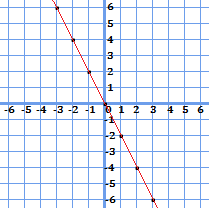
各点をグラフ上に置き、線を引いた結果、こうなりました。比例のグラフなので、原点を通る一直線となっています。
比例定数が正の数のグラフとの違いは何かと考えると、傾きの向きが異なります。
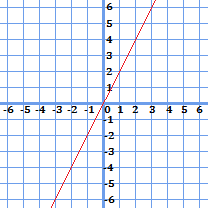
上に示したのは\(y=2x\)のグラフです。これを見ると、比例定数が
負の場合:左上~原点~右下
の場所に値をとります。傾きの大きさについては、比例定数の絶対値(今回の場合-2と2)が同じであれば、向きは異なりますが、大きさ自体は同じです。
グラフから式を取り出す方法
今度は、ある比例関数のグラフから式を導出する方法について解説していきます。
繰り返しになりますが、、比例のグラフってどういうものだったかというと、
- 原点を通る
- 取りうる値がすべて一直線上にある
という2つの特徴がありましたね。
したがって、これらの特徴を持つグラフであれば、\(y=ax\)の形に書くことができるはずです。
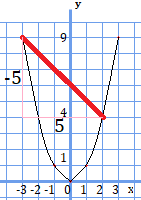
例2.このグラフを式で示してみよう
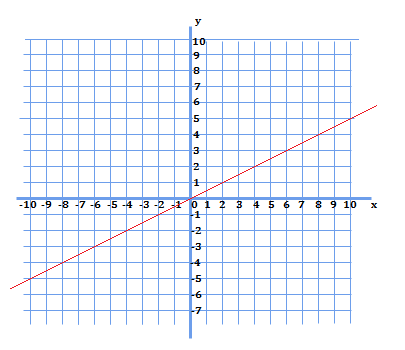
このグラフの求め方を知る前に、まずいくつか新しい説明をしなければなりません。まず、グラフ上の点のことを座標といいます。この言葉はグラフを用いる際によく出てくるので、覚えてください!
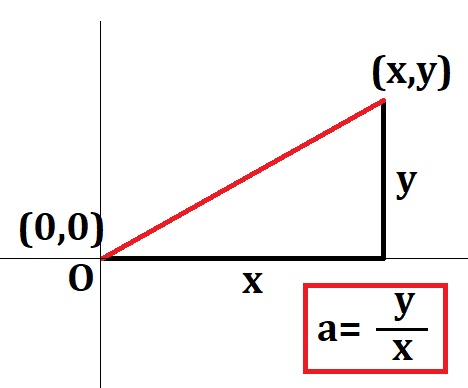
次に、このつたない上の図ですが、グラフだと思ってください。図を見てみると、(0,0)や(x,y)と表されたところがあります。グラフ上の値を示したい時にこのような形で表され、\(x\)がaで\(y\)がbの時、(a,b)と表します。グラフ以外でもよく用いられるので、こちらも覚えてくださいね。
では、赤い線の傾きを知りたい時、どうしたらよいか考えると、図の通り\(\frac{y}{x}\)をしてあげると求めることができます。(\(a=\frac{y}{x}\)は\(y=ax\)のグラフの形を変形しただけです!)

さて、グラフに戻りましょう。このグラフは、原点を通り、一直線となっているので、\(y=ax\)で表すことができると分かります。ここから比例定数\(a\)を読み取ることができれば、このグラフを式で表すことが可能です。
どの点からでも読み取る事は可能ですが、分かりやすい説明の為に、原点付近で考えてみましょう。線が交差している\(x=2\)、\(y=1\)の点を拡大してみました。
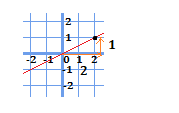
先ほどの考え方を用いて傾き(=比例定数\(a\))を計算すると、
$$a=\frac{1}{2}$$
となります。
従って、このグラフに示された式は
$$y=\frac{1}{2}x$$
となります。これが正しいか確かめたいときは、\(x\)に4や6などグラフ内にある値に対応する\(y\)を見てみればすぐに確認できます。
まとめ
- 比例定数が負 → 傾きの方向が左~右下へ
- 座標は(a,b)で表す
- 傾きは\(\frac{y}{x}\)で求める
傾きを求めることが出来れば、比例のグラフであればどのグラフでも式に表すことが出来ます!また、グラフの点から比例の式を表すこともできます。ここまでの内容で、比例は最低限理解できたといえるでしょう!
今回の内容の練習問題があるので、よかったら理解度を確認してみてください!
やってみよう
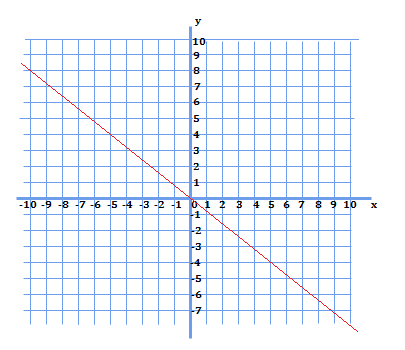
1.次のグラフから式を導出してみよう。
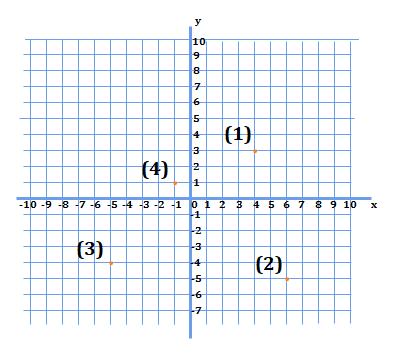
2.次のグラフ上の座標を示せ
こたえ
1.\(y=-\frac{4}{5}\)
2.(1) \((4,3)\)
2.(2) \((6,-5)\)
2.(3) \((5,-4)\)
2.(4) \((-1,1)\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。