こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、立体図形とは何か?そして、角柱や角錐について解説していきたいと思います。
そして、立体図形は平面図形の応用になります。平面図形が苦手な方は、一度復習してから読んでみて下さい!一層理解が深まると思います。
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。 この記事は数学の教科書の採択を参考に中学校1年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
立体図形とは
立体図形とは、平面図形の「縦」「横」に加えて、「高さ」という次元が増えた図形の事をいいます。
世の中に存在するものはほぼ全てが立体図形なので、平面図形よりも現実に近く考えやすいかもしれません。
立体図形の中で、全ての面が平面図形で出来た図形を多面体といいます。
例えば、
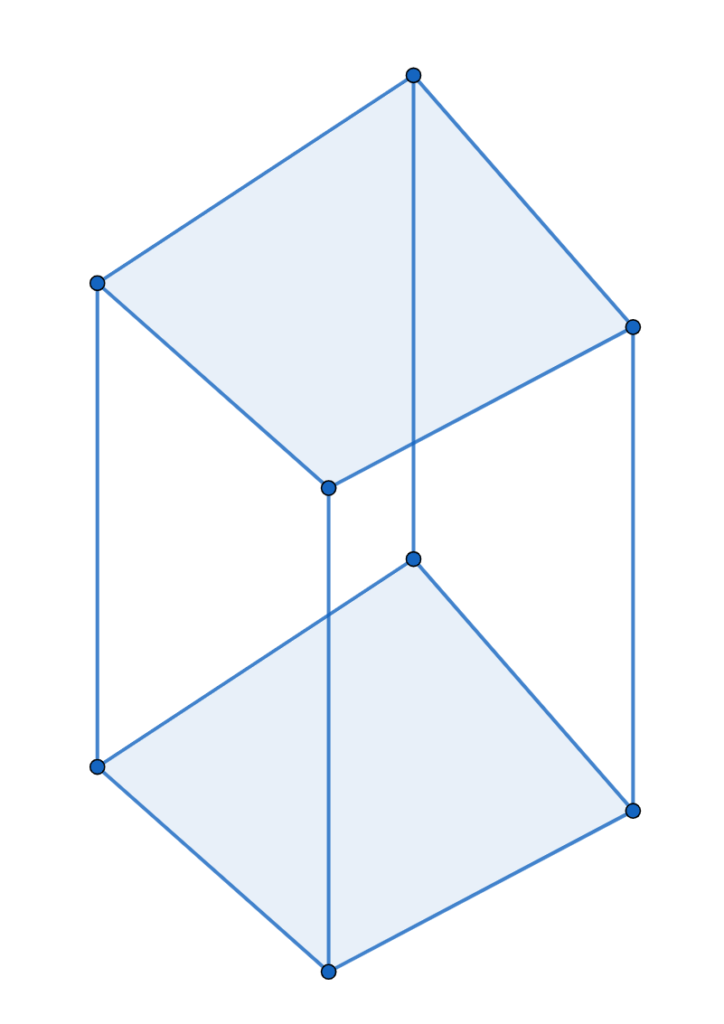
は、全ての面が四角形という平面図形で出来ているので、多面体となりますが、
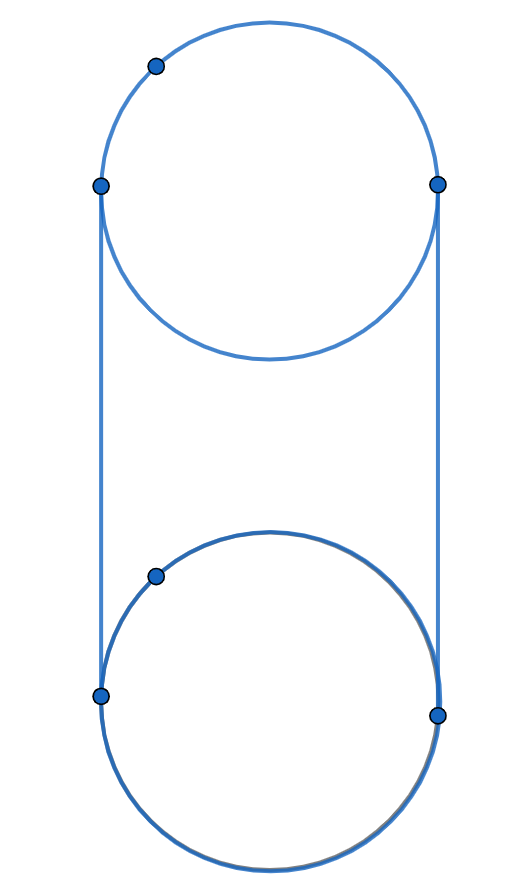
この図形は、上と下の円は確かに平面図形なのですが、そこを繋ぐ部分が平面図形ではないので、これは多面体ではありません。
さて、多面体の代表例として「角柱」と「角錐」の2つがあげられます。
今回は、その角柱と角錐の中でも、特によく登場する立体図形を紹介して解説していきます!
角柱
ある平面図形を、高さ方向に対して平行にそのまま厚さを増やしていくと出来る図形を角柱といいます。
早速、三角形をそのまま高さ方向に伸ばしてみると(厚さを増やしていくと)、どのようになるのか見てみましょう。
三角柱
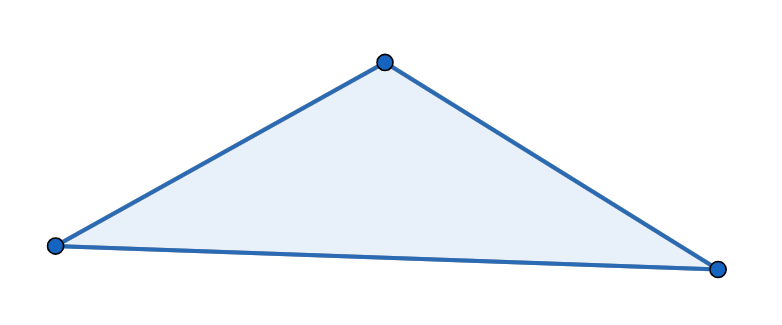
この何の変哲もない三角形を上に伸ばすと、
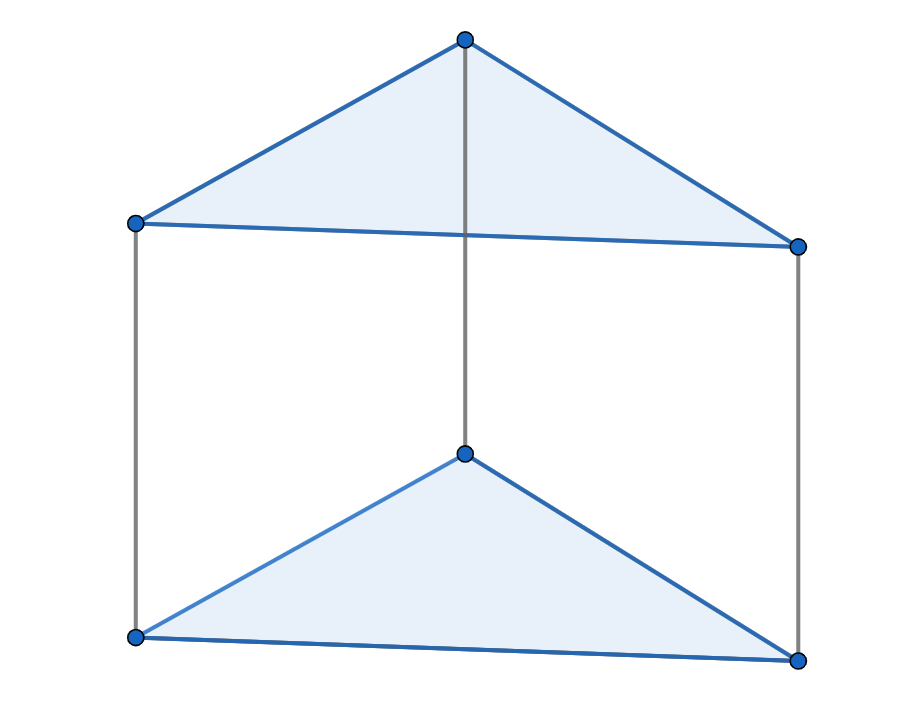
このようになりました。三角形をそのまま伸ばした図形なので、三角柱といいます。
特徴を見てみると、
- 三角の面が2つ
- 四角の面が3つ
- 辺の数が9つ
ということが分かります。(特徴は様々な図形を試した後に、最後にまとめていきますから、覚えなくて大丈夫です!)
さて、平面図形では「底辺」という言葉がありましたが、立体図形では、
「底面」
という言葉を用いてある平面自体を呼ぶことがあります。
例えば、今回の図形では、下側の三角形を底面と呼びます。
ここで紛らわしいのが、上側の三角形も底面と呼びます。上にあっても、底面です。
何故かというと、上下逆さにしても、概形(傍から見た形)は変わらないからです。
そして、それ以外の面を「側面」といいます。この図形の場合は、四角形の面3つが側面ですね。
四角柱
次に、四角形をそのまま高さ方向に伸ばしてみましょう。

この四角形を高さに伸ばしてみると、
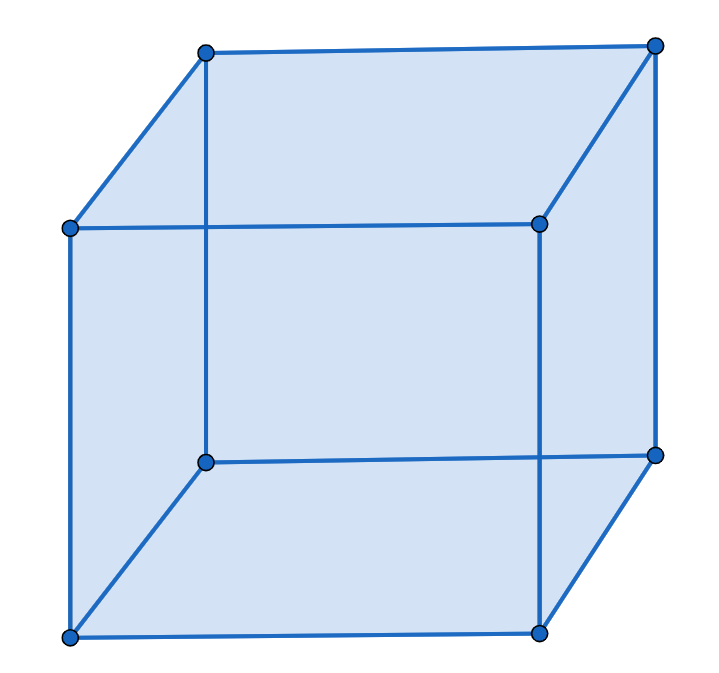
このようになります。四角形に伸ばした立体図形を四角柱といいます。
四角柱の特徴は、
- 面の数は6つ
- 辺の数は12つ
- 面の形はすべて四角形
であると分かります。
底面は三角柱と同様、上と下の四角形です。側面は底面と底面をつないでいる4つの四角形の面です。
角錐
角柱は平面図形をそのまま高さ方向に伸ばしたものでしたが、それに対して、平面図形から高さ方向のある1点に集まるようにできた立体図形を角錐といいます。
三角錐
三角形を1点に対して伸ばしていくと、どのようになるか見てみましょう。

このような何の変哲もない三角形を上に伸ばすと、
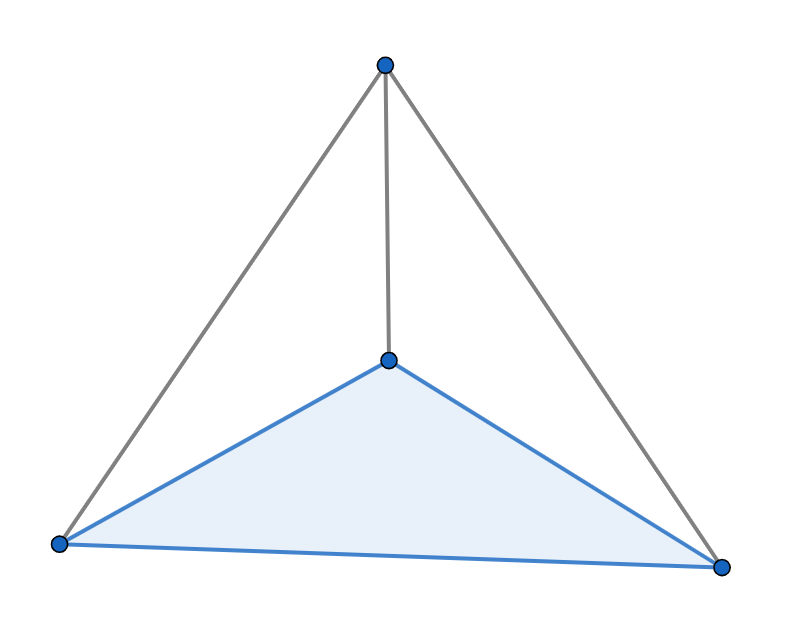
となります。これを、元々の平面図形(三角形)に因んで三角錐といいます。
この特徴を見てみると、
- 面の数は4つ
- 全ての面が三角形
- 辺の数は6つ
ということが分かりました。
底面は元にした平面である三角形で、側面は残りの3つの三角形となります。
底面に対して、面が集まってできた上部の点を頂点といいます。
四角錐
同様に、四角形を1点に対して伸ばしていきたいと思います。

これを高さ方向の1点に対して伸ばしていくと、
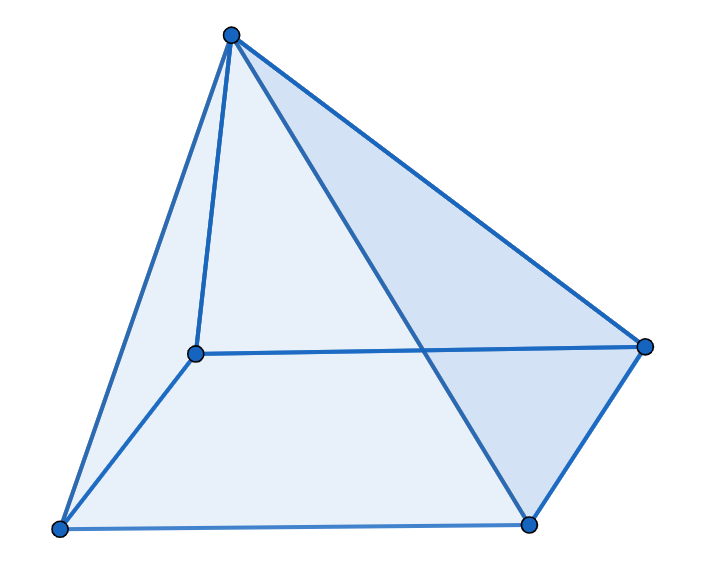
となります。これは四角錐といいます。
この特徴を見てみると、
- 面の数は5つ
- 1つの面が四角形、4つの面が三角形
- 辺の数は8つ
ということが分かりました。
底面は元にした平面である四角形で、側面は4つの三角形となります。
三角錐と同様に、上部の点を頂点といいます。
角柱と角錐の比較
ここで、角柱と角錐の比較をしてみましょう。
|
| 面の数 | 辺の数 | 底面の数 | 側面の数 |
| 三角柱 | 5 | 9 | 2 | 3 |
| 四角柱 | 6 | 12 | 2 | 4 |
| 三角錐 | 4 | 6 | 1 | 3 |
| 四角錐 | 5 | 8 | 1 | 4 |
ここから分かる通り、同じ平面図形が元である角柱と角錐の場合、角柱の方が角錐より底面が1つ多いことが分かります。
また、この表からは分かりませんが、角柱の場合は側面は全て長方形となります。
一方で、角錐の場合は側面が全て三角形となります。(二等辺三角形とはなりません。)
様々な角柱と角錐
さて、代表的な角柱と角錐を紹介してきましたが、○角形が無限に作れるように、○角柱や○角錐も無限に作ることが出来ます。見たことがない角柱や角錐であっても、見ただけで「これは○角柱!」「これは△角錐!」と瞬時に判断できるように、様々な角柱や角錐を見て判断できるようにしていきましょう!
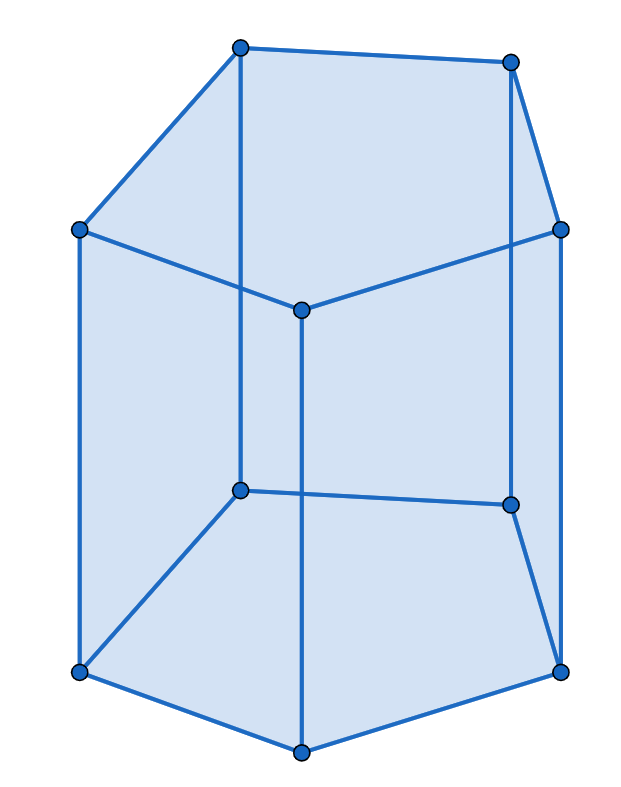
五角形と四角形の平面によってできた立体図形であると分かります。三角形がない時点で、角錐ではなく、角柱であると分かります。
また、五角形の面が2つあるので、これを底面とする図形だと分かります。
従って、これは五角柱です。
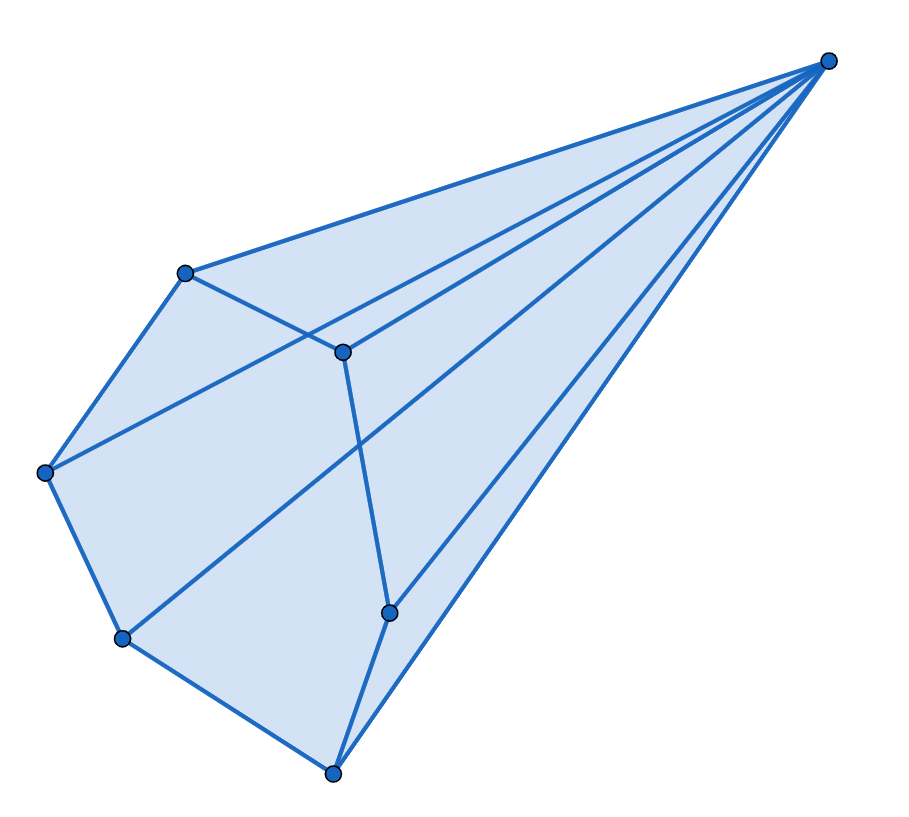
六角形と三角形の平面によってできた立体図形であると分かります。三角形があり、四角形がないので、角柱ではないと分かります。
また、六角形は1つで、残りはすべて三角形ということから、六角形を底面とする六角錐であると分かります。
まとめ
今回は角柱と角錐について解説しました!これらは見た目が結構違うので、ロジカルに考えなくても分かるかもしれません。それはそれでいいのですが、「この立体ってどんな特徴があるんだろう?」ということを考えながら問題と向き合うということも大切にして取り組んでみて下さい。
次回は、円を含む立体図形である「円錐」「円柱」「球」について解説していきますので、よろしければ読んでみて下さいね!
最後までご覧いただきありがとうございました。 「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報! 数学の単元のポイントや勉強のコツをご紹介しています。 ぜひ参考にして、テストの点数アップに役立ててみてくださいね。 もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。