数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。今回は高校1年生の数学の中でも三角比について書いていきたいと思います。三角比は数学はもちろん、物理などでも使うのでしっかりと押さえておきたいですよね。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
三角比の使い方
前回sin(サイン)、cos(コサイン)、tan(タンジェント)を紹介しましたが、これだけだと「だから何?」って感じだと思います。この三角比をを使ってどんなことができるか、を紹介していきたいと思います。
三角比の性質
三角比には、ある角度の時に決まった性質があります。
角度が「90°- θ」の時や、「90°+ θ」の時、「180°- θ」の時にθを使った三角比に変換することができます。
90°- θの時(0°≦θ≦90°)
sin(90°-θ)=cosθ
cos(90°-θ)=sinθ
tan(90°-θ)=-1/tanθ
90°+θの時(0°≦θ≦90°)
sin(90°+θ)=cosθ
cos(90°+θ)=-sinθ
tan(90°+θ)=-1/tanθ
180°- θの時
sin(180°-θ)=sinθ
cos(180°-θ)=-cosθ
tan(180°-θ)=-tanθ
必ず必要な公式
一通り三角比を使った計算をした後に出てくるのが正弦定理、余弦定理です。この2つは前に出てきた公式に比べて、少し複雑になってきます。しかし、この2つの公式を使えると求められるものが格段に増えます。
正弦定理
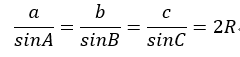
余弦定理
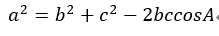
正弦定理に出てくるRは三角形の外接円の半径です。これらの公式は直角三角形だけでなく、すべての三角形で使える公式です。この2つの公式が使えるといろんな場面で角度、辺の長さが求められるので、頻繁に使うようになります。必ず使えるようになりましょう。
よくある例題
例題 (角度を変換する)
sin120°、cos135°を求めよ。また、sin154°、tan111°を90°未満の角度で表せ。
解答
上で出てきた式を使って変換すると、
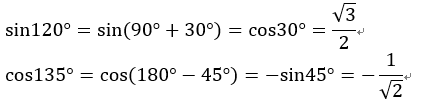
このように計算がしやすくなります。
また、キリのよくない角度でも、同じように変換できるので、
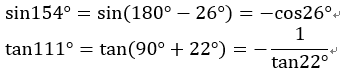
と変換できます。
例題 (正弦定理を使う)
△ABCにおいてBC=6、∠A=60°、∠B=75°のとき、ABの長さを求めよ。また、この三角形の外接円の半径を求めよ。
解答
正弦定理から、
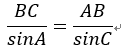
であるので、ABの長さを求めるためには、BC、∠A、∠Cが必要です。BC、∠Aは問題で与えられおり、∠Bが与えられているので∠Cも求めることができます。
∠C=180°- ∠A- ∠B=180°-60°-75°=45°
これでABを計算するために必要な値はそろったので正弦定理を使って求めていきます。
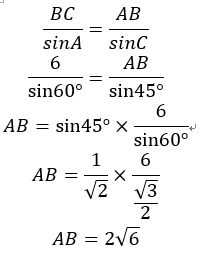
また、外接円の半径は、

このように辺の長さや外接円の半径を計算できます。
三角形の外接円の半径というワードが出てきたら正弦定理が使えるかもと考えられるといいですね。
例題 (余弦定理を使う)
△ABCにおいて、BC=1+√3、AC=2、∠C=60°のとき、ABの長さを求めよ。
解答
余弦定理から、
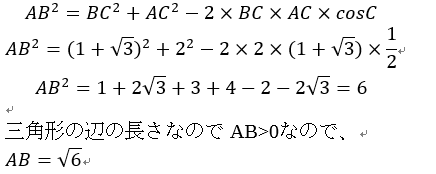
といった感じで計算できます。
また、余談ですがこのあとに正弦定理を使えば残りの角度も計算できます。
苦手克服法
よくある悩み
正弦定理や余弦定理は今まで出てきた公式よりも複雑になっていて覚えづらい、忘れてしまいそう、といった人もいるでしょう。また、「公式は覚えているけど問題が解けない」という人は「公式は覚えていて、公式に当てはめれば問題は解けるけど、どうしてこうなっているのがよくわからない」といった人は多いと思います。
解決策
公式を暗記したのに問題が解けない、授業ではわかったと思っていたのに問題が解けない、という人はしっかりと内容が理解できていません。授業では先生が最初から最後まで説明してくれるので、聞いているだけで分かった気になってしまいがちです。それに公式を暗記するのも確かに大事ですが、大切なのはその公式への理解です。その公式がどうして成り立つのか、という「なぜそうなるのか」を中心にして勉強をしてみましょう。
三角比攻略法
やるべきことは公式の中身を理解して、問題がきたらどの公式を使えばいいかわかるようにしておくことです。公式の理解に有効なのが公式の証明です。授業で公式を習う時にどのようにしてその公式が成り立つのかを一度は説明されると思います。公式の証明をしっかりと自分で説明できるようになれば、公式について理解がちゃんとできているでしょう。ここでも、理解することが大切なので、公式の証明を暗記してもあまり意味はありません。公式を自分の言葉で説明できるようになりましょう。































































