数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。今回は高校1年生の数学の中でも2次関数のなかの関数の最大最小について書いていきたいと思います。2次関数は苦手な人の多い分野なのでしっかりと押さえておきたいですよね。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
2次関数の最大最小
yがxの2次の多項式で表すことのできるとき、yはxの2次関数であるといいます。式で書くと、
\(y={ax}^2+bx+c\)
となります。
定義域とは
2次関数\(y={ax}^2+bx+c\)でいうと、xの取り得る範囲が定義域、yの取り得る範囲が値域です。また、定義域と値域を合わせて変域といいます。
xの定義域が全ての実数の場合
\(y={ax}^2+bx+c\)のグラフにおいて、2次の係数a が正である時、グラフは下に凸、係数a が負である時、グラフは上に凸になります。

そのため、xの定義域に指定が無い場合、2次関数の2次の係数aが正である時は図から頂点で最小値となり、最大値は無限大までいってしまうのでありません。2次の係数aが負である場合は図から頂点で最大値となり、最小値はマイナスの無限大までいってしまうのでありません。なので、定義域に指定が無い場合には、2次の係数の正負を確認し、頂点の座標を求めるだけで関数の最大最小を求めることができます。
xに定義域が限定された範囲の場合
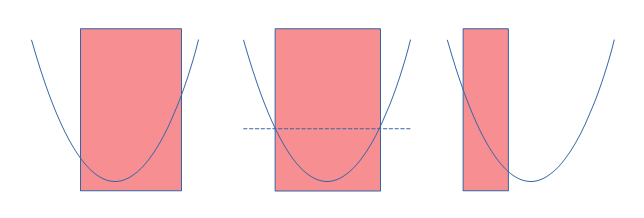
定義域に指定がある場合は、その範囲の中での最大値・最小値を考えなければいけません。例えば、下に凸のグラフを考えてみましょう。定義域に頂点が含まれている場合は、最小値は頂点の値になります。下の図で赤い部分を定義域とすると、左2つのグラフは定義域に頂点が含まれているので、最小値は頂点の値です。最大値は左の図の場合は定義域の右端が最大値です。しかし、真ん中の図では、定義域の右端と左端が同じ値なので、両方で最大値をとります。また、一番右の図のような定義域に頂点を含んでいない場合は定義域の端のどちらかが最大値でどちらかが最小値になります。
よくある例題
2次関数の最大最小についての例題をいくつか紹介していきます。
例題 (定義域のある2次関数の最大値と最小値)
関数\(y=x^2-2x+3(0≤x≤3)\)の最大値と最小値を求めよ。
解答
与えられた2次関数を平方完成すると、
\(y=x^2-2x+3\)
\(y={(x-1)}^2+2\)

よって、与えられたxの定義域でのグラフを描くと上の図のようになる。上の図から、頂点x=1の時に最小値2、x=3の時に最大値6を取る。
例題 (場合分けして求める)
関数\(y=-x^2+2ax(0≤x≤3)\)の最大値を①\(a<0\)➁\(0≤a≤3\)③\(3<a\)に場合分けして求めよ。
解答
与えられた2次関数を平方完成すると、
\(y=-x^2+2ax\)
\(y=-{(x-a)}^2+a^2\)
よって、このグラフは上に凸なグラフであり、aの値によって頂点が動きます。
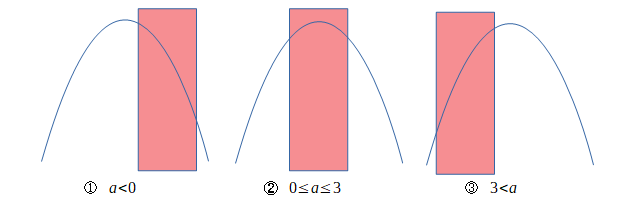
グラフを描くと上の図のようになり、赤色の部分が定義域です。なので図から、
①\(a<0\)の時
x=0の時に最大値0
➁\(0≤a≤3\)の時
x=aの時に最大値a^2
③\(3<a\)の時
x=3の時に最大値6a-9
例題 (2次関数を文字で置く問題)
関数\(y=-{(x^2-2x+2)}^2+6(x^2-2x+2)+1\)について、
①\(x^2-2x+2=t\)とおくとき、\(t\)のとり得る値の範囲を求めよ。
➁\(y\)の最大値を求めよ。
解答
①与えられた\(t\)の式を平方完成すると
\(t=x^2-2x+2\)
\(t={(x-1)}^2+1\)
よって、\(t\)の最小値は1、最大値は存在しないので、\(t\)のとり得る範囲は\(t≥1\)
➁与えられた関数をtを使って表すと、
\(y=-{(x^2-2x+2)}^2+6(x^2-2x+2)+1\)
\(y=-t^2+6t+1\)
この関数を平方完成すると
\(y=-t^2+6t+1\)
\(y=-{(t-3)}^2+10\)

\(t≥1\)の範囲でグラフを描くと、上の図のようになります。よって、上の図から\(t=3(x=1±\sqrt{2})\)の時、最大値10
この分野が苦手な人
2次関数は数学Ⅰの中でも苦手な人が多い分野だと思います。この2次関数の中でも、関数の最大値・最小値を求める分野で解けない人が多いのは、定義域などの範囲と文字を組み合わせた問題だと思います。場合分けをしなくてはならず、頭の中で考えて、式で書いているだけだと整理しづらい問題だと思います。
グラフを描いてみよう
2次関数の中で関数の最大最小を求める問題では、問題にグラフを描けと書いてなくてもグラフを描いた方が問題を整理できるので、グラフを描くようにしましょう。今は書く必要がないと感じる人も、問題を解いていて、分からないときにはグラフを描くようにしていきましょう。