こんにちは、あすなろスタッフのカワイです。
今回は、比例とは何か、について、例をもとに解説していきます。「そもそも比例って言葉の意味が分からない」という方は、以前の記事で意味を説明していますので、そちらを読んでみてください。
関連記事:【中1数学】関数ってなに?比例・反比例とは何なのか0から解説します!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
例1.図形の辺の長さと面積の関係を調べたい!
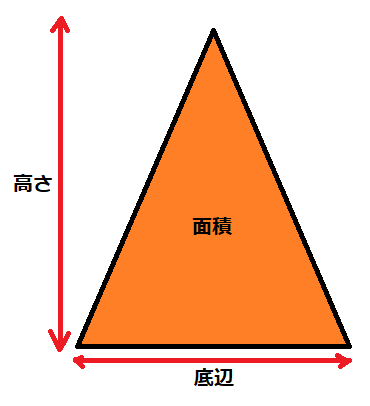
とある三角形の底辺は決まっているんだけど、高さが決まっていない…高さを変えると面積はどうなるんだろう…ということを、考えていきたいと思います。
まず、三角形の面積の求め方を考えますが、小学校で習った通り、
「底辺×高さ÷2」
で求めることができます。
今回知りたいのは、底辺の長さが変わると、面積がどう変わるのかということです。言い換えると、底辺の値を公式に入れると、面積の値がどう出てくるのかということですね。従って、入れる値である底辺を(x)、知りたい値(出てくる値)である面積を(y)としてみます。高さは4で一定とします。では、これらから式を作ってみましょう。
$$y=x×4÷2$$
(面積=底辺×高さ÷2)
これらを簡単にすると、
$$y=2x$$
と表せます。
これらに底辺の値を入れていくとどのような値になるのか分かりやすい様に、表にしてみましょう。
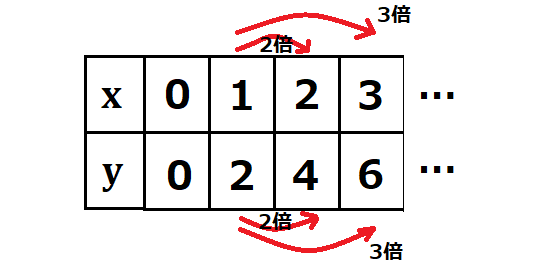
このように、\(x\)に上のような値を入れると、\(y\)が返ってきます。また、\(x\)の値を2倍、3倍にすると、\(y\)の値も同様に2倍、3倍になっています。
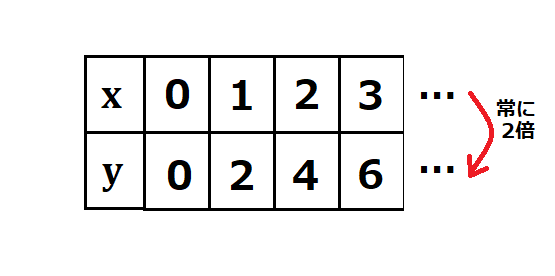
一方、\(x\)と\(y\)の値を比較すると、どの\(x\)の値に対しても、\(y\)の値は常に2倍となっています。
これらの関係は、元の関数を見てみればわかりますね。
\(y=2x\)なので、\(x\)に入れた値が2倍された値が\(y\)に出されます。
このような\(x\)と\(y\)の関係を、「\(y\)は\(x\)に比例する」といいます。
一般的に、ある\(y\)と\(x\)が比例するとき、その式の形は、
\(y=\color{red}{a}x\)
となります。この時の\(\color{red}{a}\)を比例定数と呼びます。
では、底辺の値が20の時、面積はいくつになるでしょうか。
答えは自明ですね。底辺の値の2倍が面積の値となるので、面積は40となります。
例2.車の時間と位置の関係を知りたい!
今度は、車が0の位置からある一定速度で走っていて、進む方向は変わらないとします。この車のある時間・位置が分かっているとした場合、どのように速度を知ることができるのか、考えてみましょう。
小学校の時に勉強した「道のり=時間×速さ」から求めることも可能ですが、今回は「ある一定速度」で走っているという点に着目して、比例の考え方で解いてみましょう。
ある一定速度\(a\)で、時間を\(x\)、位置を\(y\)とすると、これは
$$y=ax$$
と示すことができます。この形は例1で解説した通り、「\(y\)と\(x\)が比例関係」であることを表しています。従って、あるときの時間と位置が分かれば、速度を知ることができます。
例えば、\(3\)分で\(6\)kmの位置にいたとき、この速度はいくつでしょうか。
上の式から、$$6=3a$$となり、$$a=2$$とわかります。従って、
この車の速度は\(2\)km/分ですね。
次に、\(20\)分で\(10\)kmの位置にいたとき、この\(50\)分ではどの位置にいるでしょうか。
まず、上の式から、\(10=20a\)となり、\(a=0.5\)、すなわち、\(0.5\)km/分で走っているとわかります。次に、この車が\(50\)分走った時の位置が知りたいので、位置を\(y\)として式を考えると、$$y=0.5×50$$となります。
これを計算すると、$$y=25$$、すなわち\(25\)kmとわかります。
このように、比例であるとわかると、式の形が確定するので、比例係数を調べることで様々な場合の状態について知ることが可能です。
理解していただけたでしょうか?
まとめ
いかがだったでしょうか。比例の状態であるとわかると、他の様々な状態を知ることが可能になります。今まで勉強してきた方程式で十分対応することができると思うので、もし周りに同じように比例で考えることができるコトガラがあれば、自分で考えてみるのも面白いかもしれません。次回は、反比例の考え方について解説していく予定なので、今回の内容を理解した上で、チェックしてみてください!
やってみよう!
\(y\)は\(x\)に比例するとき、次の問題を解け。
- \(y=0\)、\(x=2\)のときの比例係数\(a\)はいくらか。
- \(y=6\)、比例定数\(a=-3\)のときの\(x\)はいくらか。
空の浴槽に水を入れて貯めていくとき、次の問題を解け。
- 浴槽の底から水面までの高さと時間が比例関係の時、水の貯まる速さはいくらか。なお、水を入れ始めてから\(5\)分の時、水面の高さは\(20\)cmとする。(答えの単位はcm/分)
- 水の貯まる速さが1.の答えで、水を入れ始めてから\(12\)分のとき、浴槽の底から水面までの高さはいくらになっているか。(答えの単位はcm)
答え
1.
- \(a=5\)
- \(x=-2\)
2.
- \(4\)cm/分
- \(48\)cm
最後までご覧いただきありがとうございました!
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。