こんにちは、あすなろスタッフのカワイです。
今回は因数分解について解説していきます!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校3年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
因数分解とは?
因数分解とは、多項式をいくつかの式の積で表すことです。
いくつかの式の積で表されたものを、すべて多項式の形にする展開と逆の操作になります。因数分解と展開の関係を図で表すと以下のようになります。

\((x+2)(x+1)\)から\(x^{2}+2x+3\)にする展開の操作では、乗法公式を使ったり、各項同士を地道に掛け合わせることで解くことができます。
因数分解はその逆ですが、四則計算するだけでは解くことができません。
なので、まずはカンタンなものから解説していきます。
共通因子のある多項式の因数分解
例1.\(x^{2}-3x\)
因数分解をするときは、まず全ての項に共通する要素(文字・数)があるかどうかを確認します。もしあれば、まずそれを()でまとめてあげます。
では、例題の式の因数分解を考えていきましょう。
$$x^{2}-3x$$
という式をみてみると、\(x\)が2つの項に共通していることがわかります。したがって、これをくくってみましょう。
$$x(x-3)$$
すると、このような形になります。多項式を複数の積で表すことが出来たので、これで因数分解完了です。
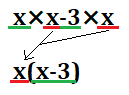
これを詳しくみてみると、このような形になります。赤い線で示した\(x\)が2つの項にあるため共通で、緑の線で示した\(x\)と\(-3\)が余り物になっているのでこれを足し合わせて()に入れます。
この形になることが疑問に思われるようであれば、\(x(x-3)\)を展開してみると、理解できるかもしれません。
似た例題をもう1題解いてみましょう。
例2.\(3y^{2}+9xy\)
式を確認すると\(y\)が共通して入っています。従って、\(y\)をそれぞれまとめる形で因数分解を進めていきましょう。
$$3y^{2}+9xy$$
$$y(3y+9x)$$
\(y\)でくくると、このようになります。
一見、これでいいような気がしますが、カッコの中にまだ共通因子があります。
カッコ内の項は\(3y\)と\(9x\)なので、実は\(3\)も共通因子です。
「\(3\)は1つの項にしかないじゃないか!」と思うかもしれませんが、\(9x\)というのは\(3×3×x\)であるので、両方の項に\(3\)が含まれていることになります。

では、これを踏まえて、\(3\)も因数分解してきます。
$$3y(y+3x)$$
これで因数分解完了です。
見た目で共通因子が見つけられない時は…?
先ほどの例題は、式を見ただけで何をまとめればいいのかが何となく判断できるものでしたが、そのような多項式ばかりではありません。
例えば、
$$x^{2}+2x+3$$
という式を見て、すぐ因数分解ができるか?というと、やり方を知らない限り難しいと思います。
ですが、この\(ax^{2}+bx+c\)の形の多項式の問題に対して、因数分解ができる公式があります!
因数分解の公式
- \(x^{2}+(a+b)x+ab=(x+a)(x+b)\)
- \(x^{2}+2ax+a^{2}=(x+a)^{2}\)
- \(x^{2}-2ax+a^{2}=(x-a)^{2}\)
- \(x^{2}-a^{2}=(x+a)(x-a)\)
覚える式が多くて面倒だと感じるかもしれませんが、この公式、展開するときに用いた乗法公式と全く同じです。なので、展開公式を覚えていれば、新たに覚えることはありません!
この式のうち、1番上の式の考え方を理解すれば、このような形の問題に対応できるようになります。
公式を用いた因数分解の考え方
例3.\(x^{2}+5x+6\)
この問題を解いていきます。上の公式を見ると、
$$x^{2}+(a+b)x+ab=…$$
となっているので、これらの式を照らし合わせると、
$$5=a+b$$
$$6=ab$$
となっていることが分かります。したがって、上の2式にあてはまる\(a\)と\(b\)が見つかれば、\((x+a)(x+b)\)の形で因数分解をすることができます。
\(a+b\)と\(ab\)のどちらから考えるべきかというと、足し算は無限に考えられ、キリがないので、必ず積分(\(ab\))の方から考えます。
\(ab=6\)となる\(ab\)の組み合わせは、
| \(a\) | \(b\) |
| \(1\) | \(6\) |
| \(2\) | \(3\) |
| \(-1\) | \(-6\) |
| \(-2\) | \(-3\) |
の4つです。ここで\(a\)と\(b\)が入れ替わっても意味合いは全く変わらないので、その組み合わせは除いています。
この中から、\(a+b=5\)となるものを探します。
| \(a\) | \(b\) | \(a+b\) |
| \(1\) | \(6\) | \(7\) |
| \(2\) | \(3\) | \(5\) |
| \(-1\) | \(-6\) | \(-7\) |
| \(-2\) | \(-3\) | \(-5\) |
これより、\(a=2\)・\(b=3\)のとき\(ab=6\)かつ\(a+b=5\)を両方満たすことが分かりました!
したがって、\(x^{2}+5x+6\)の因数分解は$$(x+2)(x+3)$$となります。
まとめ
- 多項式を因数分解するときは、まず括れるもの(共通因子)を探そう!
- 因数分解の公式(乗法公式の逆)を用いることで因数分解できる!
因数分解は慣れるまでは苦手に感じるかもしれませんが、慣れてくると公式を考えずに解けるようになると思います。
別の記事で、他の多項式の因数分解をしていくので、良かったらそちらも読んでみて下さい!
やってみよう!
この多項式を因数分解してみよう
- \(x^{2}+5x\)
- \(4ax^{2}-8xy\)
- \(x^{2}+7x+6\)
- \(x^{2}-3x+2\)
答え
- \(x(x+5)\)
【解説】\(x^2\)と\(5x\)という2つの項に共通しているのは\(x\)である。そこで、\(x\)でくくってあまりもの同士を足し合わせると\(x(x+5)\)となる。 - \(4x(ax-2y)\)
【解説】\(4ax^2\)と\(-8xy\)という2つの項に共通しているのは\(4x\)である(\(8\)は\(4×2\)と考えられる)。\(4ax^2\)と\(-8xy\)はそれぞれ\(4x×ax\)と\(4x×(-2y)\)となるため、\(4x\)以外の部分をそれぞれ足し合わせたものを()でくくると\(4x(ax-2y)\)となる。 - \((x+1)(x+6)\)
【解説】因数分解後を\((x+a)(x+b)\)(ただし\(a≦b\))とする。\(a+b=7\)かつ\(ab=6\)となるのは\(a=1, b=6\)の時なので、答えは\((x+1)(x+6)\)となる。 - \((x-2)(x-1)\)
【解説】因数分解後を\((x+a)(x+b)\)(ただし\(a≦b\))とする。\(a+b=-3\)かつ\(ab=2\)となるのは\(a=-2, b=-1\)の時なので、答えは\((x-2)(x-1)\)となる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。