こんにちは、あすなろスタッフのカワイです。
今回は、素因数分解とそれを用いて平方根を整数の形にする方法について解説していきます。
今回も頑張っていきましょう!
関連記事:【中3数学】平方根ってなんだろう?正方形を用いて、平方根の意味を解説します!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校3年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
素因数分解とは?
素因数分解とは、一つの数字をいくつかの素数の積で表す操作のことをいいます。
因数分解では、多項式をいくつかの単項式の積で表す操作だったので、これは数字でそれをするものと考えることができます。
因数分解の場合は決まった組み合わせでしか表すことができなかったように、素因数分解も結果は1つに決まります。
素数の復習
素数とは、その数が\(1\)とその数の2つでのみ割ることができる数のことです。小さい数から\(2,3,5,7,11…\)と続き、無限にあるといわれています。
では、これを用いて、実際に素因数分解してみましょう。
具体的に素因数分解をしてみる
例.\(180\)
\(180\)という数を素因数分解して、素数だけの積の形にしてみましょう。
\(180\)は偶数なので、\(2\)で割ることができます。したがって、
$$180=2×90$$
\(90\)も同様に偶数であるので、
$$180=2×2×45$$
となります。\(45\)は5で割ることが出来るので、
$$180=2×2×5×9$$
\(9\)は\(3×3\)で表すことが出来るので、
$$180=2×2×3×3×5$$
となります。上記の数はすべて素数となっているので、これ以上分解することが出来ません。
最後に、同じ素数が複数ある場合は、それらを累乗の形にしなければなりません。今回の場合、\(2\)と\(3\)がそれぞれ2つあるので、
$$180=2^{2}×3^{2}×5$$
と表します。これで\(180\)の素因数分解は完了です。
ここで注意しなければならないのが、この分解の中に\(×1\)を含めてはいけません。\(1\)は素数ではないからです。
ところで、素因数分解によって数を分解した因数のことを素因数といいます。素因数のみで表される状態に分解するから素因数分解ということですね。
もっと簡単な素因数分解の方法はこちら!
筆算のような形で書いていく方法でも素因数分解をすることができます!
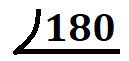
まず、\(180\)と書いた後、\(180\)を割ることが出来る素数を探します。今回は\(2\)を選択しました。(180を割りきることができる他の素数を入れてもいいです)
割る数を割られる数の左隣に、割った後の商を下に書きます。
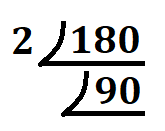
これをどんどん続けていくと、
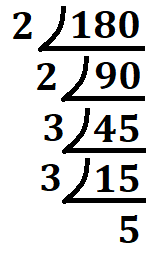
となります。商が素数になった時点で計算終了です。途中の過程が違っても、最後の素数は必ず同じになります。
最後に、割った数と最後に残った数が素因数分解を構成する要素になります。
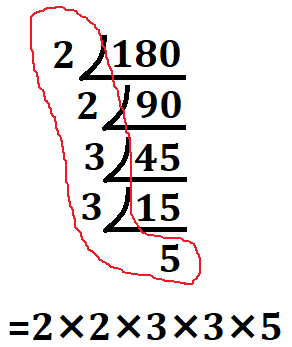
あとは、先ほど説明した2乗の形に変形すれば完了です。
平方根の素因数分解の利用
では、素因数分解をどのように平方根に利用することが出来るのか紹介していきます。
結果から先にお伝えすると、平方根の形から「整数\(×\)平方根」や「整数」、「分数」の形にすることが出来ます。
どのような原理であるかを下に示します。
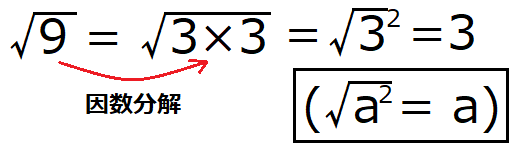
かんたんに説明すると、根号内の数字を素因数分解して、2乗の素数で表すことができれば、それを整数として平方根の外に出すことが出来ます。
根号の外に出して整数や分数にするメリットは、その数の具体的な数を知ることがかんたんになることです。
例えば、\(√16\)と\(4\)という同じ大きさの数があるとき、\(4\)の方が明らかに分かりやすい形ですよね。
例2.\(√150\)
\(√150\)内の数字\(150\)をまず素因数分解していきます。
\(150\)は偶数なので\(2\)で割ることが出来ます。従って、
$$150=2×75$$
\(75\)は\(5\)で割ることが出来るので、
$$150=2×5×15$$
\(15\)は\(3×5\)と表されるので、
$$150=2×3×5×5$$
となります。これで素因数分解は完了です。この結果に根号\(√\)をつけてみると、
$$√2×3×5×5$$
となります。この中で同じ数字が2つあるもの(2乗とすることが出来そうなもの)を探してみると…\(5\)が当てはまります。これを2乗して根号の外に出してみると、
$$√5^{2}×√2×3$$
これはそのまま
$$5√2×3$$
となります。残りの\(√2×3\)は\(√6\)に戻してしまいましょう。従って、この結果は
$$5√6$$
となります。
まとめ
- 素因数分解とは、数字を素数の積で表すことである。
- 平方根に用いることで、平方根のみの形を「平方根×数字」や数字のみの形に変形させることができる
いかがでしたか?素因数分解を行うことによって、その数字がどの数字の掛け合わせによって出来ているのかを見ることが出来たり、平方根をより容易な形に変形することが出来ることが分かりました。
次回からは、今回学んだ素因数分解を用いて、平方根の乗除計算を行っていきますので、よろしければ次の解説記事も読んでみてください。
やってみよう!
次の整数を素因数分解しよう。
- \(30\)
- \(75\)
- \(100\)
- \(252\)
次の平方根を、整数×平方根、または整数の形にしてみよう。
- \(√45\)
- \(√56\)
- \(√121\)
答え
次の整数を素因数分解しよう。
- \(2×3×5\)
【解説】\(30\)を\(2\)で割ると\(15\)、\(15\)を\(3\)で割ると\(5\)となることから、\(30\)は\(2\)と\(3\)と\(5\)の積で表されることが分かる。 - \(3×5^{2}\)
【解説】\(75\)を\(5\)で割ると\(15\)、\(15\)を\(3\)で割ると\(5\)となることから、\(75\)は\(3\)と\(5\)と\(5\)の積で表されることがわかる。\(5\)を累乗でまとめると答えの形になる。 - \(2^{2}×5^{2}\)
【解説】\(100\)を\(2\)で割ると\(50\)、\(50\)を\(2\)で割ると\(25\)、\(25\)を\(5\)で割ると\(5\)なので、\(100\)は\(2×2×5×5\)で表せることがわかる。\(2\)と\(5\)をそれぞれ累乗で表すと答えになる。 - \(2^{2}×3^{2}×7\)
【解説】\(252\)を\(2\)で割ると\(126\)、さらに\(2\)で割ると\(63\)、これを\(3\)で割ると\(21\)、これを\(3\)で割ると\(7\)となる。これより\(252\)は\(2×2×3×3×7\)で表せることが分かる。これを累乗の形で表すと答えになる。
次の平方根を、整数×平方根、または整数の形にしてみよう。
- \(3√5\)
【解説】根の中身を素因数分解すると\(45\)は\(3×3×5\)で表される。\(3\)が2つあることから、これを根の外に出して\(3\)、根の中には\(5\)が残るから、答えは\(3√5\)となる。 - \(2√14\)
【解説】根の中身を素因数分解すると\(56\)は\(2×2×14\)で表される。\(2\)が2つあることから、これを根の外に出して\(2\)、根の中には\(14\)が残るから、答えは\(2√14\)となる。 - \(11\)
【解説】\(121\)は\(11×11\)で表されることから、根の外に出して答えは\(11\)となる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。