こんにちは、あすなろスタッフのカワイです。
今回は、平方根とはどのようなものなのかを正方形を使って理解することが出来るように解説していきます。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校3年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
平方根とは?
平方根は、
「ある数\(x\)を2乗すると\(a\)となるとき、その\(x\)を\(a\)の平方根という」
と定義されているものです。
文章を読むだけでは正直よくわかりませんね。しかし、平方根の考え方自体には既に触れてきています。正方形の面積と辺の長さの関係を用いて、平方根の意味と、それが必要な理由について解説していきます。
ある正方形の面積\(a\)について考える
正方形の面積は「\(辺の長さ×辺の長さ=面積\)」すなわち、「\(辺の長さ^{2}=面積\)」で求めることが出来ます。
例えば、辺の長さが3の正方形の面積を考えたとき、その面積は、
$$3^{2}=9$$
と求めることができますね。
では、逆に面積が9の正方形の辺の長さはどれだけか、をどのように求めるかというと、
$$9=3^{2}$$
のように、前の操作の逆をしてあげればできるわけです。
これを一般化すると、ある正方形の面積\(x\)がわかっているとき、その正方形の辺の長さを\(a\)とすると、
$$x=a^{2}$$
と表すことが出来ます。
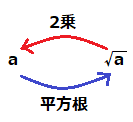
このように、ある数\(x\)があって、その数を\(a\)の2乗という値でなんとか表現したい時、この\(a\)のことを\(x\)の平方根といいます。
面積が23の正方形の辺の長さを考えてみよう
では、今説明した考えを踏まえて、面積が23の正方形の辺の長さを考えていきましょう。
辺の長さを\(x\)とすると、式は、
$$23=x^{2}$$
となります。
さて、この\(x\)に当てはまる数を考えてみます。
| \(x\) | \(x^{2}\) |
| \(3\) | \(9\) |
| \(4\) | \(16\) |
| \(5\) | \(25\) |
| \(6\) | \(36\) |
まず、2乗すると\(23\)になりそうな整数を考えてみます。見た感じ、整数の2乗では\(23\)にはなりません。しかし、\(4^{2}\)は\(16\)、\(5^{2}\)は\(25\)なので、\(4\)と\(5\)の間に答えがありそうだ、ということは分かりますね。では少数の範囲に拡大して考えてみましょう。
| \(x\) | \(x^{2}\) |
| \(4.6\) | \(21.16\) |
| \(4.7\) | \(22.06\) |
| \(4.8\) | \(23.04\) |
| \(4.9\) | \(24.01\) |
このようになりました。\(4.8\)を2乗した値が\(23\)にほど近いですが、ぴったりではないのでまだ駄目です。しかし、\(4.7\)と\(4.8\)の間に答えがあるはずです。
| \(x\) | \(x^{2}\) |
| \(4.78\) | \(22.8484\) |
| \(4.79\) | \(22.9441\) |
| \(4.80\) | \(23.0400\) |
結論を出すと、2乗して丁度\(23\)となる数は、少数で完全に表す方法がなく、無理数と呼ばれる数字となります。
少数で表すことが出来ないのであれば、表すことは出来ないのか?というと、そういうわけではありません。ここで平方根というものを用いるのです。
$$\sqrt{23}$$
と示すことで「二乗すると23となる数」を示すことが出来ます。
この\(\sqrt{}\)のこと根号といい「ルート」と言います。なので、上の\(\sqrt{23}\)については「ルート23」ということになります。
ある数字\(a\)に根号をつけると、「2乗すると\(a\)となる数」を表します。
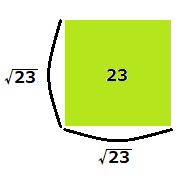
さて、面積が23の正方形の辺の長さは\(\sqrt{23}\)が正解となります。
少数や分数で表さないとズルくない?と思うかもしれませんが、これもれっきとした数字の一つです。
平方根は2つある
最初に説明した話に少し戻してみます。ここまでの文脈でいくと、正方形の面積が9の辺の長さは、
$$\sqrt{9}$$
と表すことも出来ます。すなわち、
$$\sqrt{9}=3$$
と表現することが出来ます。
ここで図形からいったん離れて、単なる数式として扱うならば、\(9\)の平方根はもう1つ存在します。それは負の数の場合です。
乗法では、\(負の数×負の数=正の数\)となることから、\(-3\)は\(9\)の平方根となります。
\(3\)と\(-3\)の共通点は「絶対値が等しい」というところにあります。従って、一つ平方根を見つけたら、同じ絶対値 かつ 異なる符号の値がもう一つの平方根になります。
忘れやすいので、注意してください!
まとめ
- 平方根とは、ある数\(x\)を\(a\)の2乗で表現したいときの\(a\)のことをいう!
- 平方根は絶対値が等しい正と負の2つが存在する。
やってみよう!
次の値の平方根を答えてみよう
- \(13\)
- \(5\)
- \(9\)
こたえ
- \(±\sqrt{13}\)
- \(±\sqrt{5}\)
- \(±\sqrt{9}\) または \(±3\) 【解説】平方根は正の数と負の数の二つがあるので忘れないようにしましょう。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。