こんにちは、家庭教師のあすなろスタッフのカワイです!
今回は、“”確率“”とはなにか?身近ではどのような事に使われているのか?ということに重きを置いて、初めて確率という言葉を目にした人でも分かるように解説していきます!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
確率とは?
偶然起こるすべての現象を1としたときに、あることがらの期待される程度を数字で表したものを、その確率といいます。
言葉で表すのは難しいので、例を挙げて説明していきます!
例1:コイントス
コイントスは、コインを投げて、裏が出るか表が出るかを当てるゲームです。
さて、あるコインを1回投げると、表と裏のどちらが向くのか考えてみましょう。
さて、どちらが出ると思いますか?
絶対に表!絶対に裏!と言い切ることはできませんよね。みなさんの今までの経験的にも、表も裏も同じくらいに出てくるのだと思います。
(ちなみに、このように表も裏が同じ程度に期待できる場合、これを同様に確からしいといいます。)
確率は、あることがらについて、すべてのパターンを足し合わせると1となるので、
表が出る確率を\(\frac{1}{2}\)、裏が出る確率を\(\frac{1}{2}\)と表すことになります。(表、裏以外のことは起こらないはずですからね)
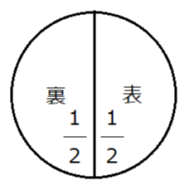
このように、ものごとが発生する前から、その結果がどのようになるのかを、1に対する数の割合で数学的に予想すること、これを”確率”といいます。
ちょっと応用
さて、今の例では、1回投げたら半分の確率で表が、半分の確率で裏が出ることが分かりました。
ということは、10回投げたら、5回表が出て、5回裏が出ます!
と言い切れるかというと、これもそういうことではありません。あくまで理論的にそうなるだけで、実際には「表が3回、裏が7回」となったり、「表が6回、裏が4回」となったりすることも十分に考えられます。このような\(\frac{表(裏)になった回数}{すべての試行回数}\)のことを相対度数といいます。
試行回数を増やせば増やすほど、確率の値(1/2)に近づいていくのです。
例2:サイコロ
コイントスと同様に、サイコロの目の確率も考えてみましょう。
サイコロの目は1から6まであります。これを1回振った時に、1の目が出る確率はどれくらいでしょうか?
前提として、サイコロは1の目も6の目もその他の目も、同様に確からしいとします。
ですから、全ての場合(1)を6等分するので、どの目の確率も\(\frac{1}{6}\)となります。
従って、1回振って1の目が出る確率も\(\frac{1}{6}\)となります。
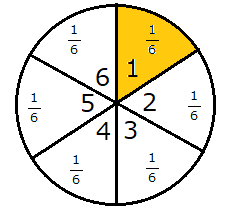
図にすると上のようになります。
さて、今度は5以上が出る確率も考えてみましょう。
5以上とは、サイコロの場合5,6になります。この確率というのは、5が出る確率と6が出る確率の足し算で表すことが出来るので、
\(\frac{1}{6}+\frac{1}{6}=\frac{1}{3}\)となります。
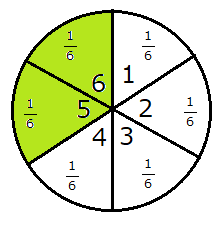
何故足し算で表すことができるのか?と思う人は、図で書いてみると一目瞭然です。6が出るという事柄と5が出るという事柄が全く被らないので、このように足し算で表すことができるのです。
これらから分かった方もいるかもしれませんが、確率は次のような式で表すことができます。
\(確率=\frac{○○という事象が起こる数}{事象のすべての数}\)
今回の5以上の目が出る確率の場合、この式は
\(5以上の目が出る確率=\frac{5以上の目の数}{すべての目の数}\)
と書けますね。
まとめ
- 確率とは、とあることがらのすべての場合の数である特定の場合の数で割ったものである
- あらゆる事象が同じ程度に期待できる場合、それを同様に確からしいという
いかがでしたか?確率という言葉を聞くと難しいとイメージされる人が多いかもしれませんが、サイコロやコインなど単純な場合を考えると、”意外と解けそう!”と思う人が結構いるのではないでしょうか。
確率を勉強することで、あらゆる場合において、どの選択をすればいいのかを、理論的に考える重要な手助けとなるので、実生活にも生かすことができます。
今後は、確率の考え方をもう少し深めていきますので、次の解説ページも是非読んでみて下さいね!
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。