こんにちは、家庭教師あすなろスタッフのカワイです。
今回は”合同”について学習していきます。
合同は、図形と図形の関係を定義づける重要な考えの1つです!
中学数学の入試でよく登場する「証明」で必要になることもあるものなので、しっかりその意味について理解していきましょう。
それでは今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
“合同”とは?
2つ以上の図形があり、それらの図形を重ね合わせると完全に一致するとき、それらの図形は「合同である」といいます。言葉を変えて言うと「平行移動」「回転移動」「対称移動」で重ねることができる図形を合同といいます。
早速図を見ながら確認していきましょう!
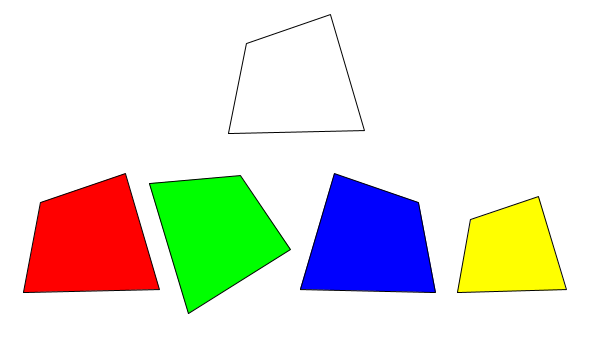
このような複数の四角形があります。下段の色付きの四角形を移動させて、上段の無色の四角形とぴったり合わせることが出来るかを確認してみましょう。
上で定義した通り、ぴったり重なりあえば合同、重なり合わなければ合同ではない、ということになります。では早速やってみましょう。
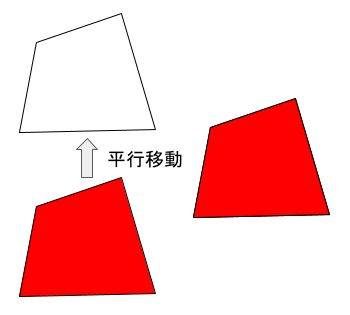
赤の図形は、向きと形状、大きさは全く同じですが、場所が違います。これを平行移動してみると、確かに重なります。従って、これらは合同です。
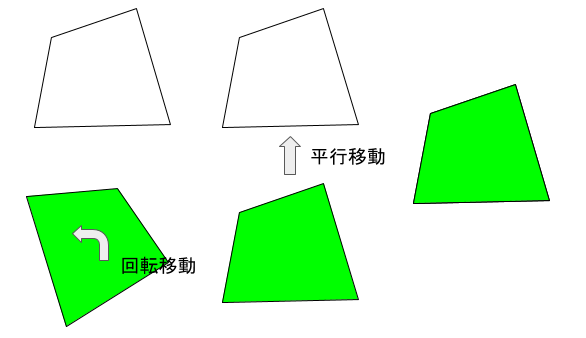
緑の図形は、向きは違いますが、形状や大きさは全く同じようです。これを回転移動してみると、赤の図形のように、向き、形状、大きさがすべて一致しました!後は赤と同様に重ねることが出来るので、これも合同です。
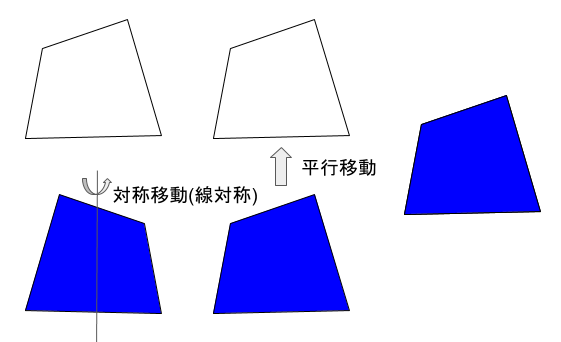
青の図形は、形状、大きさは同じで、向きも同じようですが、どうやら鏡絵のようになっています。これは対称移動してみると、向きが一致していることが分かります!従って、これは合同です。
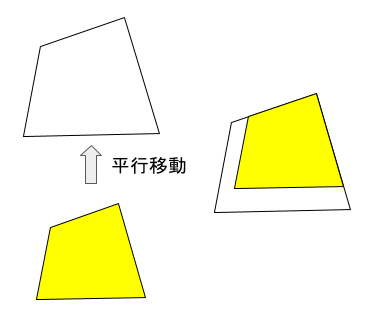
黄の図形は、形状、向きは同じようですが、大きさが異なっています。これは平行移動して重ねてみると、当然ピッタリは重なりません。従って、これは合同ではないということになります。
(ちなみに、上の図形の関係は「相似」といい、中学3年の数学で勉強する重要な性質をもったものになります。今回は合同についての解説なので説明しませんが、名前だけでも覚えておくとよいでしょう。)
数式での合同の示し方
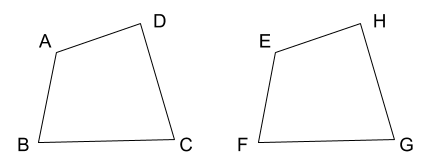
上図のような四角形ABCDと四角形EFGHが合同であることを数式で示すときは、
\(四角形ABCD≡四角形EFGH\)
とします。
「≡」は新しい記号だと思いますが、イコール(\(=\))に一本線が加わっただけなので、そこまで違和感は無いでしょう!
また、それぞれの図形の対応する角について、順番を揃えて書かなければならないというルールがあります。例えば、上の式では角Aと角Eが等しくなっていて、同様に角Bと角F、角Cと角G、角Dと角Hが等しくなっています。(なっていなければいけません!)
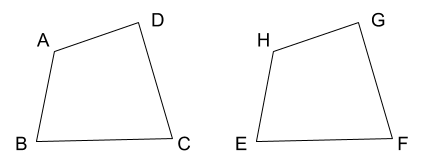
さて、上のような合同な図形を表すときは、どうすればいいでしょうか。
ここで上と同じように、
\(四角形ABCD≡四角形EFGH\)
としたら、それは間違いです!
対応している角に合わせて、
\(四角形ABCD≡四角形HEFG\)
と書かなければなりません。逆に言えば、角が対応してさえいればいいので、
\(四角形BCDA≡四角形EFGH\)
や
\(四角形CDAB≡四角形FGHE\)
とするのは全く問題ありません。
合同な図形の性質
合同な図形であると何が分かるのかというと、合同の定義から明らかですが、
対応する角・辺が等しい
ということになります。合同な図形があって、片方の図形の辺の長さや角が分かっていたら、それと合同である図形の対応する角・辺の長さが分かるということです!
まとめ
- 合同とは、「2つ以上の図形がピッタリと重ね合わせられるときの関係」をいう。
- 合同を数式で表すときは、「≡」を用いる。
- 合同な図形は対応する「角」「辺の長さ」が等しくなる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。