こんにちは、あすなろスタッフのカワイです！
式と計算という単元では、単項式や多項式といった文字式についての計算を学んできたと思います。今回はその集大成として、文字式を使った「式による説明」のしかたについて解説していきます！
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
例題1.連続した整数の和
問題：連続した3つの整数の和が3の倍数になる事を説明せよ
連続した3つの整数を足し合わせたら3の倍数になる、という事を、どのように説明すればいいでしょうか。取り敢えず、具体的な整数から考えてみましょう。
例えば、\(1,2,3\)ですね。3つの数を足し合わせると、\(1+2+3=6\)であり、\(6\)は3の倍数ですから、合っていますね！次に、\(5,6,7\)についても考えてみましょう。3つの和は、\(5+6+7=18\)となります。\(18\)は確かに3の倍数なので、確かに正しいということが分かります。
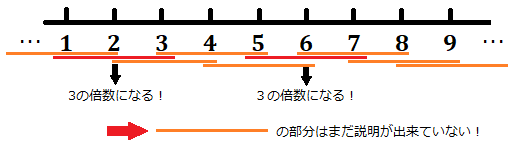
「よーし、だから、3つの整数の和は3の倍数になるんだ！」という風になれば良いのですが、上で挙げたのはあくまで\(1,2,3\)と\(5,6,7\)の場合であって、もしかしたら、他の組み合わせでは違うかもしれないので、十分な説明とは言えません。従って、全ての整数の場合について同じように説明できる方法で表す必要があります。
それが、文字式を使った方法です！文字式は非常に便利なんですよ。
では、どのようにすればいいのか解説していきましょう。
まず、文字にどんなものが入るのか、決めておく必要があります。文字を\(n\)と置くと、今回の場合は「整数」全てについて説明したいので、\(n\)に入る事が出来るのは全ての整数という事にします。(文字は\(n\)でなく\(x\)や\(y\)などの他の文字でも構いません)
次に、連続した3つの整数を用意する必要があります。今回は、\(n\)を連続する数のうち真ん中の数としましょう。
すると、その前後の数を\(n-1,n+1\)と表すことが出来ます。このようにして、連続する3つの整数\(n-1,n,n+1\)を用意することが出来ました！ここまで理解していただけたでしょうか？
では、この3つの整数を実際に計算していきましょう！
$$(n-1) + n + (n+1) = 3n$$
以上より、この計算の和は\(3n\)となります。\(3n\)とは
$$3n = 3\times{n}$$
という事なので、\(n\)にどのような整数が入っても3の倍数になる事が分かると思います。
以上より、「連続した3つの数の和は3の倍数になる」という説明が出来ました！
このように、文字を利用することによって、ただの数字では表しきれないような、多くの場合についての説明をすることが出来るようになります！
もしこれでもよくわからないという人は、nに実際に整数を代入してやってみて下さい。どのような仕組みになっているのか理解しやすいと思います。
例題2.位の数を入れ替えた数の和
問題：2桁の自然数とその10の位と1の位を入れ替えた数の和が11の倍数になる事を説明せよ
先程と同様、一旦、具体的な数字で考えてみましょう！
\(12\)という数字を考えると、10の位と1の位を入れ替えた数は\(21\)ですね。この2つを足し合わせると、\(12+21=33\)となり、\(33\)は\(11×3\)である為、確かに11の倍数となる事が分かります。
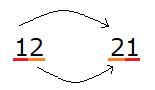
一見難しそうですが、文字に置き換えてしまえば意外と簡単に解くことが可能です。
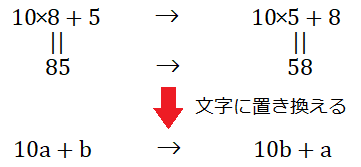
今回は、10の位の数字と1の位の数字を入れ替えるので、それぞれの位の数字について文字を置いておくと考えやすそうですね。従って、10の位の数字を\(a\),1の位の数字を\(b\)と置いてみます。この整数を表すには、\(10a+b\)と書けば問題がありませんね。(例えば、\(85\)という数字を10の位と1の位に分けて表す場合、\(8×10+5\)と書くことが出来ます。)従って、ひっくり返した時の数字は\(10b+a\)となります。もし理解が出来ていないようだったら、\(a\)と\(b\)に一桁の自然数(1とか2とか3とか)を入れて、\(10a+b\)と\(10b+a\)を考えてみて下さい！
さて、計算に必要な2つの自然数を置くことが出来たので、実際に計算をしていきます！
$$(10a+b) + (10b+a) = 11a +11b$$
$$=11(a+b)$$
計算を進めていくと、上のように11でくくることが出来る事が分かります！という事は、11の倍数であるという事が説明できました！
文字の置き方のテクニック
文字式を利用した問題は様々ありますが、実際の文字の置き方についてはそうバリエーションが多くありません。いくつか典型的な置き方を列記していきますので、見ていきましょう！
偶数・奇数が出てくる問題
偶数とは2の倍数のことなので、整数を\(n\)とすると、\(2n\)でOKです！もし連続する場合は、\(2n-2\)や\(2n+2\)など、2ずつ増やしたり減らしていけば、前後の偶数を表すことが出来ると思います！
奇数の場合は、偶数と隣り合った数となっているので、整数を\(m\)とすると\(2m-1\)や\(2m+1\)と表すことができると思います。偶数同様、ここから2増やしたり減らしたりすることで、前後の奇数も表すことが可能です！
桁を入れ替える問題
例題2でも示しましたが、文字を置くターゲットを各桁の数にしてあげればいいです。例えば、4桁の自然数の各位を文字で表したい場合、1000の位から順に\(a,b,c,d\)と置くと\(1000a+100b+10c+d\)と書くことが出来ます。
商の余りを表す問題
ある整数を割ったときの余りが～。という問題がよくあります。そのような整数はどう記述すれば良いでしょうか。今回はある整数xを3で割った商が\(a\)、余りが\(b\)となるという条件とします。
すると、\(x=3a+b\) (b<3) と記述すればOKです！ここで、余りの数が割る数よりも大きくなることは無いので、(余り<割る数)という条件を付けてあげる事に注意が必要です！
まとめ
・問題となる数を文字で置くところがポイント！
問題が解けるか解けないかは、文字の置き方次第になります。基本的には上で紹介した例題のような問題がよく出てくるので、慣れていけばそう難しいことはありません。
文字と式については、今回が最後になります。今後の単元にもこの単元で学んだことがとても多く出てきます。不安な人は読み返したり、例題を自力で解いてみたりして、理解を深めていってください！
やってみよう！
問題
- 連続した4つの整数の和は偶数になる事を説明せよ
- 同じ月のカレンダーで斜めに並んだ3つの数の和は3の倍数となる事を説明せよ
答え
-
連続した整数のうち、一番数が小さいものをnとする。すると、連続した残り3つの数は、小さい方から\(n+1,n+2,n+3\)と表せる。
これらの和を導出すると、
$$n+(n+1)+(n+2)+(n+3)=4n+6$$
$$=2(n+3) $$
となる。\(n+3\)は整数であり、\(n+3\)に2が掛けられていることから、この和は2の倍数、すなわち偶数であることが分かる。
従って、連続した4つの整数の和は偶数となる。
- 斜めに3つ並んだ数のうち、真ん中の数をnとする。すると、右斜め上、左斜め下の数をそれぞれ\(n-6,n+6\)
と表せる。
これらの和を導出すると、
$$(n-6)+n+(n+6)=3n$$
となる。\(3n\)は整数であり、3の倍数であることから、同じ月のカレンダーで斜めに並んだ3つの数の和は3の倍数となる。
最後までご覧いただきありがとうございました。
｢数学でわからないところがある｣そんな時に役立つのが、勉強お役立ち情報！
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
