こんにちは、あすなろスタッフのカワイです。
今回は、ここまでの文字と式のルールを用いて、一次式の足し算・引き算のやり方について解説していきます!
文章で表された数量の関係を、文字式で表す場合の解説はこちらの記事
を参考にしてください。
では、今回も一緒に頑張って学んでいきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
一次式の計算は図形の面積の足し合わせとして考える
文字式の計算、というと何か難しそうなイメージがありますが、これを図形という形に置き換えれば意外と簡単に考えることができます!
例として、\(4\times{3}+5\times{3}\)を考えてみましょう。
\(3\)が\(4\)にも\(5\)にもかかっていますね。では、\(3\)を縦の長さとした長方形を二つ作ることが出来そうです。
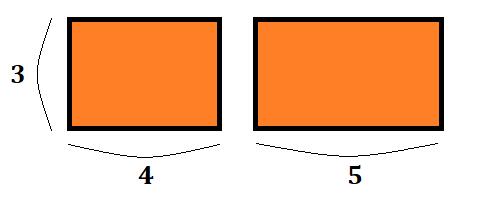
このように、縦の長さが\(3\)、横の長さが\(4\)、\(5\)となる図形が出来ました。見た目的にくっつけてしまっても問題なさそうです。では、繋げてみましょう。
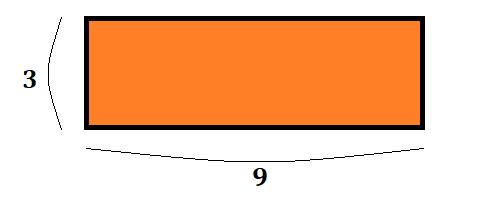
縦の長さが\(3\)、横の長さが\(9\)となる長方形が出来ました。この面積を計算してみると、
$$3\times{9}=27$$
となります。一方で、式で計算していくと、\(3\times{4}+3\times{5}=12+15=27\)となり、値は同じになります。問題なさそうですね。
では、次は文字を含んだ式としてこれを考えてみることにしましょう!
元の式の\(3\)を\(x\)に代えてみると、
$$4x+5x$$
となります。これをさっきと同じ長方形として表してみましょう!
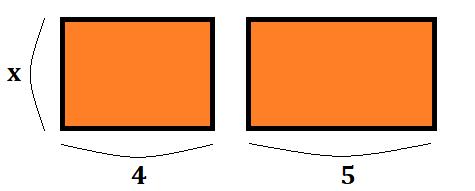
この通り、変わったところは縦の長さだけです。見た感じ、\(3\)だった時と同じように、長方形を合体させることが出来そうな気がしませんか…?
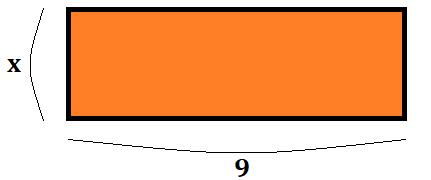
ここまでの流れで分かったかもしれませんが、出来ます。\(x\)には任意の値が入ることが出来るので、ここには当然\(3\)も入ることができるわけです。本質は変わっていないんですね。
では、この面積は…?というと、\(9x\)と書くほかありません。とすると、
$$4x+5x=9x$$
となります。
この1次式の計算、実は、文字の部分が同じであれば、文字の前に付いた数字(係数)同士の計算をするだけで完了です!
遠回りの説明でしたが、とても簡単なんです!
では、今度はちょっとだけ複雑な問題を出してみます。
異なる文字を含んだ1次式の計算
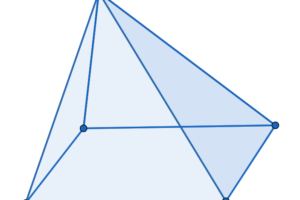
$$3x+2y+2x+4y$$
このように、2つ文字の入った式の計算を考えてみましょう。一応、先程と同様、図も載せておきますね。
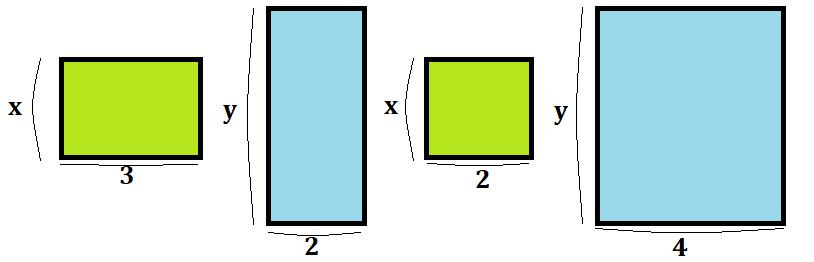
とりあえず、同じ数同士の計算は、上でやった通り係数を足すだけで良さそうなので、式を簡潔にまとめてみましょう。
$$x\times{5}+y\times{6}=5x+6y$$
さて、計算はここで終了です。\(x\)や\(y\)に入る値が決まっていないので、勝手にまとめてしまうことはできません。図で表すとこうなります。
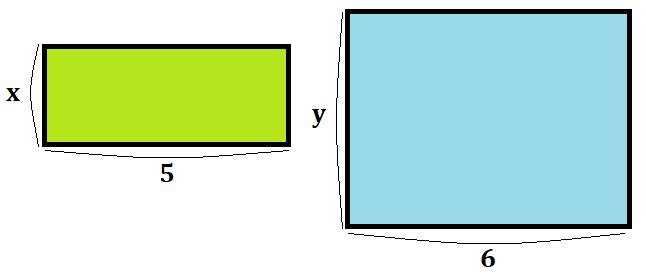
基本的に、同じ文字同士であれば係数の足し算・引き算が可能で、文字が違ったり、文字が同じでも次数が違えば計算を進めることはできません。
ちょっとだけ応用
ここまでは足し算のみ扱ってきましたが、引き算も同様に行うことが可能です!
例えば、\(16x-9x\)であれば、同じ文字同士の計算なので、係数の\(16-9=7\)を計算したら、答えが\(7x\)と出てきます。
次に、このような問題ではどうでしょうか。
$$3x+9-2x-7$$
文字を含んだ項以外に、数字だけの項もあります。
これらは、全部種類ごとにまとめて計算をしていきましょう!
$$3x+9-2x-7$$
$$=3x-2x+9-7$$
$$=x+2$$
このように、今までの足し算と同様に計算することができます!
まとめ
- 同じ文字の項同士の係数を計算すればOK!
- 異なる文字の項はまとめることが出来ない!
いよいよ数学らしくなってきましたが、次回は乗法・減法に範囲を拡大して学習していきます。しっかりと勉強をして、今回の内容を抑えてください。お疲れ様でした!
やってみよう
次の式を計算してみよう。
- \(3x+7x\)
- \(6x-8x\)
- \(3x+2y-x+3y\)
- \(5x+4-2x+3\)
- \(4y-3-5y+6\)
こたえ
- \(10x\)
- \(-2x\)
- \(2x+5y\)
- \(3x+7\)
- \(-y+3\)
最後までご覧いただきありがとうございました!
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。