数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。今回は高校1年生の数学の中でもずけいの性質について書いていきたいと思います。この図形の性質という単元では主に三角形や円について成り立つ定理や言葉の意味などで新しいものが出てきます。図形の形自体は複雑なものではないのでしっかりと理解するようにしましょう。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
わからない…を“わかる!”に変える家庭教師
「勉強がわからない」そんな悩みは、あすなろ関西の家庭教師が解決!一人ひとりに合った勉強方法で、小学生から高校受験までサポート!
たった15分の勉強で、これまでの3倍の効果を実感!そんな効率的な学びを、無料体験で試してみませんか?

=もくじ=
図形の性質
この図形の性質では新しい定理や用語、どのような性質があるかがたくさん出てきます。この単元で出てくる定理や用語、性質はそれほど難しいものはありませんが、内分、外分、外心、内心、重心など、これから先によく使う内容がたくさん登場します。ひとつずつ確実に理解していくようにしましょう。
内分と外分
m、nを正の数として、点Pが線分AB上にあって、
AP:PB=m:n
が成り立つとき、点Pは線分ABをm:nに内分するといいます。
また、点Qが線分ABの延長上にあって、
AQ:QB=m:n
が成り立つとき、点Qは線分ABをm:nに外分するといいます。
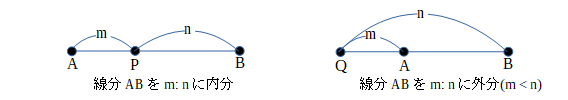
中点連結定理
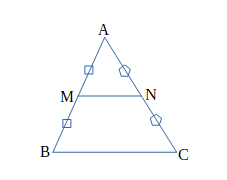
△ABCについて、辺AB、ACの中点をそれぞれM、Nとするとき、次の2つが成り立つ。
①\(MN//BC\)
➁\(MN=\frac{1}{2}BC\)
外接円と外心
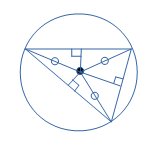
三角形の3辺の垂直二等分線の交点を外心といいます。外心は三角形の3つの頂点から等距離にあるので、外心を中心とした3つの頂点を通る円が存在し、その円を外接円といいます。
下の図の真ん中の黒い点が三角形の外心です。
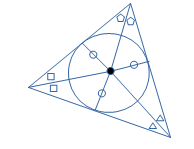
内接円と内心
三角形の内角の二等分線の交点を内心といいます。内心は三角形の3辺から等距離にあるので、内心を中心として3つの辺に接する円が存在し、その円を内接円といいます。
下の図の黒い点が三角形の内心です。
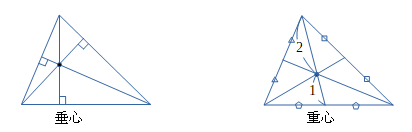
重心・垂心
三角形の中線の交点を重心、3つの頂点からの垂線の交点を垂心といいます。
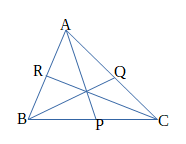
メネラウスの定理
△ABCの辺BC、CA、ABまたはそれらの延長が三角形の頂点を通らない直線lとそれぞれP、Q、Rで交わるとき、次の等式が成り立つ。
\(\frac{BP}{PC}⋅\frac{CQ}{QA}⋅\frac{AR}{RB}=1\)



チェバの定理
△ABCの頂点A、B、Cと、この三角形の辺上にもその延長上にもない点Oを結ぶ各直線が、対辺またはその延長とそれぞれ点P、Q、Rで交わるとき、次の等式が成り立つ。
\(\frac{AR}{RB}⋅\frac{BP}{PC}⋅\frac{CQ}{QA}=1\)
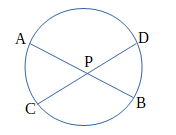
方べきの定理
①点Pを通る2直線が、与えられた円と2点A、Bおよび、2点C、Dで交わるとき、次の等式が成り立つ。
\(PA×PB=PC×PD\)
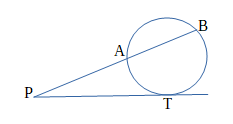
➁円の外部の点Pから円に引いた接線の接点をTとする。Tを通り、この円と2点A、Bで交わる直線を引くとき、次の等式が成り立つ。
\(PA×PB=PT^2\)
よくある例題
図形の性質についての例題をいくつか紹介していきます。
例題 (内分・外分)
線分ABに対して、次の点を図示せよ。
①2:1に内分する点P
②1:4に外分する点Q
解答
内分はAP:PB=2:1、外分はAQ:QB=1:4となればよいので、下の図のようになる。

例題 (外心)
図において、点Oは△ABCの外心である。角度α、βを求めよ。
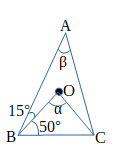
解答
点Oは外心であるので∠OBC = ∠OCB、
また、△OBCについて、∠OBC + ∠OCB + ∠BOC =180°なので
50° + 50° + α = 180°
よって、α = 80°
また、点Oは△ABCの外心であるため、△OAB、△OBC、△OCAは全て二等辺三角形であるので、
15° + 15° + 50° + 50° + 2∠OAC =180°
よって、β = ∠OAB + ∠ OAC = 15° + 25° = 40°
例題 (内心)
図において、点Iは△ABCの内心である。角度αを求めよ。
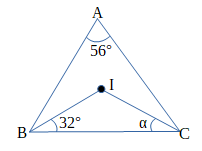
点Iは△ABCの内心であるので、
∠IBA = ∠IBC = 32°
∠ICA = ∠ICB = α
よって、
32° + 32° + 56° + 2α =180°
よって、α = 60° ÷ 2 = 30°
例題 (重心)
図において、点Gは△ABCの重心である。線分の長さx、yを求めよ。
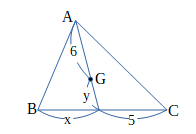
解答
点Gは△ABCの重心であるので、
x = 5
AG : y = 2 : 1
よって、
y = 6 ÷ 2 = 3


例題 (メネラウスの定理)
図において、線分の長さxを求めよ。
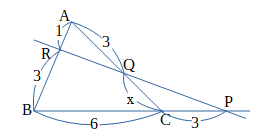
解答
右の図において、メネラウスの定理より、
\(\frac{BP}{PC}⋅\frac{CQ}{QA}⋅{AR}{RB}=1\)
\(\frac{(6+3)}{3}⋅\frac{x}{3}⋅\frac{1}{3}=1\)
よって、x = 3
例題 (チェバの定理)
図において、線分の長さxを求めよ。
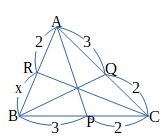
解答
右の図において、チェバの定理より、
\(\frac{BP}{PC}⋅\frac{CQ}{QA}⋅\frac{AR}{RB}=1\)
\(\frac{3}{2}⋅\frac{2}{3}⋅\frac{2}{x}=1\)
よって、\(x = 2\)
例題 (方べきの定理)
図において、線分の長さxを求めよ。
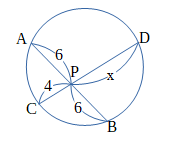
解答
右の図において、方べきの定理より、
\(PA⋅PB=PC⋅PD\)
\(6⋅6=4⋅x\)
よって、\(x = 9\)
図形の性質攻略法
この単元では、内分、外分、内心、外心、重心など、主に三角形や円についての重要な性質がたくさん出てきます。性質、定理ともにたくさんの種類がありますが、この単元の問題は公式や性質をそのまま使うことが多いので、テストのときは公式をしっかりと覚えましょう。また、内分、外分、内心、外心、重心などは図形を扱う単元でよく使うのでしっかりと理解するようにしましょう。
”やる気”と”自信”を育てる、あすなろ関西の学習サポート
どんな単元もコツをつかめば驚くほどスムーズに理解できるようになります! だからこそ、一人で悩み続ける必要はありません。
あすなろ関西は、「やる気づくり」や「できる喜び」を一番に考え、得意な教科から指導することで自信を持ってもらうことを重視しています。
まずはその第一歩として、自宅でもオンラインでも受けられる無料体験授業を、ぜひお気軽にお試しください!