数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。今回は高校数学の中でも数Ⅲの積分について書いていきたいと思います。微分法と同じく数Ⅱで学習した「積分の考え」の内容を発展させた内容になっています。積分を使うと球体のような曲面の面積、体積を求めることができるようになります。計算も式が長くなることが多いので計算ミスに気を付けましょう。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
不定積分と定積分
数Ⅱで学んだ「積分の考え」の発展で、この単元では三角関数、対数関数、指数関数などの関数に対しても積分計算を行っていきます。また、数Ⅱで学んだように積分には定積分と不定積分があります。簡単にいうと、不定積分は積分区間を定めず微分の逆の計算をするだけで、定積分は積分区間を定めて実際にその区間での値を計算します。
積分とその基本的な性質
積分の基本的な考え方は、「微分の逆」です。式を使って表すと、
\( (A)’ = B \) のとき、\( \displaystyle \int B dx = A + C \) (Cは積分定数)
という計算が積分です。上の式からわかるように微分したものを積分すると元に戻るというイメージです。数Ⅱで出てきた積分の基本的な性質を復習すると、
\(
\displaystyle \int kf(x) dx = k \int f(x) dx \\
\displaystyle \int \{ f(x) + g(x) \} dx = \int f(x) dx + \int g(x) dx \\
\displaystyle \int \{ kf(x) + lg(x) \} dx = k \int f(x) dx + l \int g(x) dx
\)
ただ、気を付けなければならないのが、不定積分をしたときは計算した最後に積分定数を加える必要があります。この積分定数は微分すると0になる定数なので積分した関数を微分すると元の関数に戻ります。
置換積分法・部分積分法
まず、置換積分の手順はほほ1パターンしかありません。置換積分では何を置換するかが一番大切なポイントです。置換積分の計算問題では、どのように置換すればいいかわからなくてもとりあえず置換してみて計算するようにしましょう。また、定積分で置換積分を使う場合は、積分区間も変わることに気を付けなければいけません。
部分積分は公式があって、その公式を使って計算問題が解けるように練習問題をこなしていく必要があります。
不定積分の部分積分の公式は、
\(
\displaystyle \int f(x) g'(x) dx = f(x) g(x) – \int f'(x) g(x) dx
\)
また、定積分の公式は、
\(
\displaystyle \int_a^b f(x) g'(x) dx = [ f(x) g(x) ]_a^b – \int_a^b f'(x) g(x) dx
\)
まずはこの公式を見ながら練習問題を解いていき、部分積分の計算方法を身につけましょう。
いろいろな関数の積分
微分法では三角関数、対数関数、指数関数などの微分を学んだと思います。積分法でも三角関数、対数関数、指数関数などの積分計算をしていきます。積分でよく使う公式をまずは覚えていきましょう。
\(
\displaystyle \int ax^{a-1} dx =x^a \\
\displaystyle \int cos x dx = sin x \\
\displaystyle \int (-sin x) dx = cos x \\
\displaystyle \int e^x dx = e^x \\
\displaystyle \int \frac{1}{x} dx = log |x|
\)
これらの関数の積分の計算を身につけ、積分の対象となる関数の範囲を広げ、置換積分法や部分積分法の計算方法も身につけ、複雑な関数の積分も計算していかなくてはいけません。また、分数関数の積分を行なう場合は部分分数分解をし、いくつかの項に分けて積分を行なうといった流れになります。
積分の応用
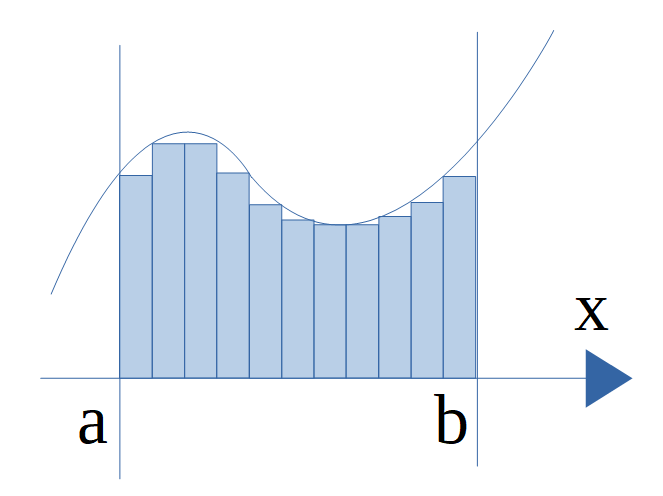
積分の計算を使って、与えられた図形の面積を求めることを区分求積法といいます。この方法は曲線で囲まれた面積は、限りなく細くした\(n\)個の長方形の和で表せるという考え方です。
\(
\displaystyle \Delta x = \frac{b-a}{n} , x_k = a + k \Delta x \\
\displaystyle \lim_{n \to \infty} \sum_{k=1}^n f(x_k) \Delta x = \int_a^b f(x) dx
\)
積分の応用ではこの区分求積法を使って図形面積を求めていきます。
面積、体積、曲線の長さ
面積
数Ⅱで学んだように、積分を使うと面積を求めることができます。区間\( [a , b] \) で常に \( f(x) \ge g(x) \) のとき、曲線 \( y=f(x) , y=g(x) \) と\(x\)軸と2直線 \( x=a , x=b \) で囲まれた部分の面積\(S\)は、
\(
\displaystyle S = \int_a^b \{ f(x) – g(x) \} dx
\)
と表すことができます。基本的にはこの公式でほとんど計算できます。しかし、関数の大小関係で積分区間を分けて計算したりと図形によって工夫して計算しなければいけません。
体積
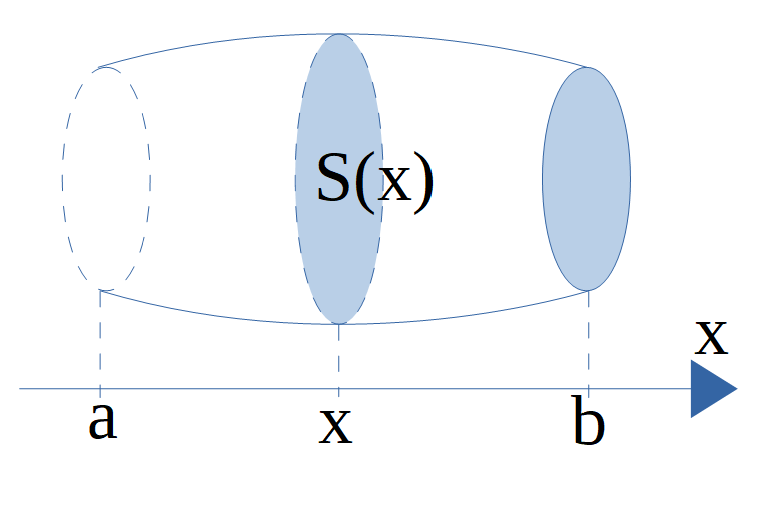
平面図形の面積を区分求積法を使って計算したように、立体図形の体積も区分求積法の考えを利用して定積分で表すことができます。立体図形の体積は断面積を積分して体積を計算するイメージです。\(x\)軸に垂直な2つの平面で挟まれた立体で、この立体の\(x\)軸に垂直な断面積が \( S(x) \) で表されるとすると、この立体の体積\(V\)は、
\(
\displaystyle V = \int_a^b S(x) dx
\)
と表すことができます。
また、\( y = f(x) , x=a , x=b \) 、\(x\)軸で囲まれた部分の回転体の体積は、
\(
\displaystyle V = \pi \int_a^b \{ f(x) \}^2 dx = \pi \int_a^b y^2 dx
\)
と表すことができます。
曲線の長さ
曲線の長さを求める場合は、関数さえ与えられていれば曲線を図示しなくても公式に当てはめて計算すれば求めることができます。曲線の長さを求める公式は根号がついています。計算をしていく過程で根号を外すときは絶対値がつくことに注意しましょう。
\( y=f(x) (a \le x \le b) \) で表される曲線の長さ\(L\)は、
\(
\displaystyle L = \int_a^b \sqrt{ 1+ (\frac{dy}{dx})^2 } dx
\)
媒介変数\(t\)を使った \( x=f(t) , y=g(t) ( \alpha \le t \le \beta) \)で表される曲線の長さ\(L\)は、
\(
\displaystyle L = \int_\alpha^\beta \sqrt{ ( \frac{dx}{dt} )^2+ ( \frac{dy}{dt} )^2 } dt
\)
例題
積分についての例題をいくつか紹介していきます。
例題 (置換積分法)
\( \displaystyle \int (x+2) e^{x^2 + 4x + 1} dx \) を計算せよ。
解答
\( t = x^2 + 4x + 1 \) とおくと、\( dt = ( 2x + 4 ) dx \)
よって、
\begin{eqnarray}
\displaystyle \int (x+2) e^{x^2 + 4x + 1} dx &=& \frac{1}{2} \int (2x+4)e^{x^2 + 4x + 1} dx \\
&=& \frac{1}{2} \int e^{t} dt \\
&=& \frac{1}{2} e^t +C \\
&=& \frac{1}{2} e^{x^2 + 4x + 1} + C
\end{eqnarray}
例題 (部分積分法)
次の積分を計算せよ。
①\( \displaystyle \int x sin x dx \)
②\( \displaystyle \int x e^{2x} dx \)
解答
①
\begin{eqnarray}
\displaystyle \int x sin x dx &=& \int x \cdot (-cos x)’ dx \\
&=& x \cdot (-cos x) – \int 1 \cdot (-cos x) dx \\
&=& -xcos x + \int cos x dx \\
&=& -xcos x -sin x + C
\end{eqnarray}
②
\begin{eqnarray}
\displaystyle \int x e^{2x} dx &=& \int x \cdot ( \frac{1}{2} e^{2x} )’ dx \\
&=& x \cdot ( \frac{1}{2} e^{2x}) – \int 1 \cdot ( \frac{1}{2} e^{2x} ) dx \\
&=& \frac{1}{2} x e^{2x} – \int( \frac{1}{2} e^{2x} ) dx \\
&=& \frac{1}{2} x e^{2x} – \frac{1}{4} e^{2x} + C \\
&=& \frac{1}{4} e^{2x} (2x-1) +C
\end{eqnarray}
例題 (面積)
曲線 \( y = log x \) と原点から曲線に引いた接線と\(x\)軸で囲まれた部分の面積\(S\)を求めよ。
解答
接点の座標を\( (p , log p ) \)とすると、\( y’ = \frac{1}{x} \)より接線の方程式は、
\(
\displaystyle y = \frac{1}{p} x + log p -1
\)
と表せる。この直線は原点を通るので、\( (0 , 0) \)を代入すると、
\( p=e \)
よって、接線の方程式は\( y = \frac{1}{e} x \)、接点は\( (e , 1) \)
また、曲線\( y = log x \) と\(x\)軸との交点は\((1 , 0) \)
よって求める面積\(S\)は、
\begin{eqnarray}
\displaystyle S
&=& \int_0^e \frac{1}{e} x dx – \int_1^e log x dx \\
&=& [ \frac{1}{e} x^2]_0^e – [x log x – x ]_1 ^e \\
&=& \frac{1}{2} e – \{ (e – e ) – ( -1 ) \} \\
&=& \frac{e}{2} – 1
\end{eqnarray}
例題 (曲線の長さ)
曲線\(y = \frac{1}{3} x^3 + \frac{1}{4x} \)の\( 1 \le x \le 2 \)の範囲の長さを求めよ。
解答
曲線の長さを求める公式に当てはめて計算していきましょう。
\begin{eqnarray}
\displaystyle L &=& \int_1^2 \sqrt{ 1+ (\frac{dy}{dx})^2 } dx \\
&=& \int_1^2 \sqrt{ 1+ (x^2 – \frac{1}{4x^2})^2 } dx \\
&=& \int_1^2 \sqrt{ (x^2 + \frac{1}{4x^2})^2 } dx
\end{eqnarray}
積分範囲\(1 \le x \le 2 \)なので\( (x^2 + \frac{1}{4x^2}) \ge 0 \)
よって、
\begin{eqnarray}
\displaystyle L &=& \int_1^2 \sqrt{ 1+ (\frac{dy}{dx})^2 } dx \\
&=& \int_1^2 (x^2 + \frac{1}{4x^2} dx \\
&=& [ \frac{1}{3} x^3 – \frac{1}{4x^2}]_1^2 \\
&=& \frac{59}{24}
\end{eqnarray}
積分攻略法
微分の計算は積・商・合成関数の微分法を身につければほとんどの関数の導関数を求めることができましたが、積分の計算はそれぞれの積分計算ごとに適切な式変形や解法が必要になってきます。ここでは、置換積分法や部分積分法などの積分の計算方法と三角関数などの様々な関数の積分公式を学びます。これらの計算法と公式を使うことで、複雑な図形の面積、体積、曲線の長さなどを求めることができます。積分によって面積、体積、曲線の長さが求められるようになればこの単元で点が取れます。しかし、積分の式を立てることができても計算ができないと点が取れず、複雑な図形ほど計算も複雑になるので公式を覚えたら練習問題をたくさん解くようにしましょう。