こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は\(y=ax^{2}\)という形の関数について学習したいと思います。
これは今まで勉強してきた関数とは少し違った面白い性質があります。何か形が難しそう…と思って気負う必要はありません!一次関数が分かれば大丈夫です。
では、頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
\(y=ax^{2}\)ってなに?
\(y=ax^{2}\)とは、\(x\)を2乗した数に\(a\)を掛けた数が\(y\)になる関数のことです。
今までの\(y=ax\)では、\(x\)の値が1つ増えた時の\(y\)の増える量は一定でした。ところが、\(y=ax^{2}\)という式になると、\(x\)がどの値の時に1増えるか、によって、\(y\)の増える量が変わります。
「こんなヘンテコな関数、いったいどこで使われるの?」と思うかもしれませんが、実際様々なところで使うことができます!
底面が正方形である直方体の体積を求められる!
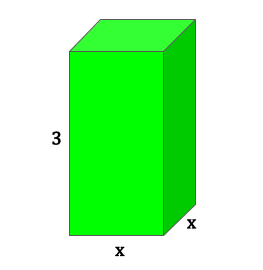
上のように、2辺の長さ(縦と横)が\(x\)、もう1辺の長さ(高さ)が3の立方体の体積\(y\)を考えます。底面の辺が\(x\)なので、底面の形は\(x\)の値によらず正方形となります。
直方体の体積は「縦」×「横」×「高さ」で求めることが出来ますね。今回の場合、縦と横が\(x\)、高さが\(3\)なので、これらを掛け合わせると、\(x×x×3=3x^{2}\)となります。この体積が\(y\)なので、
\(y=3x^{2}\)という式で表せます。
この立方体の体積と底辺の長さ\(x\)の関係を考えてみましょう。
早速、\(x\)に1ずつ数を増やしながら入れてみて、それに対応する\(y\)の値を見てみることにします。
例えば、\(x=1\)のとき、\(1×1×3=3\)となります。同じように値を追加していくと…
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(y\) | \(3\) | \(12\) | \(27\) | \(48\) | \(75\) |
このような表が出来ます。
では、この表から、\(x\)が\(1\)増えた時の\(y\)の値について見てみましょう。
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(y\) | \(3\) | \(12\) | \(27\) | \(48\) | \(75\) |
| \(x\)が1増加した時の\(y\)の増加量 | – | \(9\) | \(15\) | \(21\) | \(27\) |
このように、\(x\)の値が増えていくほど、\(x\)が\(1\)増加したときの\(y\)の増加量が大きくなります。
もう一つ例を考えてみましょう。
斜面を転がるボールの時間と位置を求められる!
次に、斜面を転がるボールの進む距離と時間を考えてみましょう。
ボールを斜面に置いて手を離すと、ボールは時間が経つほど早くなって進んでいきます。(\(y=ax^{2}\)で表すことが出来る数式になります。)
このボールの位置を1秒ごとに写真で撮ってみると、次のようになりました。
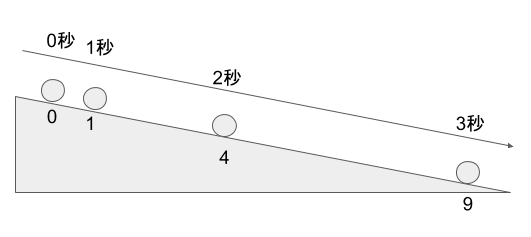
0秒で0、1秒で1、2秒で4、3秒で9の位置にいます。時間を\(x\)、位置を\(y\)として表に表すと、
| 時間\(x\) | 0 | 1 | 2 | 3 |
| 位置\(y\) | 0 | 1 | 4 | 9 |
となります。
このうち、どれか1つの\(x\)、\(y\)のペアを\(y=ax^{2}\)に代入していくと、\(a=1\)であると分かります。例えば、\(x=3\)、\(y=9\)を\(y=ax^{2}\)に代入すると、\(9=9a\)より\(a=1\)とすることが出来ます。
したがって、この関係は\(y=x^{2}\)と示すことが出来ます。
このように、時間や長さに伴って、その値の増え方が一定とならないものでも、\(y=ax^{2}\)という式で表すことが出来る場合があります。
【応用】ものが落ちるときの時間と位置を求められる!
空中でものを落とし始めてからの時間とそのときの位置も、このy=ax^{2}で表すことが出来るんです。(※厳密には少し違います。)
\(y\)を位置、\(x\)を時間、\(a\)を速さが増える力(加速度)を示します。(説明が難しいので単位は省略します。)
これも斜面を転がるボールと同じように、時間が経てば経つほど、どんどん早くなっていくということがわかります。
高校では、この\(a\)を9.8とすることが多く、\(x\)に秒数を入れると、\(x\)秒で\(y\)メートル下に進んだかが分かるんです。詳しくは高校の物理で勉強できるので、興味がある人は、まず\(y=ax^{2}\)をマスターしておきましょう!
まとめ
\(y=ax^{2}\)についてのイメージをつかむことが出来たでしょうか?今回はどんなものかわかってもらえたらそれでOKです!
次からは、\(y=ax^{2}\)のグラフの見方や読み方、具体的な問題等について他のページで解説していこうと思いますので、良かったら読んでみてください!
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。