数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。今回は高校1年生の数学の中でも2次関数について書いていきたいと思います。2次関数は数学はもちろん、物理などでも使うのでしっかりと押さえておきたいですよね。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
2次関数とは
yがxの2次の多項式で表すことのできるとき、yはxの2次関数であるといいます。式で書くと、
\(y={ax}^2+bx+c\)
という形でyをxで表せるもので、2次式で表せるから2次関数なので、上の式でa≠0です。
この単元では、2次関数のグラフについての問題や、条件を与えられて2次関数を求めたり、といったことをします。
2次関数の平行移動・対称移動
2次関数の問題では、式からグラフ、グラフから式を求められなけば解けない問題が多いです。グラフを描く時に、頂点を求めるために平行移動の考え方が必要になってきます。1次関数でも2次関数でも、x軸方向\(p\)に、y軸方向に\(q\)だけ平行移動させる場合、xを\(x-p\)、yを\(y-q\)と書き換えることで求めたい関数が得られます。
また、x軸、y軸、原点に関しての対称移動も使えるようになっておく必要があります。x軸に関して対称移動する場合はグラフで考えると上下が入れ替わる形になるのでyを\(-y\)に、y軸に関して対称移動する場合も同じようにxを\(-x\)に書き換えることで求めたい関数が得られます。原点に関して対称移動する場合は、y軸に関して対称移動した後にx軸に関して対称移動することと同じなのでxを\(-x\)、yを\(-y\)に書き換えることで求めたい関数を得ることができます。
平方完成
平方完成とは2次関数のグラフを描くために2次関数の式を変形することです。2次関数のグラフを描くためには頂点の座標が分からないといけません。\(y={ax}^2+bx+c\)のままではグラフの頂点の座標が分からないので、頂点の座標が分かるように式変形することを平方完成といいます。まず、\(y={ax}^2+bx+c\)を平方完成してみると、
\(y={ax}^2+bx+c\)
\(y=a(x^2+\frac{b}{a}x)+c\)
\(y=a(x^2+2(\frac{b}{2a})x+\frac{b^2}{4a^2 }-\frac{b^2}{4a^2 })+c\)
\(y=a(x^2+2(\frac{b}{2a})x+\frac{b^2}{4a^2})-\frac{b^2}{4a}+c\)
\(y=a(x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a}\)
となります。また、この平方完成された式の頂点は、\((\frac{-b}{2a},\frac{-b^2+4ac}{4a})\)です。2次関数は\(y={ax}^2\)を平行移動させたものという考え方でグラフを描きます。なので頂点の座標を求める必要があり、平方完成を使って頂点を求めます。また、グラフの頂点が分かれば、そこから式を求めることができます。しかし、平方完成は公式が複雑なので、公式自体を覚えるのではなく、式変形のやり方を覚えることをおすすめします。
グラフや座標などの情報から関数を求める
グラフなどの情報から関数を求める場合、基本的には座標を\(y={ax}^2+bx+c\)に代入して、係数\(a、b、c\)を求めることによって、関数を求めます。関数の式を求める問題では、係数などを文字で置き、座標などの情報を代入することによって置いた文字を求めることによって関数を求めていきます。
よくある例題
2次関数についての例題をいくつか紹介していきます。
例題 (グラフを書く)
2次関数\(y=-5x^2+10x-14\)の頂点と軸を求め、グラフを書け。
解答
与えられた2次関数を平方完成すると、
\(y=-5x^2+10x-14\)
\(y=-5(x^2-2x+1-1)-14\)
\(y=-5(x^2-2x+1)+5-14\)
\(y=-5{(x-1)}^2-9\)
よって、頂点は(1, -9)、軸は直線x=1
また、グラフは、以下のようになる。
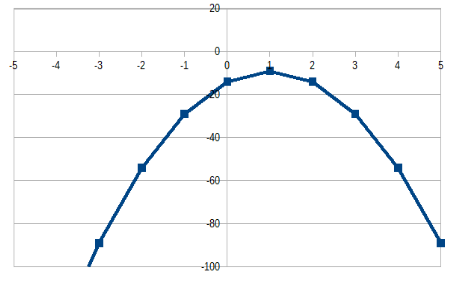
例題 (平行移動・対称移動)
\(y=x^2+2x-5\)のグラフを次のように移動して得られるグラフの2次関数をそれぞれ求めよ。
①x軸方向に-1、y軸方向に3だけ平行移動
②x軸に関して対称移動
③原点に関して対称移動
解答
①x軸方向に-1、y軸方向に3だけ平行移動なので、xに(x+1)、yに(y-3)を代入すれば、求めたい2次関数が求められるので、
\(y-3={(x+1)}^2+2(x+1)-5\)
\(y=x^2+2x+1+2x+2-5+3\)
\(x^2+4x+1\)
よって、\(y=x^2+2x-5\)をx軸方向に-1、y軸方向に3だけ平行移動して得られる2次関数は\(y=x^2+4x+1\)です。
②x軸に関して対称移動するので、yに-yを代入すれば、求めたい2次関数が求められるので、
\(-y=x^2+2x-5\)
\(y=-x^2-2x+5\)
よって、\(y=x^2+2x-5\)をx軸に関して対称移動して得られる2次関数は\(y=-x^2-2x+5\)です。
③原点に関して対称移動するので、yに-y、xに-xを代入すれば、求めたい2次関数が求められるので、
\(-y={(-x)}^2+2(-x)-5\)
\(y=-x^2+2x+5\)
よって、\(y=x^2+2x-5\)を原点に関して対称移動して得られる2次関数は\(y=-x^2+2x+5\)です。
例題 (条件から関数を求める)
3点(-2, -12)、(1, 9)、(3, 3)を通る2次関数を求めよ。
解答
2次関数は\(y={ax}^2+bx+c\)と表すことができるので、3点の座標を代入すると、
\begin{eqnarray} \begin{cases} 12=4a-2b+c & \\ 9=a+b+c
& \\ 3=9a+3b+c& \end{cases} \end{eqnarray}
となります。この連立方程式を解くと係数の\(a、b、c\)を求めることができ、3つ係数\(a、b、c\)を\(y={ax}^2+bx+c\)に代入することによって式を求めることができます。
上の連立方程式を解くと、\(a=-2、b=5、c=6\) となるので、求める2次関数は、
\(y=-2x^2+5x+6\)
と求められます。
苦手克服法
2次関数は数学Ⅰの中でも苦手な人が多いと思います。2次関数では式からグラフを描くことができ、グラフから式が求められることが基本となります。式やグラフのどちらかを与えられて、もう片方がどのようになるかイメージできないという人が多いと思います。2次関数が苦手な人はどんな問題でも、式が与えられたらグラフを、グラフを与えられたら式を求めるようにしましょう。
グラフと式を行き来する
2次関数ではグラフと式を自由に行き来できることが基本になります。これ以降では式とグラフは自由に行き来できることが前提になってくるので平方完成や平行移動はスムーズにできるようになっておくといいですね。