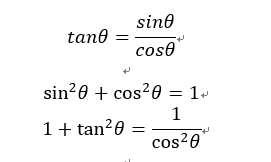数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。今回は高校2年生の数学の中でも三角関数について書いていきたいと思います。三角関数はつまずく人が多い単元なので基礎の部分からじっくりと理解していきたいですね。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
角の拡張
数学Iで学んだ三角比によって、さまざまな図形の辺の長さや角を計算で求めることができるようになりました。三角関数はこの三角比を拡張した単元です。三角関数を学ぶ前の準備として、まずは角度について書いていきたいと思います。
一般角
固定された図形で表される角度の大きさは0°から360°です。
ここでは、これから学ぶ三角関数のために扱う角度を360°以上の角や、回転の向きも考えた角に拡張していきましょう。
360°以上の角を考える場合、動点Pは反時計回りに1周を超えて動いてもいいとします。例えば、動点Pが反時計回りに1周と60°回転していたとすると、\(∠POX = 360° + 60° =420°\)と考えます。
次に負の角について考えていきましょう。動点Pは時計回りに動いてもよいとします。この場合は∠POXを負の値で定めます。例えば、動点Pが時計回りに120°回転していたとすると、\(∠POX = -120°\)と考えます。これらのように360°以上の角や回転の向きも考えた角を一般角といいます。
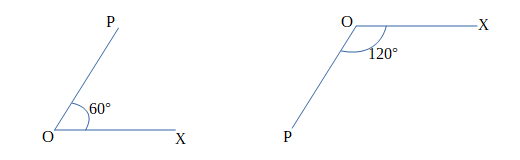
また、一般角θに対して、始めの固定された半直線OXを始線、始線OXから角θだけ回転させた半直線OPを動径といいます。
弧度法
これまで角度を表すのに30°や120°という風に°(度)を使ってきました。この表し方を度数法といいます。今回新しく登場する弧度法では、角度を表すのに扇の弧の長さ、または中心角の大きさの割合を使います。
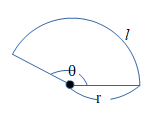
上の図ような円弧において、弧の長さがl、半径がrの中心角θを、
\(θ=\frac{l}{r}\)
と定義します。度数法では[度]という単位を使っていましたが、
弧度法ではラジアンという単位を使います。また、\(r = 1\)の単位円のときを考えると、\(θ=l\)となり、中心角は対応する弧の長さで表されることを意味しています。つまり、\(360° = 2π\) ラジアンです。
三角関数
三角関数とは
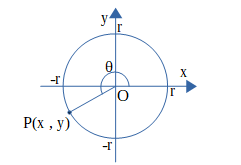
図のようにxy平面において原点Oを中心とした半径rの円を考えます。x軸の正の部分を始線として、角θの動径と円との交点の座標を(x , y)として、一般角θに対する正弦(sin)、余弦(cos)、正接(tan)を
\(sinθ=\frac{y}{r},cosθ=\frac{x}{r},tanθ=\frac{y}{x}\)
と定義します。(ただし、tanθはx = 0となるようなθに対しては定義されない。)
このsinθ 、cosθ 、tanθを角θの三角関数といいます。
三角関数の性質
一般角の三角関数についても、数学Iの三角比と同じような相互関係が成り立ちます。
\(・sin^2 θ+cos^2 θ=1\)
\(・tanθ=\frac{sinθ}{cosθ}\)
\(・1+tan^2 θ=\frac{1}{(cos^2 θ)}\)
三角関数のグラフ
角θの動径と単位円の交点をPとすると、点Pのy座標がsinθになります。よって、関数\(y=sinθ\)のグラフは、
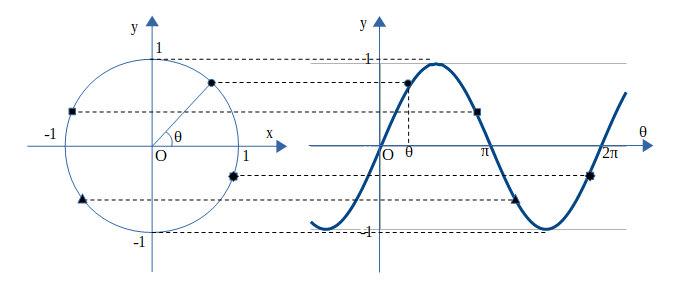
また、\(y=sinθはsin(θ+2π)=sinθ\)から周期\(2π\)の周期関数で、\(-1≤sinθ≤1\)から値域は\(-1≤y≤1\)となります。また、\(sin(-θ)=-sinθ\)から\(y=sinθ\)は原点に関して対称なグラフです。
\(y=cosθ\)や\(y=tanθ\)のグラフも同様にして、描くことができます。
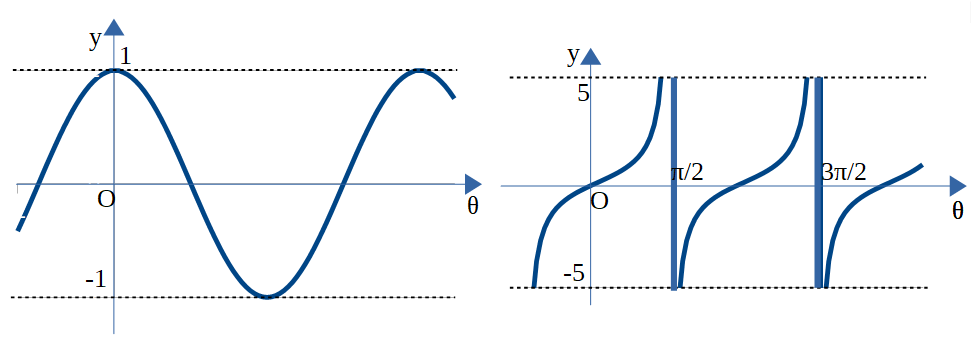
\(y=cosθ\)のグラフを描くときは、角θの動径と単位円の交点をPとすると、点Pのx座標がcosθになります。また、\(y=cosθはcos(θ+2π)=cosθ\)から周期\(2π\)の周期関数で、\(-1≤cosθ≤1\)から値域は\(-1≤y≤1\)となります。また、\(cos(-θ)=cosθ\)から\(y=cosθ\)はy軸に関して対称なグラフです。
\(y=tanθ\)のグラフを描くときは、角θの動径と単位円の交点をPとして、直線OPと直線x=1の交点をQとすると、点Qのy座標がtanθになります。また、\(y=tanθはtan(θ+π)=tanθ\)から周期\(π\)の周期関数で、値域は実数全体となります。また、\(tan(-θ)=tanθ\)から\(y=tanθ\)は原点に関して対称なグラフです。
よくある例題
三角関数についての例題をいくつか紹介していきます。
例題 (弧度法)
次の角を、度数は弧度で、弧度は度数で表せ。
①\(60°\) ②\(\frac{3}{4} π\) ③\(-165°\)
解答
①\(180° = π\)ラジアン であるので
\(60×π/180=π/3\)
よって\(60°\)を弧度法で表すと\(π/3\)
②\(\frac{3}{4} π×\frac{180}{π}=135\)
よって、\(\frac{3}{4} π\)を度数法で表すと\(135°\)
③\(-165×\frac{π}{180}=\frac{11}{12} π\)
よって、\(-165°\)を弧度法で表すと\(\frac{11}{12} π\)
例題 (三角関数のグラフ)
関数\(y=sinθ-1\)のグラフをかき、その周期を求めよ。
解答
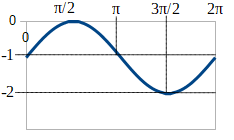
\(y=sinθ-1\)は\(y=sinθ\)をy軸方向に-1だけ平行移動したグラフになるので、上の図のようなグラフになります。
また、周期は2πです。
例題 (三角関数の不等式)
\(0≤θ<2π\)のとき、\(cosθ>\frac{1}{2}\)を解け。
解答
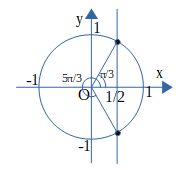
直線\(x=\frac{1}{2}\)と単位円の交点は図のようになり、その角度は\(cosθ=\frac{1}{2}\)より、\(θ=\frac{π}{3},\frac{5}{3} π\)である。よって、図より、\(0≤θ<2π\)で\(cosθ>\frac{1}{2}\)となるのは、\(0≤θ<\frac{π}{3},\frac{5}{3} π<θ<2π\)
三角関数で挫折しないためには
三角関数は数学の中でも昔から難しいといわれている単元です。難しいといわれている単元だからこそ基礎からしっかりと理解していかなければいけません。公式を暗記するのもいいですが、どうしていそうなるのかが大切です。まずは、角度の新しい表し方から、三角関数の方程式、不等式を解くところまで、順を追って理解していくことが大切です。三角関数はグラフを描くことが多いので、単位円でどこなのかイメージがすぐにできるようになるといいと思います。