数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。今回は高校2年生の数学の中でも指数・対数関数について書いていきたいと思います。指数関数や対数関数は日常生活ではなかなか触れる機会がなく、取っ掛かり辛いという人もいると思います。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
わからない…を“わかる!”に変える家庭教師
「勉強がわからない」そんな悩みは、あすなろ関西の家庭教師が解決!一人ひとりに合った勉強方法で、小学生から高校受験までサポート!
たった15分の勉強で、これまでの3倍の効果を実感!そんな効率的な学びを、無料体験で試してみませんか?

=もくじ=
指数関数
指数関数は、名前の通り指数を含んだ関数です。さらに指数関数の単元では、これまで右肩の指数の値が自然数だけだったのを実数に拡張していきます。まずは指数の値が負の数や分数の場合など、指数の拡張からふれていきたいと思います。
指数の拡張
指数法則
\(a^m a^n=a^(m+n)\)
\((a^m)^n=a^{mn}\)
\((ab)^m=a^m b^m\)
指数が整数の場合
まずは指数が負の整数の場合から考えてみましょう。\(3^(-2)\)という数があったとすると、指数法則からこの数を考えると、
\(3^5×3^(-2)=3^(5-2)=3^3\)
\(3^{-2}=\frac{1}{3^2}\)
となります。よって、aを実数、mを自然数とすると
\(a^{-m}=\frac{1}{a^m}\)
指数がゼロの場合
次に指数がゼロの場合を考えていきましょう。\(3^0\)という数を考えましょう。指数が負の整数の場合と同じように指数法則からこの数を考えると、
\(3^5×3^0=3^{5+0}=3^5\)
\(3^0=1\)
となります。よって、実数aのゼロ乗は1になります。
\(a^0=1\)
指数が分数の場合
次は指数が分数の場合です。\(3^{\frac{1}{2}}\)という数があったとすると、指数法則からこの数を考えると、
\((3^{\frac{1}{2}})^2=3^{\frac{1}{2}×2}=3^1\)
この数は2乗すると3になる数なので、3の平方根になります。
\(3^{\frac{1}{2}}=\sqrt{3}\)
また、\(3^{\frac{3}{4}}\)という数を指数法則から考えると、
\((3^{\frac{3}{4}})^4=3^{\frac{3}{4}×4}=3^3\)
この数は4乗すると\(3^3\)になるので、\(3^3\)の4乗根になります。
\((3^{\frac{3}{4}})^4=\sqrt[4]{3^3}\)
よって、aを実数、m、nを整数とすると、
\(a^{\frac{n}{m}}=\sqrt[m]{a^n}\)


指数関数とそのグラフ
指数関数とは、\(a>0,a≠1\)のとき、\(y=a^x\)で表される関数のことです。
\(y=a^x\)のグラフを書くと

\(y=a^x\)のグラフは上のグラフからもわかるように、(0 , 1) , (1 , a)を通り、x軸を漸近線とする曲線になります。上のグラフからa>1のときは増加関数、0<a<1は減少関数になります。また、グラフを平行移動、対称移動する場合は二次関数などと同じように扱うことができます。
\(y=f(x)\)のグラフをx軸方向にp、y軸方向にqだけ平行移動したグラフは\(y-q=f(x-p)\)、x軸に関して対称移動させると\(y=-f(x)\)、y軸に関して対称移動させると\(y=f(-x)\)、原点に関して対称移動させると\(y=-f(-x)\)となります。
対数関数
対数はこの単元で初めて登場します。対数とは簡単にいうと指数の逆です。まずは対数とはどのようなものでどのような性質があるのかから見ていきましょう。
対数
対数とは
\(a>0,a≠1,M>0\)でpが実数のとき、
\(M=a^p⇔log_a M=p\)
と定義します。このときのpをaを底とするMの対数、Mをこの対数の真数といいます。
定義から
\(log_a a^p=p\)
特によく使うのが
\(log_a a=1,log_a 1=0,log_a \frac{1}{a}=-1\)
対数の性質
対数を使っていくときに必ず必要な性質を紹介します。
\(a>0,a≠1,M>0,N>0\)でkが実数のとき、
\(log_a MN=log_a M+log_a N\)
\(log_a \frac{M}{N}=log_a M-log_a N\)
\(log_a \frac{1}{N}=-log_a N\)
\(log_a M^k=klog_a M\)
\(log_a \sqrt[N]{M}=\frac{1}{N} log_a M\)
底の変換公式
対数は底が同じでないと足し算引き算ができないので底の変換公式は必ず覚えましょう。
a , b , cを正の数として、a≠1,b≠1,c≠1のとき、
\(log_a b=\frac{log_c b}{log_c a}\)
対数関数とそのグラフ
対数関数とは、\(a>0,a≠1\)のとき、\(y=log_a x\)で表される関数のことです。
\(y=log_a x\)のグラフを書くと、
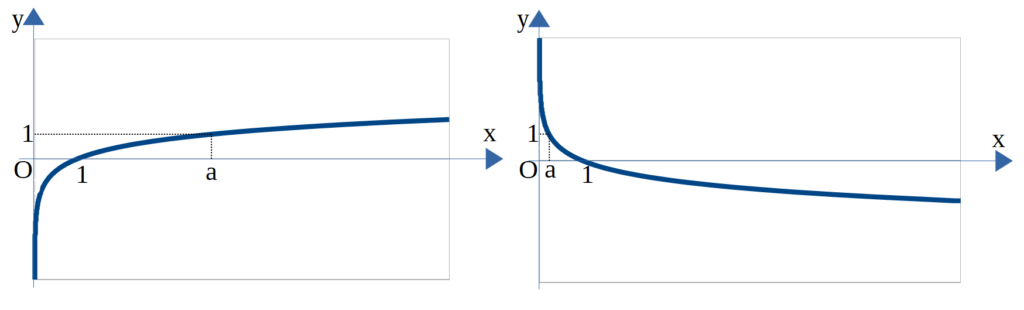
\(y=log_a x\)のグラフは上のグラフからもわかるように、(1 , 0) , (a , 1)を通り、y軸を漸近線とする曲線になります。上のグラフからa>1のときは増加関数、0<a<1は減少関数になります。
\(y=f(x)\)のグラフをx軸方向にp、y軸方向にqだけ平行移動したグラフは\(y-q=f(x-p)\)、x軸に関して対称移動させると\(y=-f(x)\)、y軸に関して対称移動させると\(y=f(-x)\)、原点に関して対称移動させると\(y=-f(-x)\)となります。
よくある例題
指数・対数関数についての例題をいくつか紹介していきます。
例題 (指数関数のグラフ)
関数\(y=2^{x-1}\)のグラフをかけ。
解答
\(f(x)=2^x\)とすると、\(2^(x-1)=f(x-1)\)なので、\(y=2^(x-1)\)のグラフは\(y=2^x\)のグラフをx軸方向に1だけ平行移動したグラフなので、
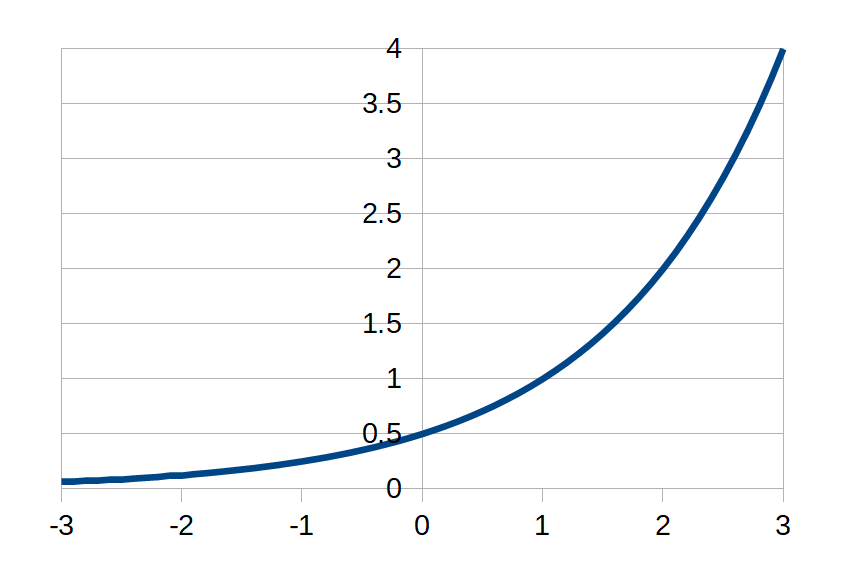
例題 (指数方程式・指数不等式)
次の方程式、不等式を解け。
①\(9^x-2⋅3^x-3=0\) ②\(4^x>\frac{1}{8}\)
解答
①\(9^x\)を\(9^x=(3^x)^2\)と書き直すと、
\((3^x)^2-2⋅3^x-3=0\)
ここで\(3^x=t\)とおくと、
\(t^2-2t-3=0\)
この方程式をtについて解くと、
\(t=-1,3\)
\(3^x=t\)より\(t>0\)なので、
\(t=3\)
\(3^x=t\)から、
\(3^x=3\)
\(x=1\)
②まずは底を2に合わせる。
\(4^x={(2^2)}^x=2^{2x}\)
\(\frac{1}{8}=2^{-3}\)
よって、
\(2^{2x}>2^{-3}\)
底の2は1よりも大きいので、
\(2x>-3\)
\(x>-\frac{3}{2}\)


例題 (対数関数のグラフ)
\(y=-log_{\frac{1}{4}} 4(x+1)^2\)のグラフは\(y=log_2 x\)のグラフをx軸方向にp、y軸方向にqだけ平行移動したグラフである。p、qを求めよ。
解答
底を変換して2つの式の底を合わせる。
底の変換公式を使って、
\(-log_{\frac{1}{4}} 4(x+1)^2\)
\(=-\frac{log_2 4(x+1)^2}{log_2 \frac{1}{4}}\)
\(=-\frac{log_2 4+log_2(x+1)^2}{log_2 2^{-2}}\)
\(=-\frac{2+2log_2 (x+1)}{-2}\)
\(=1+log_2 (x+1)\)
よって、\(y=-log_\frac{1}{4} 4(x+1)^2\)のグラフは、\(y=log_2 x\)のグラフをx軸方向に-1、y軸方向に1だけ平行移動したグラフである。
よって、
\(p=-1,q=1\)
例題 (対数方程式・対数不等式)
次の方程式、不等式を解け。
①\((log_3 x)^2+4log_3 3x=0\) ②\(log_2 (2x-1)>2\)
解答
①真数は正であるので、\(x>0\)
また、\(log_3 3x=log_3 x+log_3 3=log_3 x+1\)から、
\((log_3 x)^2+4log_3 3x\)
\(=(log_3 x)^2+4(log_3 x+1)\)
\(=(log_3 x)^2+4log_3 x+4\)
よって、
\((log_3 x)^2+4log_3 x+4=0\)
\((log_3 x+2)^2=0\)
よって、
\(log_3 x=-2\)
\(log_3 x=-2log_3 3\)
\(log_3 x=log_3 3^{-2}\)
\(log_3 x=log_3 \frac{1}{9}\)
よって、
\(x=\frac{1}{9}\)(\(x>0\)を満たしている)
②真数は正であるので、\(x>\frac{1}{2}\)
与えられた不等式を式変形すると、
\(log_2 (2x-1)>2\)
\(log_2 (2x-1)>log_2 2^2\)
底の2は1よりも大きいので、
\(2x-1>2^2=4\)
これを解いて、
\(x>\frac{5}{2}\)
\(x>\frac{1}{2}\)と\(x>\frac{5}{2}\)の共通部分を考えて、
\(x>\frac{5}{2}\)
指数・対数関数攻略法
指数はこれまで簡単な計算だけ、対数はこの単元で初めて登場しました。この単元で出てくる問題は指数・対数に慣れるまでは複雑に見えるかもしれません。しかし、この単元の問題は「グラフが描ける」ことと「底をそろえる」ことさえできれば解くことができます。 底さえそろえてしまえば簡単な方程式か不等式を解くだけになります。また、指数・対数関数のグラフを描くときには、x軸、y軸との交点、指数関数であればa>0,a≠1のときy=a^xは必ず正、対数関数であれば真数が必ず正になることをおさえておきましょう。特に初めて登場する対数は難しそうに見えますが、「グラフが描ける」ことと「底をそろえる」ことができればそんなに難しくはありません。
”やる気”と”自信”を育てる、あすなろ関西の学習サポート
どんな単元もコツをつかめば驚くほどスムーズに理解できるようになります! だからこそ、一人で悩み続ける必要はありません。
あすなろ関西は、「やる気づくり」や「できる喜び」を一番に考え、得意な教科から指導することで自信を持ってもらうことを重視しています。
まずはその第一歩として、自宅でもオンラインでも受けられる無料体験授業を、ぜひお気軽にお試しください!