数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。今回は高校2年生の数学の中でも微分と積分の考え方について書いていきたいと思います。微分と積分といえば、高校数学最大の難関とも言われていて、めちゃくちゃ難しそうなイメージですよね。逆に言えば、微積分が苦手な人は多いので他の人と差をつけるチャンスです。基礎の考え方の部分から理解して、確実に身につけて点を稼ぎたいですよね。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
わからない…を“わかる!”に変える家庭教師
「勉強がわからない」そんな悩みは、あすなろ関西の家庭教師が解決!一人ひとりに合った勉強方法で、小学生から高校受験までサポート!
たった15分の勉強で、これまでの3倍の効果を実感!そんな効率的な学びを、無料体験で試してみませんか?

=もくじ=
微分の考え
微分とは変数の微小な変化に対する関数の変化の割合のことです。関数\(y=f(x)\)を\(x\)で微分する場合でいうと、\(x\)をほんの少し変化させたときに\(y\)がどれくらい変化するかのことです。
平均変化率・極限
関数\( y=f(x) \) において、\(x\)の値が\(a\)から\(b\)まで変化するとき、\(x\)の変化量は\(b-a\)、\(y\)の変化量は\( f(b) – f(a) \) です。このときの変化の割合(傾き)は、
\(
\displaystyle \frac{f(b)-f(a)}{b-a}
\)
と表すことができ、これを \(x\)の値が\(a\)から\(b\)まで変化するときの平均変化率といいます。
また、関数\( f(x) \)において、\(x\)が\(a\)と異なる値をとりながら限りなく\(a\)に近づくとき\( f(x) \)の値が一定の値\( \alpha \)に近づくことを
\( \displaystyle \lim_{x \to a} f(x) = \alpha \) または \( x \to a \) のとき \( f(x) \to \alpha \)
と表し、\(\alpha\)のことを\(x\)が\(a\)に近づくときの極限値といいます。
関数\( f(x) \)の\(x\)の値が\(a\)から\(b\)まで変化するときの平均変化率において、\(b\)を\(a\)に限りなく近づけたときの平均変化率を関数\( f(x) \) の\( x=a\)における微分係数といい、\(f'(a)\)のように表します。関数\( f(x) \)の\(x\)の値が\(a\)から\(b\)まで変化するときの平均変化率\( \frac{f(b)-f(a)}{b-a} \)において、\( b-a =h\)とおくと、関数\(f(x)\)の\(x=a\)における微分係数\(f'(a)\)は、
\(
\displaystyle f'(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h}
\)
と表される。微分係数\(f'(a)\)は、曲線\(y=f(x)\)上の点\(( a , f(a))\)における接線の傾きです。


「微分する」とは
「微分する」とは、関数\(f(x)\)の導関数\(f'(x)\)を求めることをいいます。関数\(f(x)\)の導関数\(f'(x)\)は、関数\(f(x)\)の\(x\)における微分係数\(f'(x)\)と同じことです。関数\(f(x)\)を\(x\)について微分するときの導関数の定義式は、
\(
\displaystyle f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}
\)
と表されます。
導関数の性質
微分して出てくる導関数の基本的な性質を紹介しておきます。
・\(n\)を自然数とすると、\((x^n)’ = nx^{n-1}\)
・定数\(c\)について、\((c)’=0\)
・\(y=kf(x)\)のとき、\(y’=kf'(x)\)
・\(y=f(x)+g(x)\)のとき、\(y’=f'(x)+g'(x)\)
・\(y=f(x)-g(x)\)のとき、\(y’=f'(x)-g'(x)\)
・\(y=kf(x)+lg(x)\)のとき、\(y’=kf'(x)+lg'(x)\)
(\(k,l\)は定数)
関数の増減、極値
まずはじめに実数\(a , b\)に対して、不等式\(a \le x \le b\) や \(x \ge a\)等を満たす実数\(x\)の値の範囲全体を区間といいます。
ある区間で、常に\(f'(x) > 0 \)ならば関数\(f(x)\)はその区間で増加し、常に\(f'(x) < 0 \)ならば関数\(f(x)\)はその区間で減少します。
また、関数\(f(x)\)において、\(f'(a)=0\)でかつ\(x=a\)の前後で\(f'(x)\)の符号が変わるとき、関数\(f(x)\)は\(x=a\)で極値をとります。
\(f'(a)=0\)で\(x=a\)の前後で\(f'(x)\)が正から負に変わるとき、\(f(x)\)は\(x=0\)で極大であり、\(f(a)\)は極大値です。
\(f'(a)=0\)で\(x=a\)の前後で\(f'(x)\)が負から正に変わるとき、\(f(x)\)は\(x=0\)で極小であり、\(f(a)\)は極小値です。この極大値と極小値を合わせて極値といいます。
積分の考え
積分とは微分の逆の演算のことで、関数の積分は、微分するとになる関数を求めることです。
不定積分
関数\(f(x)\)に対して、微分すると\(f(x)\)になる関数\(F(x)\)を\(f(x)\)の原始関数といいます。また、任意の定数\(C\)を使うと、\( \{F(x)+C\}’=f(x) \)となるため、\(F(x)+C\)は\(f(x)\)の原始関数です。関数\(f(x)\)の任意の原始関数\(F(x)+C\)は
\(
\displaystyle \int f(x) dx
\)
と表し、\(f(x)\)の不定積分といいます。
\(
\displaystyle \int f(x) dx = F(x) + C
\)
このとき、定数\(C\)を積分定数といい、\(f(x)\)の不定積分を求めることを\(f(x)\)を「積分する」といいます。
\(n\)が自然数のとき、導関数は\((x^n)’=nx^{n-1}\)であったので
\(
\displaystyle \int x^n dx = \frac{1}{n+1} x^{n+1} +C
\)
と表すことができます。
不定積分の性質
不定積分の基本的な性質を紹介しておきます。
\(
\displaystyle \int kf(x) dx = k \int f(x) dx \\
\displaystyle \int \{ f(x) + g(x) \} dx = \int f(x) dx + \int g(x) dx \\
\displaystyle \int { kf(x) + lg(x) } dx = k \int f(x) dx + l \int g(x) dx
\)
定積分と面積
関数\(f(x)\)の原始関数\(F(x)\)、2つの実数\(a,b\)に対して、\(F(b)-F(a)\)を関数\(f(x)\)の\(a\)から\(b\)までの定積分といい、
\(
\displaystyle \int_a^b f(x) dx
\)
と表し、このときの\(a\)を下端、\(b\)を上端といいます。この定積分を求めることを、関数\(f(x)\)を\(a\)から\(b\)まで積分するといいます。
\(
\displaystyle \int_a^b f(x) dx = [ F(x) ]_a^b = F(b) – F(a)
\)
また、定積分でも不定積分と同様の性質があるのに加えて、定積分では次のような性質もあります。
\(
\displaystyle \int_a^a f(x) dx = 0 \\
\displaystyle \int_a^b f(x) dx = – \int_b^a f(x) dx \\
\displaystyle \int_a^b f(x) dx = \int_c^b f(x) dx + \int_a^c f(x) dx
\)
2つの曲線の間の面積
定積分を使って関数と関数の間の面積を求めることができます。
区間\(a \le x \le b \)で\( f(x) \ge g(x) \)のとき、2つの曲線\(y=f(x) , y=g(x) \)と2つの直線\( x=a , x=b \)で囲まれた図形の面積\(S\)は、
\(
\displaystyle \int_a^b \{ f(x) – g(x) \} dx
\)
と表すことができます。
例題
微分と積分についての例題をいくつか紹介していきます。
例題 (微分)
次の関数を微分せよ。
①\( y = x^3 – 4x^2 + 6x +24 \)
②\( y = ( x – 1 )( x + 1 )^2 \)
解答
①
\(y = f( x ) + g( x )\)のとき、\(y = f'( x ) + g'( x )\)なので、
\( y’ = (x^3)’ -(4x^2)’ + (6x)’ +(24)’ = 3x^2 – 8x + 6 \)
②
\( y = ( x – 1 )( x + 1 )^2 = ( x^2 -1 )( x + 1 ) = x^3 + x^2 – x – 1 \)
よって、
\( y’ = ( x^3 )’ +( x^2 )’ – ( x )’ – ( 1 )’ = 3x^2 + 2x – 1 \)


例題 (関数の増減、極値)
関数\(y=\frac{1}{3} x^3 – 3 x^2 + 8x -3 \)の増減を調べよ。
解答
与えられた関数をxについて微分すると、
\(y’ = x^2 – 6x + 8 = ( x-4 )( x-2 ) \)
\( y’=0\)とすると、\( x=4,2\)
このとき、yの増減表は次のようになる。
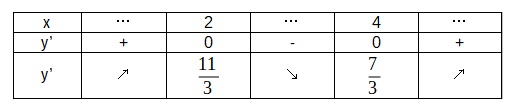
増減表から\(y\)は、
\(x \le 2 , x > 4 \)で増加し、
\( 2 < x \le 4 \)で減少する。
例題 (積分)
次の不定積分、定積分を求めよ。
①\( \displaystyle \int ( 3x^2 + 6x – 2 ) dx \)
②\( \displaystyle \int_{-1}^3 ( x – 1 )( x + 1 ) dx \)
解答
①
\( \displaystyle \int \{ kf( x ) + lg( x ) \} dx = k \int f( x ) dx + l \int g( x ) dx\)から、
\begin{eqnarray}
\displaystyle \int ( 3x^2 + 6x – 2 ) dx &=& 3 \int x^2 dx + 6 \int x dx -2 \int dx \\
&=& 3 \cdot ( \frac{1}{3} x^3 ) + 6 \cdot ( \frac{1}{2} x^2 ) – 2 \cdot x +C \\
&=& x^3 + 3x^2 – 2x +C
\end{eqnarray}
(\(C\)は積分定数)
②
\begin{eqnarray}
\displaystyle \int_{-1}^3 ( x – 1 )( x + 1 ) dx &=& \int_{-1}^3 ( x^2 – 1 ) dx \\
&=& [ \frac{1}{3} x^3 – x ]_{-1}^3 \\
&=& ( 9-3 ) – ( – \frac{1}{3} +1 ) = \frac{16}{3}
\end{eqnarray}
例題 (定積分と面積)
曲線\(y=x^2 – 5x+4 \)と\(x\)軸で囲まれた図形の面積\(S\)を求めよ。
解答
\(x^2 – 5x+4 =(x-1)(x-4) \)より、\(y=x^2 – 5x+4 \)は\(x=1,4\)で\(x\)軸と交わり、\(1 \le x \le 4 \)で\(y \le 0 \)なので、求める面積\(S\)は、
\begin{eqnarray}
\displaystyle S &=& – \int_1^4 (x^2 – 5x +4) dx \\
&=& -[ \frac{1}{3} x^3 – \frac{5}{2} x^2 +4x ]_1^4 \\
&=& -( \frac{64}{3} – 40 +16 ) + ( \frac{1}{3} – \frac{5}{2} + 4 ) \\
&=& \frac{9}{2}
\end{eqnarray}
微分・積分の考え攻略法
微分・積分は高校数学最大の難関といわれていますが、数学Ⅱの微分・積分は基礎の部分だなので出てくるのは定義や考え方、計算方法だけです。計算もそんなに難しくないので、計算の仕方と公式だけ覚えてしまえば解ける問題がほとんどだと思います。微分は傾きを求めていて、増減表を書くことができればOKです。積分で求めているのは面積でグラフのどこの部分を求めているのかイメージできると応用問題等にも対応できると思います。微分・積分で本当に難しいのは数学Ⅲの内容なので数学Ⅱの「微分・積分の基礎」はそんなに恐れずに考え方や定義からおさえていきましょう。
”やる気”と”自信”を育てる、あすなろ関西の学習サポート
どんな単元もコツをつかめば驚くほどスムーズに理解できるようになります! だからこそ、一人で悩み続ける必要はありません。
あすなろ関西は、「やる気づくり」や「できる喜び」を一番に考え、得意な教科から指導することで自信を持ってもらうことを重視しています。
まずはその第一歩として、自宅でもオンラインでも受けられる無料体験授業を、ぜひお気軽にお試しください!