数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。今回は高校2年生の数学の中でも確率分布と統計的な推測について書いていきたいと思います。確率は高校1年のときに数学Aで学んだと思いますが今回の内容はその続きです。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて高校生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
確率分布
確率変数と確率分布
確率変数とは、試行の結果によって、その値をとる確率が定まる変数のことです。確率変数とその値をとる確率との対応を示したものを確率分布といいます。確率変数\(X\)の値を\( x_1 , x_2 , \cdots , x_n \)として、それぞれに対応する確率を\( p_1 , p_2 , \cdots , p_n \)とすると、
\(
p_1 \ge 0 , p_2 \ge 0 , \cdots , p_n \ge 0 \\
p_1 + p_2 + \cdots + p_n = 1
\)
といった確率\(P\)に関することが成り立ちます。また、確率変数\(X\)の確率分布は以下のような表で表されます。
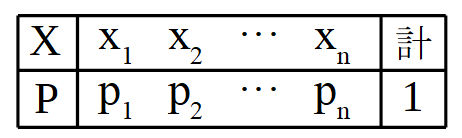
このとき、確率変数\(X\)の値が\(a\)となる確率を\(P(X=a)\)と表し、\(X\)が\(a\)以上\(b\)以下の値となる確率は\(P( a \le X \le b )\)と表します。
この確率分布の特徴を表すのに、確率変数の平均（期待値）、分散、標準偏差というものがあります。これらは、平均値→分散→標準偏差 の順で求めることができます。
確率変数\(X\)の確率分布が上の表のように与えられたとき、
\(x_ 1 p_1 + x_2 p_2 + \cdots + x_n p_n\)
を確率変数\(X\)の平均、または期待値といい、\(E(X)\)で表します。
\( \displaystyle E( X ) = x_1 p_1 + x_2 p_2 + \cdots + x_n p_n = \sum _{i=1}^{n} x_i p_i\)
この確率変数\(X\)の平均を\(m\)とすると、分散\(V(X)\)は以下のような式で表すことができます。
\( \displaystyle V( X ) = E((X – m)^2) = ( x_1 – m )^2 p_1 + ( x_2 – m )^2 p_2 + \cdots + ( x_n – m )^2 p_n\)
そして、標準偏差\(\sigma(X)\)は分散の正の平方根で表されます。
\(\sigma(X) = \sqrt{V(X)}\)
二項分布
1回の試行で事象\(A\)の起こる確率が\(p\)、起こらない確率が\(q\)のとき、この試行を\(n\)回行ったときに事象\(A\)が起こる回数を\(X=k\)回とするとき、\(X\)は確率変数となり、確率\(P\)と確率分布表は、
\begin{eqnarray}
\displaystyle P( X = k ) = {}_n C_k p^k q^{ n-k }
\end{eqnarray}
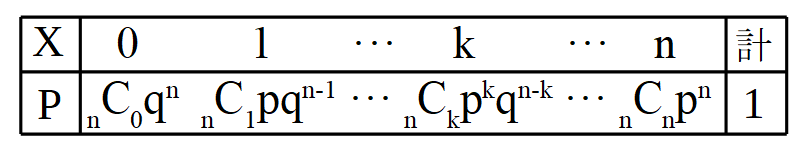
と表すことができます。この表の確率\(P\)をすべて足し合わせたものは二項定理の展開式になっていることから、このような確率分布を二項分布といい、\(B(n,p)\)で表されます。
正規分布
確率変数\(X\)が連続的な値をとり、\(\alpha \le X \le \beta \)の範囲にある確率\(P( \alpha \le X \beta ) \)が下の図の斜線部の面積で表されるとき、関数\(y=f(x)\)を\(X\)の確率密度関数といいます。確率密度関数は全区間で積分すると1になるという性質があります。
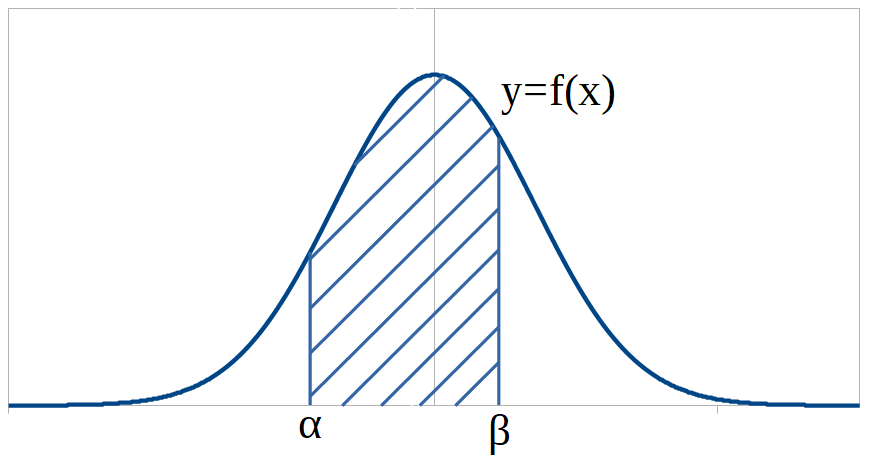
統計において一番よく出てくるのが正規分布（ガウス分布）です。特に、平均が0、標準偏差が1となる正規分布を標準正規分布といいます。平均\(m\)、標準偏差\(\sigma\)の正規分布は以下のような関数で表すことができます。
\(
\displaystyle f(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{- \frac{(x-m)^2}{2 \sigma^2}}
\)
このとき確率変数\(X\)は正規分布\(N( m , \sigma^2 )\)に従うといいます。また、この式から平均\(m\)の値によって、左右にグラフを平行移動させることができ、標準偏差\(\sigma\)の値によってグラフの幅を変えることができます。
また、標準正規分布は以下の関数で表すことができます。
\(
\displaystyle f(z) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{z^2}{2}}
\)
正規分布を使う問題では標準正規分布の表を使うため、正規分布を標準正規分布へ標準化する必要があります。変数\(X\)が平均\(m\)、標準偏差\(\sigma\)の正規分布に従うとき、
\(
\displaystyle Z = \frac{X-m}{\sigma} \Leftrightarrow X = m + Z \sigma
\)
と変換すると、\(Z\)は標準正規分布になります。
また、この正規分布は、
・平均値と最頻値と中央値が一致する。
・平均値を中心にして左右対称である。
・x軸が漸近線である。
といった性質があり、問題で使うこともあるので覚えておきましょう。
統計的な推測
母集団と標本
調査の対象全体から一部を抜き出して調べ、それから全体を推測することを標本調査といいます。標本調査をするときに調べようとする調査の対象全体のことを母集団といい、調査のために母集団から抜き出された要素の全体を標本といいます。標本を抜き出すことを抽出といい、標本に含まれる要素の個数を標本の大きさといいます。標本調査によって正確な推測をするためには、標本に偏りのでないように公平な抽出を行なう必要があります。標本の大きさが十分に大きいとき、その標本の平均は近似的に正規分布\(N(\mu , \frac{\sigma^2}{n})\)に従います。また、母集団が正規分布のとき、\(n\)の大きさにかかわらず、標本の平均は正規分布\(N(\mu , \frac{\sigma^2}{n})\)に従います。
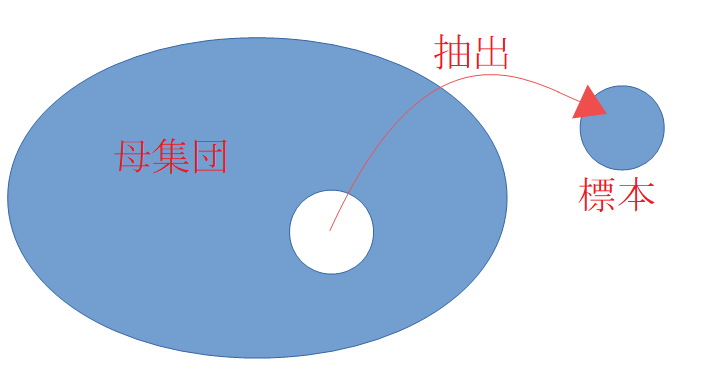
推定
母集団の分布が持っている定数の値が未知のときに、与えられたと標本からその値を推測する方法を推定といいます。母集団の特性を推定するときには、標本から得られた量ににある幅を取って考えます。これを区間推定といいます。
例題
確率分布と統計的な推測についての例題をいくつか紹介していきます。
例題 (確率分布)
1つのサイコロを投げるとき、出る目の分散と標準偏差を求めなさい。
解答
まず、平均（期待値）を求めると、
\( \displaystyle m=(1+2+3+4+5+6) \cdot \frac{1}{6} = \frac{7}{2}\)
次に分散を求めると、
\begin{eqnarray}
V &=& \{( 1- \frac{7}{2} )^2 + (2- \frac{7}{2} )^2 + ( 3- \frac{7}{2} )^2 + ( 4- \frac{7}{2} )^2 + ( 5 – \frac{7}{2} )^2 + ( 6- \frac{7}{2} )^2 \} \cdot \frac{1}{6} \\
&=& \frac{1}{4} \cdot ( 25 + 9 + 1 + 1 + 9 + 25 ) \cdot \frac{1}{6} \\
&=& \frac{35}{12}
\end{eqnarray}
よって標準偏差は、
\(
\displaystyle \sigma = \sqrt{V} = \sqrt{\frac{35}{12}} = \frac{\sqrt{105}}{6}
\)
よって、分散は\( \displaystyle \frac{35}{12}\)、標準偏差は\( \displaystyle \frac{\sqrt{105}}{6}\)
例題 (正規分布)
確率変数\(X\)が正規分布\(N(10,5^2)\)に従うとき、\(5<X<25\)となる確率を求めよ。
解答
\(5=m+Z\sigma , 25 = m+Z\sigma\)より、
\( \displaystyle \frac{5-10}{5} = -1 , \frac{25-10}{5} = 3\)
よって、
\(
P(5<X<25)=P(-1<Z<3)=0.4987+0.3413=0.8400
\)
例題 (統計的な推測)
標準偏差25.5の母集団から、100個の標本を足りだして調べるとその平均は55.0であった。母集団の平均の信頼度95％での信頼区間を求めよ。ただし、100は十分に大きい数とする。
解答
標本の大きさは十分に大きいのでこの標本の平均は正規分布\(N(\mu , \frac{\sigma^2}{n})\)に従います。正規分布表に載っているのは標準正規分布で\(N(0,1)\)なので求めたい\(N(\mu , \frac{25.5^2}{100})\)を標準化する。
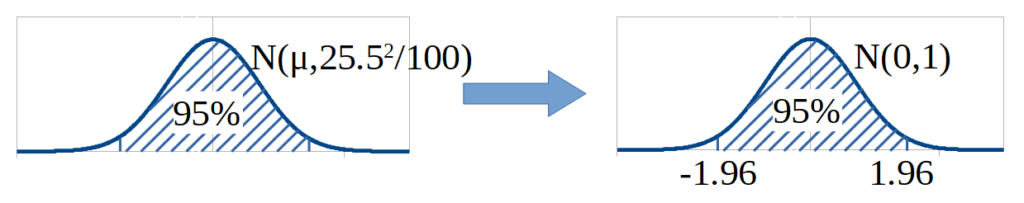
正規分布と標準正規分布の関数を比較すると変換後の標準化された確率変数\(Z\)は、
\( \displaystyle Z = \frac{X-m}{\sigma} \)
と表すことができる。
正規分布の表は0よりも右の面積なので、信頼度95%より面積は0.95であり、この半分の0.475を正規分布の表から探すと、Z=1.96であることがわかる。このとき、標準化された後の平均\( Z = \frac{X-m}{\sigma} \)は-1.96から1.96の範囲に入っていなければならないので、
\(
\displaystyle -1.96 \le \frac{ 55 – \mu }{2.55} \le 1.96
\)
を満たす。この不等式を解くと、
\(
\displaystyle 50.002 \le \mu \le 59.998
\)
よって信頼区間は\(\displaystyle 50.002 \le \mu \le 59.998 \)
確率分布と統計的な推測を勉強するメリット
大学入試であまり使われないため学校によってはいい加減に扱われがちですが、この単元の問題はワンパターンなので数学が苦手な人でも点が取りやすいです。平均や分散、標準偏差の求め方と標準正規分布の使い方がわかればかなり多くの問題を解くことができます、また、もし数Bが選択問題だった場合、確率分布・統計を選択すればベクトルや数列の片方を選択しなくてもよくなるので、苦手な人は確率分布・統計を使って点数アップを狙いましょう。
