こんにちは。あすなろスタッフのカワイです。
今回は、乗法と加法で使える交換法則と結合法則について解説していきたいと思います。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
計算法則その1 交換法則
加法・乗法にも小学校で習った足し算・掛け算と同じように計算法則があります!1つ目は交換法則です。
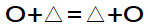
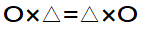
交換法則とは、項を入れ替えても計算結果は同じになるというものです。
例を挙げていきます。
まず、\(17+(-29)\)という式があったときに、交換法則により
\((-29)+17\)
と書き換えることが可能です。どちらの和も-12となるので、正しいということが分かって頂けると思います。
これは、乗法の例です。
\(2×(-3)=(-3)×2\)
交換法則により、上のように表すことが可能です。
減法や除法では使えない
ちなみに、減法(引き算)や除法(割り算)についてはこの法則を満たしません。
たとえば、\((-3)-5\)という式があったときに、交換法則が仮に成り立つとすれば\((-3)-5=5-(-3)\)となるはずですが、
左辺は\((-3)-5=-8\)
右辺は\(5-(-3)=8\)
となるので、答えの符号が異なってしまいます。
除法についても、\(4÷3=3÷4\)とはなりません。
加法・乗法で使える交換法則を間違えて減法・除法に使わないように注意しましょう。
計算法則その2 結合法則
加法・乗法で使うことができる2つ目の計算法則は結合法則です。
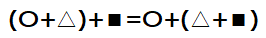
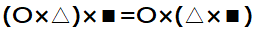
結合法則とは、計算する順番が違っても計算結果は同じになるという法則です。上の式から説明すると、〇と△を足し合わせてから■と足し合わせるのと、△と■を足し合わせてから〇と足し合わせるのでは、計算結果は同じという事です。
1つ目の法則は正直どこで使うの?という法則ではありましたが、この法則は知っていると計算を容易にすることができます。
たとえば
\(15×5×4\)
という式があったとします。
この計算、先に\(15×5\)を先に計算すると、
\(75×4\)
となり、暗算するには少々面倒な数字が出てきてしまいます。
一方、結合法則より計算順序を変えて5×4から先に計算することにします。すると、
\(15×20\)
となります。1つの項の1桁目が0になったので、計算しやすい形となりました。
答えはどちらも\(300\)となります。
減法・除法では使えない
こちらの法則も減法・除法で使うことが出来ません。
たとえば\(24÷6÷4\)という式があったときに、左から順番に計算していくと
\(24÷6÷4=4÷4=1\)
となります。一方\(24÷(6÷4)\)を先に計算すると、
\(24÷(6÷4)=24÷1.5=16\)
となります。
減法についても確認していきましょう。
\(24-12-8\)という式があったときに、これをそのまま前から計算すると、
\(24-12-8=12-8=4\)
となります。一方で、\(24-(12-8)\) とすると、
\(24-(12-8)=24-4=20\)
となります。
このように、減法や除法では計算する順序が変わると、その答えも変わってしまうので、結合法則を用いることが出来ないというわけです。
まとめ
交換法則・結合法則によって、項の順番を自由に変えることができ、自由な順番で計算ができます。これらの法則は計算のなかでも最も大事な原則となるので、必ず覚えておくようにしましょう。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。