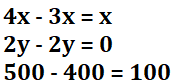こんにちは!あすなろスタッフのカワイです!
今回は、単項式同士の乗法・除法についてお話していきます!
そもそも単項式とは何だったかというと…
字や記号が掛け合わされて1つの項として表されたもののことですね!多項式は、それらが+、-で繋がれて複数の項で成り立っているもののことを言うのでした。
今回はその単項式同士の掛け算や割り算をしていきたいと思います!
文字と数字の並びかえについて覚えていないという方についても、わかりやすくおさらい出来るので、ぜひ最後まで読んでみてください!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
文字と数字の計算ルールのおさらい
単項式の乗法・除法を勉強していく前に、”文字と数字が混ざった計算って、どうやってやればいいのか忘れちゃった…”という人のために、少し復習していきましょう!
- 数字と文字が混ざった式は、答えが文字と数字の積で表される
数字と文字の混ざった計算の場合、その答えは”数字のみの形”や”文字のみの形”ではなく、数字と文字の積の形になります。文字や数字でまとまった後、それ以上計算することができません。
例:\(6×a=6a\) ←これ以上まとめることができない!
- 数字同士・同じ文字同士で計算する
数字×数字などは今まで勉強してきた通り行いますが、文字の計算は同じ文字同士でないと計算することができません。
例:\(a×a\)は同じ文字なので、\(a^{2}\)とすることができます
\(a×b\)は別の文字なので、\(×\)を外して\(ab\)とすることしかできません。
- 並び順は、数字→文字(アルファベット順)
答えの文字の並び順は、数字が最初、その後に文字がアルファベット順、となります。
例:\(c×3×a×z=3acz\)
では、これらのルールを踏まえて、例題に取り組んでいきましょう!
(より詳しく文字と数字の並びルールについて復習したい方はこちら:
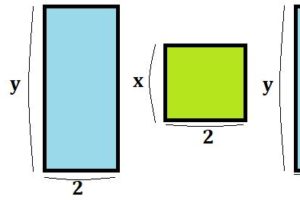
単項式の乗法その①:長方形の面積
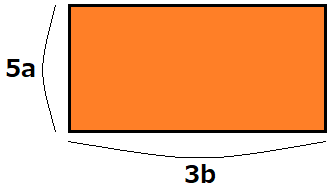
上の図のようなたてが\(5a\)、よこが\(3b\)の長方形があります。この面積を求めたいのですが、さて、どのように計算したら良いでしょうか?
小学校の頃の記憶を引き出してみると、長方形の面積の求め方は「たて×よこ」で求められましたね!
仮に、たてが\(5\)、よこが\(3\)だとしたら、\(5×3\)で答えは\(15\)です!
ただ、今回の問題には文字が入っています。どのように計算していくのか見ていきましょう!
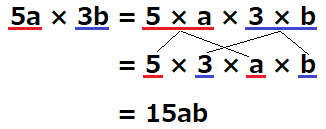
解き方
- まず、単項式の数字と文字を全て分解して、×でつなぐ形にします。
- 次に、数字は数字、文字は文字、といった形で並べ替えをします。この時、数字が先、文字が後になるようにしましょう
- 数字同士、文字同士で計算をします。 今回の場合、数字の\(5×3\)は\(15\)、文字の\(a×b\)はそのまま\(ab\)となります。それを最終的に単項式の形にするので、答えは\(15ab\)となります!
どうでしょうか?途中式を見るとややこしそうに感じるかもしれませんが、答えは意外とあっさりとしたものです。
重要な事は、【数字同士、文字同士で計算する】というところにあります!それさえ理解できれば、途中式を省略して答えを導いてしまっても構いません!(テストなどで途中式を書くように指示があった場合は、省略せずに書いてくださいね!)
確認の為、もう1つ例題を見て解いてもらいましょう!
単項式の乗法その②:直方体の体積
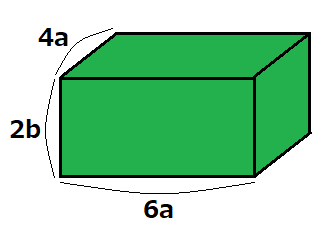
次は、上のような直方体の体積を求めていきましょう。
直方体の体積は「たて×よこ×高さ」で求められると小学校で学習しましたね!前の例題とは、高さの要素が加わったところが違うだけなので、同じように計算をすることが出来ます!
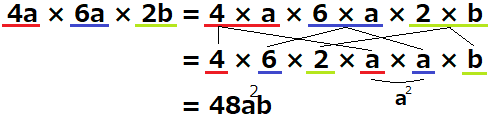
計算前の掛ける項が一つ増えただけなので、前の例題と基本的には同じです!文字同士を掛け合わせる際に同じ文字があった場合は、累乗の形にすることを忘れないでくださいね!
では、次に単項式の除法についても一緒に見ていきましょう!
単項式の除法その①:長方形の辺の長さ
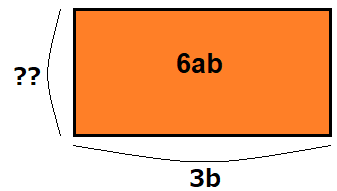
今までの問いと違い、今回は長方形の面積が分かっています。よこの長さもわかっているのですが、たての長さが分からなくなってしまいました。さて、たての長さを求めるには、どのように計算したらよいでしょうか?
乗法の計算でも使いましたが、長方形の面積を求める公式は「面積=たて×よこ」でしたね。面積とよこの長さが分かっているので、たての長さも分かりそうです。

面積の公式を書き換えると「たての長さ=面積÷よこの長さ」となりますね。これを計算していくと分数の形になりますが、乗法と同様に【数字同士、文字同士で計算する】と、答えがでてきます!
単項式の除法その②:文字を含む分数の計算に注意!
次は式だけを挙げていきます!
$$32ab÷\frac{16}{3}a$$
次の問題を解こうと考えるとき、右の分数の項を×の形に変えたいなーと思いますね。割り算の形で分数を計算するのはややこしいのでなるべく避けたいです。では、計算していきましょう!
$$32ab÷\frac{16}{3}a = \frac{32\times{a}\times{b}\times{3}\times{a}}{16}$$
このように分解して、
$$= 6a^{2}b$$
これが答えになります!
と、このように書きましたが、上の式は間違っています。
このように間違える方が多いんです。
一見、合っているように見えるのですが、一体どこが違うでしょうか?
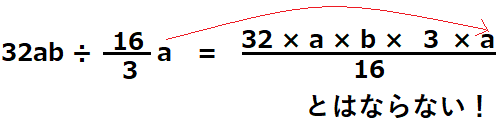
答えは\(a\)の位置です。逆数にしたはずなのに、\(a\)が分子に残ってしまっているんですね。もう少し丁寧に式を書いていけば間違えないはずです。では見ていきましょう。

解き方
- まず、\(÷\)を\(×\)にするために、右の項を逆数に変換します。そうすると、\(a\)が分母に来ることが分かります。分数に掛けられている形というのは、実質、分数の中に分子として入っていると考えると分かりやすいかと思います!
- 次に、分数の形で計算をしていきます。今度は\(a\)が分子と分母に存在しているので、打ち消しあって消えてしまいました。
- 整理すると、答えは\(6b\)となります。
まとめ
単項式の計算は、小学校での計算に文字が加わっただけだと思えば、そこまで難しい事ではないはずです。気を付けることは、繰り返しになりますが、【数字同士、文字同士で計算する】ことです!もし計算が複雑であれば、今回例題で示したように、一度全て分解して計算すると確実に解けるはずです!
やってみよう!
問題
次の問題を解いてみよう。
- \(2x×5y\)
- \(3b×4c×b\)
- \(30ab÷5bc\)
- \(\frac{15a}{2c}÷\frac{5a}{2b}\)
答え
- \(10xy\)
- \(12b^{2}c\)
- \(\frac{6a}{c}\)
- \(\frac{3b}{c}\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。