こんにちは、あすなろスタッフです！
今回は、連立方程式の解き方の一つである、「加減法」を学習していきましょう！
数学が出来ている気がして楽しいと思える人が多い単元の一つが加減法だと思います！一方で、つまづきやすい単元でもあります。
では、今回も頑張っていきましょう！
関連記事：【中2数学】連立方程式とは何だろう…？その意味と解き方について解説します！
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
加減法とは
加減法とは、連立方程式を構成している式同士の足し算・引き算をすることによって、文字の数を減らして、解を探す方法です！最も一般的な方法で、中学校で勉強する方程式のほぼ全てこの方法で解を出すことが可能です。
例題1
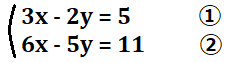
上の式の\(x,y\)を解いてみましょう。
式を見てみると、同じ係数の文字がありません。もしあれば、前回の連立方程式のように、この式そのままで解くことが出来るのですが
さて、計算するためには、一工夫する必要があります。
どちらかの文字の係数が一緒であれば、式の足し算・引き算をすることで、その文字を消去することが出来るのでした。なので、式に値を掛けたり割ったりすることで、係数を合わせてしまえばいいのです！
今回の問題は、\(x\)の係数に合わせていきましょう！なぜ\(x\)にするかというと、3を2倍すれば6になるからです。
\(y\)の係数を等しくしても問題はありません。ですが、2と5の最小公倍数は10なので、両方の式に掛け算をする必要が出てきてしまいます。
説明が長くなってしまいましたが、①式を2倍することによって、\(x\)の係数を等しくしていきます。
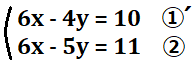
①の式の両辺を2倍した式を①´とします。では、①´と②で式同士の計算をしていきましょう。
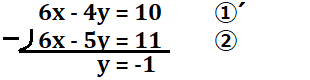
このように、同類項で縦に揃えて、筆算の形にします。では、①´-➁という計算をしていきましょう。
まず、\(6x-6x=0\)ですね。これで\(x\)が消去されました！
次は、\(-4y-(-5y)=y\)となります。符号に注意して計算していきましょう。
最後は右辺の計算ですが、\(10-11=-1\)となります。
これらを式で表すと
$$y=-1$$
となります。これで、\(y\)の解が導出できました！
次は、\(x\)の解ですね。\(x\)の場合は、元の式に\(y\)を代入すれば\(x\)の解が分かります。①式に\(y\)を代入していきましょう。
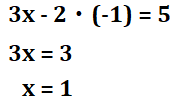
したがって、\(x\)の解は1です。合っているかどうかは、両方の式に\(x\)と\(y\)を入れてみて下さい。どちらも上手く当てはまるはずです。
ちなみに、解はこのように記述します。
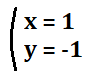
もし学校で別のように教えられたら、学校で教えられたとおりに書いてくださいね。
もう1つ例題を解いていきましょう。
例題2
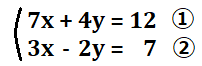
今回は\(y\)の係数を合わせにいくと楽そうです。式②を2倍すれば式①の\(y\)の係数と等しくなるはずです。まず式②を2倍した式②´を作りましょう。
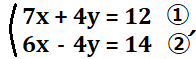
上のような式②´になれば大丈夫です。
では、これを筆算にして、計算していきましょう。
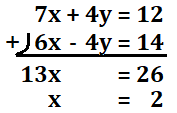
今回は足し算なので、2つの式を足せばいいだけです。計算していくと、
$$x=2$$
だと分かりました！
この\(x\)の値を、式①に代入してみましょう。式②でも式②´に代入しても、解は同じになるので大丈夫です！
計算結果は下の通りです。
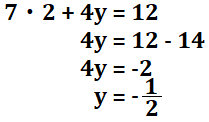
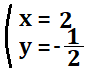
よって、\(y\)の解は\(-1/2\)となります。
まとめ
- どちらかの文字の係数の値を等しくしよう！
- 式の両辺に同じ数を掛けることに注意しよう！
- 筆算では符号間違いに注意しよう！
- 片方の解が求まったら、その解を式に値を代入すればもう一方の解も求まる！
いかがでしたか？加減法を使うと、連立方程式の解の導出が意外とあっさりできてしまいます。慣れてくると、あまり考えなくても解を求めるまでやることが出来るようになると思います。
別の記事で「代入法」という別の方法も紹介しています。こちらも非常にポピュラーな解法なので、是非チェックしてみて下さいね！
やってみよう
次の連立方程式を解いてみよう
1.
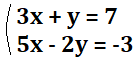
2.
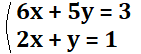
3.
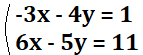
答え
1.
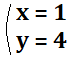
【計算過程】
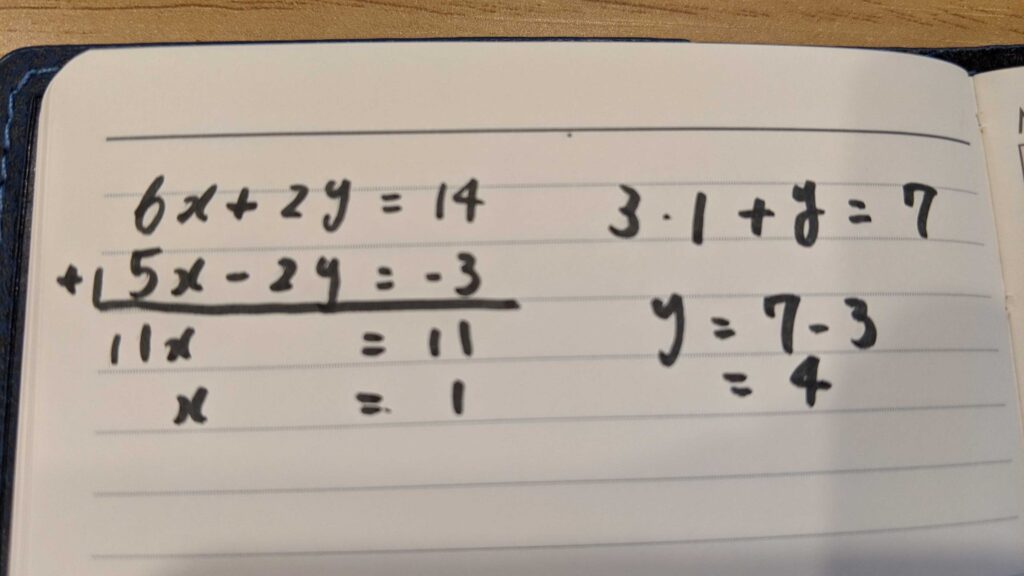
上の式を2倍すると両式の\(y\)の係数が\(2\)に一致する。筆算によって\(y\)を消すことができ、\(x\)の値が\(1\)と求まる。その値を与式に代入することで\(y\)の値も\(4\)と求まる。
2.
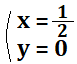
【計算過程】
下の式を3倍すると両式の\(x\)の係数が\(6\)に一致する。筆算によって\(x\)を消すことができ、\(y\)の値が\(0\)と求まる。その値を与式に代入することで\(x\)の値も\(1/2\)と求まる。
3.
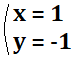
【計算過程】
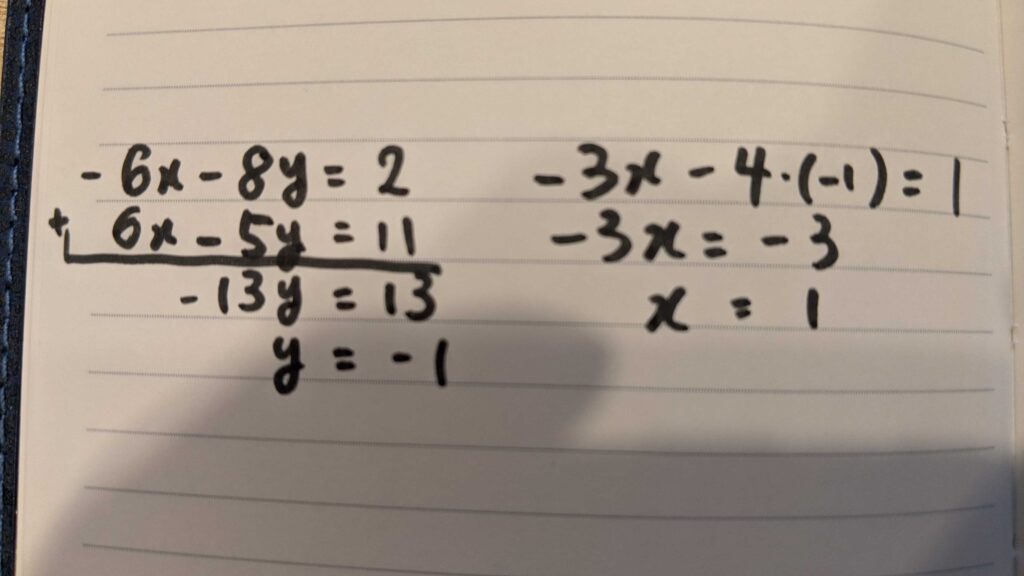
上の式を2倍すると両式の\(x\)の係数が\(6\)に一致する。筆算によって\(x\)を消すことができ、\(y\)の値が\(-1\)と求まる。その値を与式に代入することで\(x\)の値も\(1\)と求まる。
最後までご覧いただきありがとうございました。
｢数学でわからないところがある｣そんな時に役立つのが、勉強お役立ち情報！
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
