【中3数学】根を含む加法の解き方とは？同類項同士で計算する方法について解説します！

こんにちは、あすなろスタッフのカワイです。

今回は、根号を含む式の加法(足し算)・減法(引き算)について解説していきたいと思います！

あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。

参照元：文部科学省　学習指導要領「生きる力」

根号を含む加法とは？

根号を含む乗法・除法では、根の値自体が計算によって変化していました。しかし、加法・減法では項の値は変えないまま、同じ値の根があるときだけ、まとめることが出来ます。

これはどういうことかというと…

例えば、\(\sqrt{3}×\sqrt{7}\)という式があったとします。

これは乗法で勉強したように、根の中の値を計算して、最後に根を付ければいいので、

この解は\(\sqrt{21}\)となります。

一方で、\(\sqrt{3}+\sqrt{7}\)はどのように計算するかというと…

これ以上計算することが出来ません。\(\sqrt{3}+\sqrt{7}\)が解になります。

じゃあ、根号を含む加法って計算すること無いの？

と思うかもしれませんが、同類項があればまとめることで1つの項とすることが出来ます！

例1.式から同類項が見えている場合(\(4\sqrt{3}+7\sqrt{3}\))

\(4\sqrt{3}+7\sqrt{3}\)の場合、\(\sqrt{3}\)という共通した部分があるので、これをまとめることが出来ます。

\(\sqrt{3}\)の部分は\(x\)や\(y\)のようなものと同じように、足し算しても変化しません。

従って、この計算は\(4\sqrt{3}+7\sqrt{3}=11\sqrt{3}\)となります。

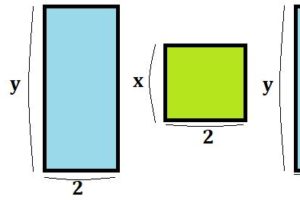
「んー同類項だから一緒にできる？腑に落ちないな…」という人の為に図を用意してみました。

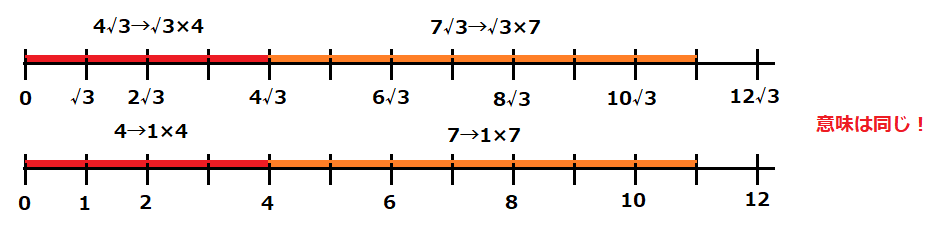
同類項がある加法(足し算)というのは、\(\sqrt{□}\)の部分のある種”尺度”のようになります(定規の目盛りのように、等間隔で並べることが出来ます）。

普段の私たちは、”1”という尺度を用いて計算をしているのであって、そこが\(\sqrt{□}\)に変わっただけなのです。

難しく考えすぎてはいけませんよ！

例2.式からは同類項の存在が確認できない場合(\(\sqrt{2}+\sqrt{8}\))

式から類推出来ない場合、素因数分解ができる値に対して行うことによって、同類項を発見することができれば、例1と同様に計算することが出来ます。

今回の式(\(\sqrt{2}+\sqrt{8}\))の場合、\(\sqrt{8}\)に対して素因数分解をすることが出来ます。では、実際に砕いてみましょう！

\(\sqrt{8}=\sqrt{2×2×2}\)

根の中に同じ値が2つ以上入っている場合、そのうち2つを掛け合わせることで\(sqrt\)を外した形にすることが出来るので、

\(\sqrt{2×2×2}=2\sqrt{2}\)

となります。

おや、\(\sqrt{2}\)が出てきましたね！

同類項が発見できたので、これを例1と同じ要領でまとめることが出来ます。

\(\sqrt{2}+2\sqrt{2}=3\sqrt{2}\)

このように、式を見た時に同類項が無い場合でも、素因数分解によって同類項を探り出すことが出来れば計算できます。

今回の場合、\(\sqrt{2}\)が素数なので良いですが、もし共通項の部分が素因数分解可能であれば、\(\sqrt{}\)の部分を素数にしましょう。

\(\sqrt{2}+\sqrt{5}\)と\(\sqrt{2+5}\)は同じ？

さて、ここまで根の中に1つの数のみ入っているもの同士の計算を行ってきましたが、ここで一つの疑問が生まれます。

\(\sqrt{〇}+\sqrt{□}\)と\(\sqrt{〇+□}\)は等しいのでしょうか？

検証していきましょう。

まず、\(\sqrt{2+5}=\sqrt{7}\)となります。

\(\sqrt{2}+\sqrt{5}\)と\(\sqrt{7}\)という形から類推するのは非常に難しいので、

\(\sqrt{2}=1.414\)、\(\sqrt{5}=2.236\)、\(\sqrt{7}=2.645\)と近似値を用いて計算してみます。

\(\sqrt{2}+\sqrt{5}=1.414+2.236=3.650\)

\(\sqrt{7}=2.645\)

となります。

これらから、\(\sqrt{2}+\sqrt{5}≠\sqrt{7}\)ということになります。

他の値の場合の計算はしませんが、いずれの場合も≠(等しくない)になります。

同類項同士の計算というのが出来ないよ！という事への裏づけになったと思います。

まとめ

• 根を含む加法では、同類項同士の計算を行う！
• もし見当たらない場合は素因数分解で同類項があるか探してみる！

根を含む加法について理解することが出来たでしょうか？もし理解することが出来たなら、後は計算して慣れるのみです！

除法についても同じような具合で計算することが出来ますので、どんどん演習をしていきましょう！

やってみよう！

次の計算をしてみよう。

1. \(3\sqrt{3}+5\sqrt{3}\)
2. \(4\sqrt{7}+3\sqrt{7}\)
3. \(\sqrt{12}+2\sqrt{3}\)
4. \(\sqrt{8}+\sqrt{32}\)

こたえ

1. \(8\sqrt{3}\)
2. \(7\sqrt{7}\)
3. \(4\sqrt{3}\)
4. \(6\sqrt{2}\)

最後までご覧いただきありがとうございました。
｢数学でわからないところがある｣そんな時に役立つのが、勉強お役立ち情報！
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。

もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。