こんにちは、家庭教師のあすなろスタッフのカワイです!
今回は、根を含んだ加法(足し算)・減法(引き算)・乗法(掛け算)・除法(割り算)の計算方法を踏まえ、その応用編である、四則計算を組み合わせた計算について解説していきます。
よく出題されるような問題を何問か解きながら、根のある計算に慣れていきましょう!
根を含む計算について不安がある人向けに、根を含んだ加法・減法・乗法・除法の復習から始めていくので、気楽に最後まで読み進めていってもらえれば幸いです!
では、頑張ってやっていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
【おさらい】根を含んだ加法・減法・乗法・除法
根を含んだ四則計算のそれぞれの公式はこのようになります。
加法
根を含んだ加法は”根の部分の値が等しい”式があるとき、根でない部分を計算することで\(a\sqrt{c}+b\sqrt{c}=(a+b)\sqrt{c}\)という計算が可能です!
もし根が違っても、素因数分解を行うことによって根を等しくすることが出来れば、上のような要領で計算することが出来ます!
例:\(2\sqrt{5}+4\sqrt{5}=6\sqrt{5}\)
減法
根を含んだ減法は加法と同様に”根の部分の値が等しい”式があるとき、根でない部分を計算することで\(a\sqrt{c}-b\sqrt{c}=(a-b)\sqrt{c}\)という計算が可能です!加法の\(+\)の部分が異なる事以外は加法の計算方法と同様です。
例:\(2\sqrt{5}-4\sqrt{5}=-2\sqrt{5}\)
乗法
根を含んだ乗法は、根の中の値同士を”そのまま掛けてあげる”ことで計算が可能です!式で表すと\(\sqrt{a}×\sqrt{b}=\sqrt{ab}\)のようになります。もし根に複数の同じ値の素因数がある場合は、素因数分解をして、根の外に出す操作をします。
例:\(\sqrt{3}×\sqrt{2}=\sqrt{6}\)
除法
根を含んだ除法は、根を含まない除法と同様に、”根の値をそのまま割ってあげる”ことで計算が可能です!式で表すと\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)のようになります。計算した結果、もし分母に根を含む値がある場合は、有理化することによって分母を根を含まない形にすることが出来ます。
例:\(\frac{\sqrt{3}}{\sqrt{2}}=\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{2}\)
より詳しい解説を知りたい方は、それぞれの計算について別記事を用意していますので、そちらを先に読んでみて下さい。
加法:【中3数学】根を含む加法の解き方とは?同類項同士で計算する方法について解説します!
減法:
乗法:【中3数学】平方根を含む乗法(掛け算)のやり方を解説します!
除法:【中3数学】根を含む除法(割り算)・有理化のやり方を解説します!
根を含む「四則計算」計算をしてみよう!
さて、上でおさらいした計算を用いて、これらを複数組み合わせた計算を行っていきたいと思います!
例1.\(\sqrt{12}+\sqrt{27}-\sqrt{48}\)
この問題は、根を含む加法と根を含む減法の2つを含んだ計算になります。加法・減法は\(+\)か\(-\)の違いしかないので、比較的簡単です!では計算手順を記していきましょう。
- 素因数分解を実行し、根の外に出せる値があれば出す。
- 等しい根を持つ項同士を計算する。
まず、\(12\)、\(27\)、\(48\)を素因数分解していきます。
すると、\(12=2^{2}×3\)、\(27=3^{3}\)、\(48=2^{4}×3\)となります。
根の中では2乗部分を根の外に出すことができるので、\(\sqrt{12}=2\sqrt{3}\)、\(\sqrt{27}=3\sqrt{3}\)、\(\sqrt{48}=4\sqrt{3}\)となります。
これらを上式の通りに並べると、
\(2\sqrt{3}+3\sqrt{3}-4\sqrt{3}\)
となります。
今回は偶然すべて同じ根を持つ項が揃ったので、根の外に出ている値を計算すると、
\(2\sqrt{3}+3\sqrt{3}-4\sqrt{3}=\sqrt{3}\)
となります。
例2.\(\sqrt{14}÷\sqrt{8}×\sqrt{10}\)
この問題は、根を含む乗法と根を含む除法の2つを組み合わせた式になります。
この計算手順は、
- 乗法・除法を”根を含まない式と同様に計算する。
- 素因数分解を実行し、根の外に出せる値があれば出す。
- 分母に根がある場合は、有理化する。
まず、これらを計算していきましょう。分数の形でこの式を表すとどうなるかというと、
\(\frac{\sqrt{14}×\sqrt{10}}{\sqrt{8}}\)
となりますね。\(\sqrt{10}\)が分母に来てしまった人は、乗法・除法の計算を見直してみて下さいね。)
さて、これを中身について計算すると、
\(\frac{140}{8}=\frac{35}{2}\)となります。
実際は根が付いているので、\(\frac{\sqrt{35}}{\sqrt{2}}\)となります。
これで完了!としたいところですが、分母に\(\sqrt{2}\)という根があるので、これを有理化します。
\(\frac{\sqrt{35}}{\sqrt{2}}=\frac{\sqrt{35}×\sqrt{2}}{\sqrt{2}×\sqrt{2}}=\frac{\sqrt{70}}{2}\)
となり、計算終了です!
- 式を分数の形にしたときに、掛けるときと割るときでどのように書き表せるのか
- 最後に有理化の確認
と、この2点を抑えれば、ミスを減らすことができます!
例3.\(\sqrt{3}(\sqrt{2}+\sqrt{5})\)
次は、根を含む加法と根を含む乗法を組み合わせた式となっています。
これは、意外にも簡単に解くことができます。計算手順は、
- かっこの中を計算する。(素因数分解をする)
- 乗法をする。(かっこが残る場合は分配法則を用いる)
- 素因数分解をして、根の外に出せる値があれば出す。
という手順になります。文字にして書くと複雑そうに見えますが、そんなことはありません。では解いていきましょう。
まず、()の中を計算していきたいところですが、\(\sqrt{2}\)と\(\sqrt{5}\)は根の値が違うので、加法で計算をすることができません。したがって、分配法則によって、解いていきます。
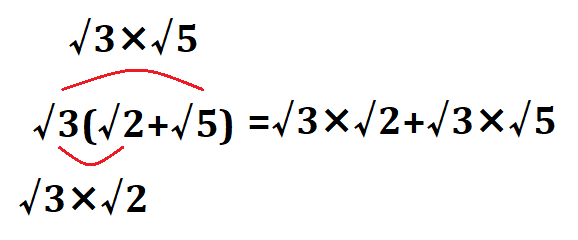
分配法則によって、根を含まない分配法則と同様に、上のような形にする事ができます。
これを計算していくと、
\(=\sqrt{6}+\sqrt{15}\)
となります。\(6=2×3\)、\(15=3×5\)と、どちらの項も同じ値の素因数が2つ以上ないので、これで計算終了となります。
例4.\((\sqrt{18}-\sqrt{8})÷\sqrt{3}\)
最後は、根を含む減法と根を含む除法の組み合わさった式の計算です。計算手順は、
- かっこの中を計算する。(素因数分解をする)
- 除法をする。(かっこが残る場合は分配法則を用いる)
- 素因数分解をして、根の外に出せる値があれば出す。
- 分母に根がある場合は、有理化する。
となり、例3に有理化が加わっただけの違いです。早速解いていきましょう!
まず、\((\sqrt{18}-\sqrt{8})\)ですが、\(\sqrt{18}\)と\(\sqrt{8}\)はそれぞれ\(3\sqrt{2}\)と\(2\sqrt{2}\)となります。これらを見ると、丁度根の値が等しいので、
\(\sqrt{18}-\sqrt{8}=3\sqrt{2}-2\sqrt{2}=\sqrt{2}\)
とすることができますね。そうすると、実際に計算する式は、
\(\frac{\sqrt{2}}{\sqrt{3}}\)
と、簡単な式の形に置き換わってしまいます。
\(2\)も\(3\)も両方素数で素因数分解する必要がありませんが、分母が根になっているので、これを有理化すると、
\(\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{2}×\sqrt{3}}{\sqrt{3}×\sqrt{3}}=\frac{\sqrt{6}}{3}\)
となり、計算完了です!
除法(分数の形の計算式)は最後に大体有理化が必要になりますので、忘れないようにしましょう!
これで例題は以上です。あとは演習問題で計算に慣れていけば完璧です!
まとめ
今回は、少々応用編ということで四則を組み合わせた根の計算をしていきました。どれも基本の「素因数分解」だったり「有理化」という部分が出てくるので、確実にできるようにしていきましょう!
やってみよう!
次の問題を解いてみよう。
- \(\sqrt{18}-\sqrt{32}+\sqrt{50}\)
- \(\sqrt{8}×\sqrt{16}÷\sqrt{6}\)
- \((\sqrt{3}+\sqrt{5})×\sqrt{30}\)
- \((\sqrt{6}-\sqrt{9})÷\sqrt{3}\)
こたえ
- \(4\sqrt{2}\)
- \(\frac{\sqrt{192}}{3}\)
- \(3\sqrt{10}+5\sqrt{6}\)
- \(\sqrt{2}-\sqrt{3}\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。