こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、三角形の合同条件って何だろう?ということについて解説していきます!
合同条件が分かれば、2つの三角形が合同かどうかを数学的に判断することが出来るようになります!
そもそも合同って何だっけ?と思う方でも読み進められるように、合同について復習できる内容を記事内に入れていますので、良ければ最後まで読み進めていってみてください。
それでは今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
【復習】合同とは?
「ピッタリ重ね合わせることが出来る図形の関係」のことを”合同”といいます。
平行移動したり、回転させたり、反転させたりして合わせることができれば、それらは合同です。
形状が同じでも、大きさが少しでも異なる場合、それは合同とは呼びません。
合同の数式での表し方
合同を数字で示すときは、≡の記号で合同な図形の前後を繋ぎます。
例えば、三角形ABCと三角形A’B’C’が合同の場合、
\(三角形ABC≡三角形A’B’C’\)
と示します。
合同の性質
合同な図形は、対応する角や辺の長さは等しいという性質を持っています。
例えば、2つの三角形が合同である場合、対応する「3つの角」と「3つの辺」はすべて等しい
ということになります。これは三角形以外の多角形でも同様なので、
2つのn角形が合同である場合、対応する「nつの角」と「nつの辺」はすべて等しくなります。
三角形の合同条件とは?
さて、合同な三角形は3つの角と3つの辺が等しくなっているという性質があることが分かりました。
では逆に、2つの三角形が合同であると示すためには、その3つの角と3つの辺を全て分かっている必要があるのでしょうか?
実は、そうではないのです。ある辺の数と角の数だけ等しいことが分かっていれば、その図形が合同であると示すことが出来ます。
なぜ全ての角と辺が分からなくても、合同であると示すことが出来るかというと、
三角形の大きさと形が1つに決定できる条件さえ見つけることが出来れば、もう一方と同じ三角形(合同となる三角形)を作ることが出来るからです。
では、等しい辺の数を変えて、三角形の大きさと形が1つに決定できる条件を探していきましょう!
3つの辺が等しい場合
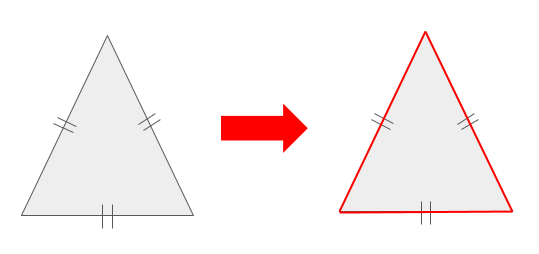
3つの辺が等しいことが分かっていて、1つの角も分かっていない場合、上の図のようになります。
3つの辺が決まっていると、これ以外の形にすることが出来ないので、三角形は1つに決定します。
従って、3つの辺が等しい場合、合同であると言えます。
2つの辺が等しい場合
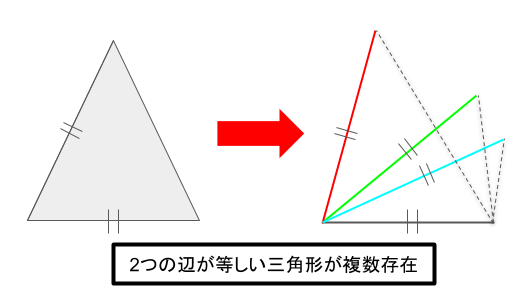
2つの辺が等しいことが分かっていて、1つの角も分かっていない場合、上の図のようになります。
2つの辺によってできる角の角度が自由に決められてしまうので、2つの辺が等しいと分かっているだけでは、1つの三角形に決定することが出来ません。
そこで、その角度を等しいとして固定してあげると、下図のようになります。
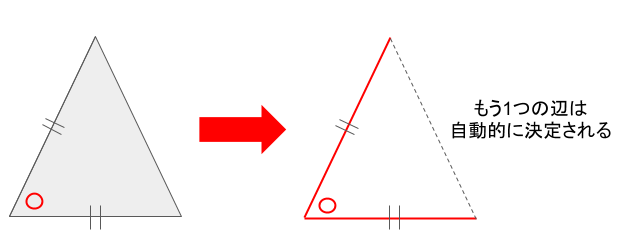
2つの辺が決まっていて、その間の辺も決まっていると、もう1つの辺は一意に決まるので、三角形は1つに決定します。
従って、2つの辺が等しく、その間の角が等しい場合、合同であると言えます。
1つの辺が等しい場合
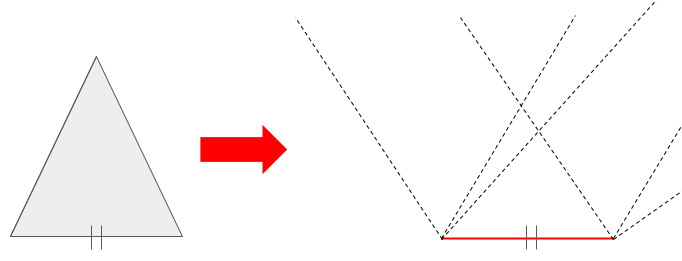
1つの辺が等しいことが分かっていて、1つの角も分かっていない場合、上の図のようになります。
これでは、2辺は決め放題です。三角形が1つどころか、無限に作ることが出来てしまいます。
これでは決まりそうにないので、その辺の片側の1つの角が等しいと分かっている、という条件を追加して考えてみましょう。
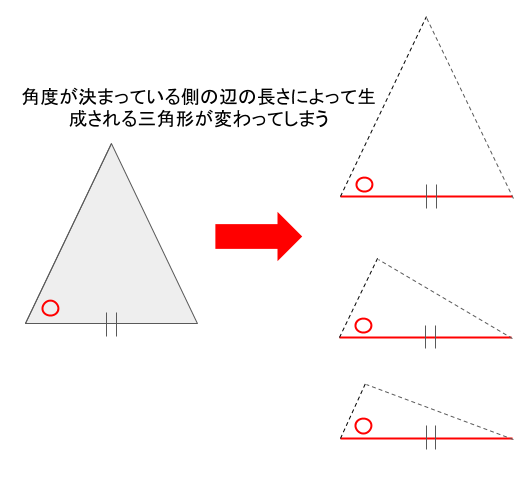
辺と角度が決まると、確かにある程度可能性が絞れますが、角度を決めた側の辺の長さが無限に変えられるので、結局1つの三角形に決定することが出来ません。
従って、その辺の長さを固定してあげれば、1つの三角形に決定できます。これは2つの辺が等しく、その間の角が等しいという、1つ前に説明した合同条件と同じことになります。
今回は、等しいと分かっている辺は1つだけにして、その辺の両側の角(2つの角)が分かっているという条件で考えてみることにします。
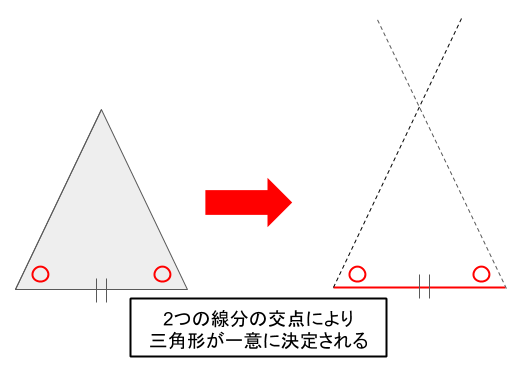
すると、上図のようになります。辺の長さは両側とも決めていませんが、両側から引かれる2つの線分の交点でのみ三角形を成すので、これで辺の長さが固定され、1つの三角形に決定します。
従って、 1つの辺が等しく、その両端の角が等しい場合、合同であると言えます。
まとめ
- 三角形の合同条件は
- 3つの辺が等しい
- 2つの辺が等しく、その間の角が等しい
- 1つの辺が等しく、その両端の角が等しい のいずれかを満たしていることである。
これを図と数式で示すと次のようになります。
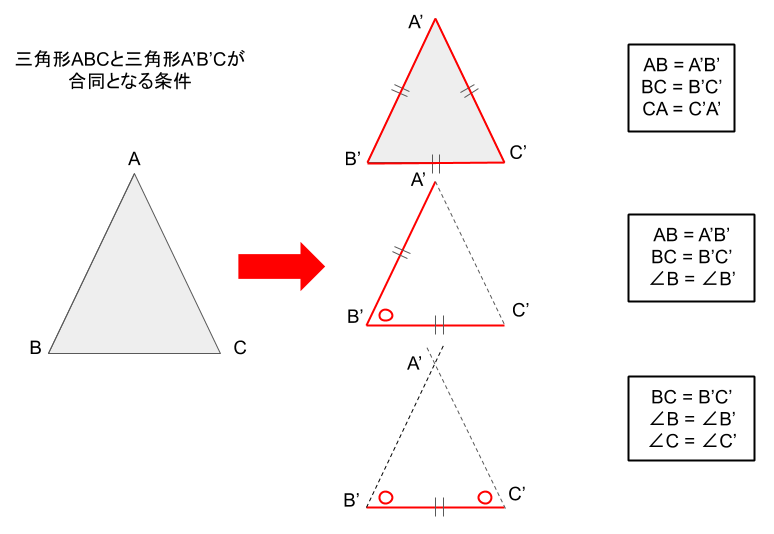
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。