こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、文章中の数量の関係を文字を使って表す方法について解説します!
文字と式の内容が分かっていれば解くことが出来ると思いますが、文章題というだけで苦手に感じる人も結構いると思います。
そのような人たちでも解く事ができるようになるよう解説していきますので、宜しければ最後まで読んでみて下さい!
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。 この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
「文章で表された数量の関係を表す」とは?
文章中の数量の関係を表すとはどのようなことかというと、例えば
“りんごが5個ありました。そこにx個にりんごを増やすと、残りy個となりました。”
といった問題のような、文章で表された数の関係を数式にする、ということです。
上の問題を数式で表すことを考えたときは、「\(5+x=y\)」となります。
問題を考える時の方針は、
- 文章に出てくる値を理解して、
- 「」+「」のような完成形を仮定して、
- 基準・単位に気を付けながら計算して、
- 「」「」に代入して、組み立てる。
です!
今の問題は小学生でも分かるかもしれませんので、中学の単元「文字式」にならった例題を幾つか考えていきましょう。
例題1
”\(100\)gが\(x\)円の肉を\(y\)g買ったとき、その金額は\(500\)円になった。”
上の文章を文字式で表す方法を考えていきましょう。

まず、重さと金額の関係について考えてみましょう。
\(100\)gが\(x\)円ということは、\(200\)g買ったら幾らになるでしょうか。
\(100\)gから\(200\)gへと重さが2倍になっているので、価格も2倍の\(2x\)円になります。
もし\(10\)gなら?\(10\)gは\(100\)gの10分の1の重さなので、\(0.1x\)と表せますね。
では、\(1\)gなら、\(100\)gの100分の1になるので、\(0.01x\)と表せます。
ここから分かるように、金額は、
「基準の重さあたりの金額」×「重さ」=「合計金額」
で表せるということが分かれば、ここに当てはめることで解くことが出来ますね!
では、\(y\)gの場合はどのように表せばいいでしょうか?
ここで気を付ける必要があるのは、「基準の重さ」です!
よくやりがちなのが、
「\(x\)円に\(y\)gを掛けたら500円だから、\(xy=500\)」
ですが、これは間違いです!
なぜなら、\(x\)は\(100\)gあたりというように、\(100\)gを基準としているのに対して、\(y\)は1gが基準になっているからです。
この基準をそろえてあげる必要があります。
なので、今回は\(1\)gの方に合わせてみましょう。
金額は、
「1gあたりの金額」×「重さ」=「合計金額」
となります。さて、\(1\)gあたりの肉の価格というのは、さっき上で表した\(0.01x\)円に他なりません。さて、1gあたりの金額は\(0.01x\)円、重さは\(y\)g、合計金額は\(500\)円なので、上に示したものに代入していくと、
\(0.01x×y=500\)
すなわち、
\(0.01xy=500\)
が正解です。
分数で\(\frac{xy}{100}=500\)としても、意味は同じなので正解です!
このように、基準をそろえる必要がある場合があるので、文章中の「○○あたり~」という文章を見たら注意してみて下さい!
やってみよう!【問題1】
”\(1000\)mlあたり\(a\)円のガソリンがある。これを\(b\)ml買ったら、金額はc円になった。”
これを文字式で表してみよう。
(答えは記事の最後にあります!)
例題2
”家からxkm離れたジムまで時速6kmで歩き、ジムについてすぐにykm離れた駅まで時速10kmで走ったら、1時間かかった。”
つぎはこれを文字式で表してみましょう。
まずは、これをどのように考えればいいのか、頭で思い浮かべていきます。
文章の内容からすると、「家からジム」「ジムから駅」がそれぞれ道のりと速さが決まっていて、
時間については、「家から駅」が決まっています。
(ちょっと分かりにくいので、適当な図で表してみますね。)
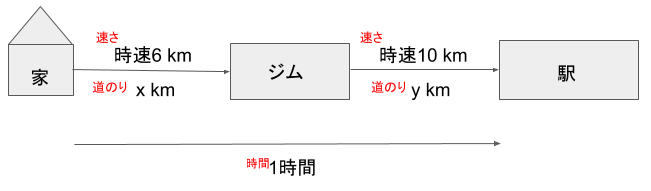
「家から駅まで」という全行程は時間で表されていることから、これを文字式で表すには、「時間」を基準にして、
「家からジムまでの時間」+「ジムから駅までの時間」=「家からジムまでの時間」
という風に表すことを目指して組み立てていきます!
まず、「家からジムまで」の部分を考えていきましょう。
- 道のり:\(x\)km
- 速さ:時速\(6\)km
- 時間:分からない
となっています。ここから時間を求めていきたいですが、
道のりと速さと時間の関係は、
道のり=時間×速さ
で表せるので、時間をa時間としたとき、
\(x=6×a\)
なので、
\(a=\frac{x}{6}\)
と表されます。
ということで、「家からジムまでの時間」は\(\frac{x}{6}\)時間
と分かりました。
小学校の時に
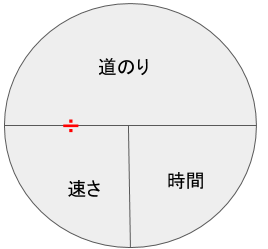
のような図で習った人は、これで考えても大丈夫です。
次に、「ジムから駅までの時間」について考えていきましょう。
これは「家からジムまでの時間」の時と考え方は全く同じです!
- 道のり:\(y\)km
- 速さ:時速\(10\)km
- 時間:分からない
となっているので、時間を\(b\)時間とすると、道のりと速さと時間の関係より、
\(y=10×b\)
\(b=\frac{y}{10}\)
となります。
したがって、「ジムから駅までの時間」は\(\frac{y}{10}\)時間
と分かりました。
さて、ピースはすべてそろったので、これを組み立てると、
「家からジムまでの時間」+「ジムから駅までの時間」=「家からジムまでの時間」
より、
\(\frac{x}{6}+\frac{y}{10}=1\)
となれば完成です!
この問題も、先ほどの問題と同じように、基準を見つける事が大切です。
また、今回の問題は大丈夫でしたが、単位が違う場合は単位をそろえる必要もあります。
その点に注意して、次の問題を解いてみて下さい!
やってみよう!【問題2】
”A地点から\(x\)m離れたB地点まで分速60mで歩き、B地点から\(y\)m離れたC地点まで分速100mで早歩きで進んだら、1時間かかった。”
この文章を文字式で表してみよう。
(答えは記事の最後にあります!)
例題3
”あるレストランの昨日の客は\(x\)人で、今日の客は昨日より\(y\)%増えて\(120\)人になった。”
これを文字式で表してみましょう。
まず、今わかっている事と、分からないことを図で表してみます。
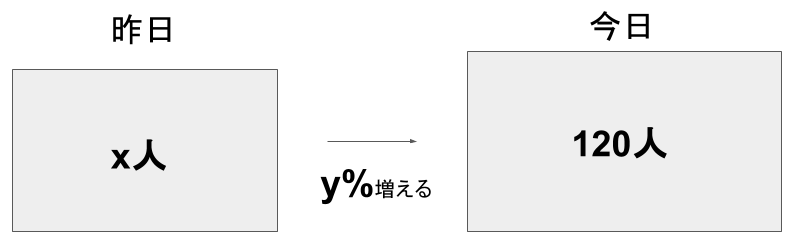
こんな感じになりますね。
従って、これは「昨日の客の数」×「増加割合」=「今日の客の数」
という式で考えられます。
%について考えてみる
%というのは、「元の値から100分の〇だけ変化する」ということを表したものです。
仮に1%客が増えるとすると、その変化分は
「\(+\frac{1}{100}\)」×「もとの数(\(x\))」
と表せるので、\(frac{1}{100}x\)となります。
したがって、変化後の合計人数は
\(x+\frac{1}{100}x\)
\(=\frac{101}{100}x\)
と表すことが出来ます。
ということは、「\(y\)%増加」とは「もとの値から100分の\(y\)だけ増える」ということなので、
昨日の客の数\(x\)を用いて、今日の人数(昨日の客+\(y\)%)を考えると、
\(x+\frac{y}{100}x=\frac{100+y}{100}x\)
と表せます。
さて、これは今日の客の人数(\(120\)人)と一致する必要があるので、
\(\frac{100+y}{100}x=120\)
となり、これが完成です!
%の意味を理解しておけば、こんな問題もこのように文字式に表すことが出来ちゃいます!
やってみよう!【問題3】
”あるレストランの昨日の客は\(x\)人で、今日の客は昨日より\(y\)%減って\(z\)人になった。”
この文章を文字式で表してみよう。
(答えは記事の最後にあります!)
まとめ
「文字式の完成形を想像して、分からない部分を作って、組み立てる。」
このプロセスを踏めば、大体の文字式の問題を解くことが出来るはずです。
分からない問題があった時は、「割合」や「道のり・速さ・時間」「個数と値段の関係」など、小学校の頃に勉強した内容を復習して、解けるようになりましょう!
答え
- \(\frac{ab}{1000}=c\)
- \(\frac{x}{60}+\frac{y}{100}=60\)
- \(\frac{100-y}{100}x=z\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。