【中1数学】反比例のグラフや座標が分かっているときの、式の導き方を解説します！

こんにちは、あすなろスタッフのカワイです。

今回は、反比例のグラフから式を導出する方法や、比例定数が分からない時の式を導出する方法を解説したいと思います。

あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。

文部科学省　学習指導要領「生きる力」

http://www.mext.go.jp/a_menu/shotou/new-cs/index.htm

グラフが分かっている時の式の求め方

例1.この反比例のグラフの式を求めなさい。

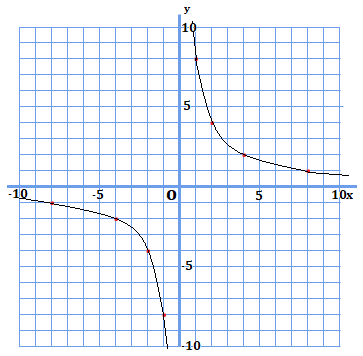
比例のグラフが示されていて、比例定数が分からない時、どのように式を導出すればよいでしょうか。

これは意外と簡単です。

反比例の式は

$$y=\frac{a}{x}$$

と表されます。したがって、これを式変形すると

$$xy=a$$

となります。従って、グラフ上の1点が分かれば、比例定数を導くことが出来ます。

そもそも、このグラフとは？

余談なので、早く答えを知りたい方は飛ばしてください！

この反比例のグラフは、式の意味の通り、\(x×y\)がある一定の値になる位置になるように打たれています。従って、

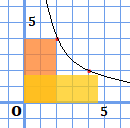
原点Oと線の通っているところの2点によってできる四角形の面積は、曲線上のどこをとっても等しくなります。

この考え方は、今後数学を勉強している時に使う場合があるので、もし余裕があれば覚えてみてください！

さて、話を戻します。

グラフの1点\((x,y)\)が分かれば、式を導出することが出来ます。今回のグラフでは、\((2,4)\)や\((1,8)\)のところに点が打たれています。従って、この\(x=2\)と\(y=4\)を式\(xy=a\)に代入すると、

$$2×4=a$$

$$a=8$$

と計算でき、比例定数は\(8\)だと分かりました！

従って、このグラフで示された式は

$$y=\frac{8}{x}$$

です。

このような問題の場合、\((1,8)\)など、曲線上の他の点でも当然同じ比例定数が出るので、どの点を取って計算してみても全く問題ありません。もし本当かどうか気になる方は、ほかの点で同じ式が本当に導かれるのか、計算してみてください！

反比例の一点が分かっている時の式の求め方

例2.\(y\)は\(x\)に反比例し、\(x=3\)のとき、\(y=-4\)である。\(y\)を\(x\)で表せ。

次は、反比例の関数の1点が分かっていて、比例定数が分からない時の式の求め方について解説します。

この問題も、\(xy=a\)の考え方を用いれば問題ありません。

この式より、

$$3×-4=a$$

$$a=-12$$

となるので、反比例の式は

$$y=-\frac{12}{x}$$

となります。

以上です。簡単ですよね。

問題自体はこれで解けてしまったわけですが、理解を深める為に、この式のグラフを考えてみましょう。

\(y=-\frac{12}{x}\)を表で表すと、

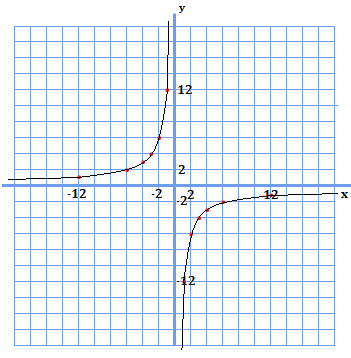
となります。当然ですが、確かに\((3,-4)\)を通っていますね。

このグラフを作成すると、

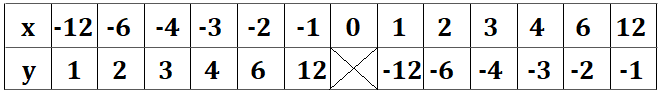
上のように図示されます。当然ながら、\(x\)と\(y\)の積が\(-12\)となる点を繋いだものとなっています。従って、反比例であることが分かっていて、1点の座標が分かってさえいれば、(\(O\)を除く)どの点であっても反比例の式・グラフを示すことが可能です。

まとめ

いかがでしたか。今回は、グラフや点から反比例の式・グラフを導く方法を解説しました。\(y=\frac{a}{x}\)の式を変形して、\(xy=a\)となることが分かっていれば、そこから比例定数を導出して、式やグラフを示すことが出来る、という流れが理解できたのであれば、今回はOKです。

次回は、これまでに解説してきた「比例」「反比例」を実際に利用して、どのような場合にどのように学んだことを生かすことが出来るのか、考えながら解くことが出来るように、解説していきたいと思います。

やってみよう

1.次の反比例のグラフから、比例定数と式を示してみよう。

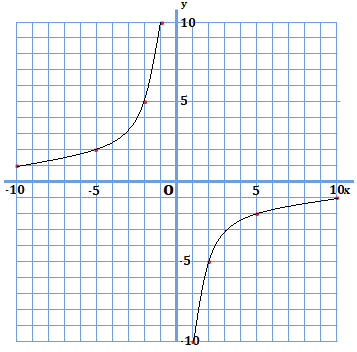
2.\(y\)は\(x\)に反比例し、\(x=-2\)のとき、\(y=-6\)である。\(y\)を\(x\)で表してみよう。

こたえ

1. 比例定数：\(a=-10\)、式：\(y=-10x\)
   (解説)：まず、\((x,y)\)が互いに整数となっている点のうち1点を読み取る(例として\((-1,10)\)をとる)。反比例の式\(y=\frac{a}{x}\)に\(x=-1\)、\(y=10\)をそれぞれ代入すると、\(a=-10\)となる。これを\(y=\frac{a}{x}\)の式に代入すると、式は\(y=-10x\)となる。
2. \(y=12x\)
   (解説)：\(y\)は\(x\)に反比例しているので、式は\(y=\frac{a}{x}\)となる。これに\(x=-2\)、\(y=-6\)をそれぞれ代入すると、\(a=12\)となる。これを\(y=\frac{a}{x}\)の式に代入すると、式は\(y=12x\)となる。

最後までご覧いただきありがとうございました。
｢数学でわからないところがある｣そんな時に役立つのが、勉強お役立ち情報！
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。

もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。